Abstract

正则流（Normalizing flows）提供了一种通用的机制来定义富有表达力的概率分布，只需要指定一个（通常简单的）基础分布和一系列可逆变换。

Intraduction

正则流通过将简单的密度通过一系列变换来产生更丰富、可能更多模态的分布，就像液体流经一组管道一样运作。
灵活性意味着正则流非常适合用于建模、推断和模拟这些关键的统计任务。
我们对正则流的探索旨在揭示那些将指导它们在可预见的未来进行构建和应用的持久原则。
Section 2: 建立正则流的形式和概念结构。
Section 3 ：有限正则流结构(finite)；Section 4：极微小变体（infinitesimal variant）。

Section 2：正则流（Normalizing Flow）

2.1 定义和基础

规定 x 是 D 维的真实向量，流模型的主要思想是使用从 $p_u(u)$ 中采样的真实向量u通过变换T表达x。

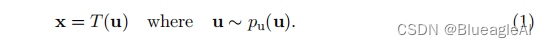
我们规定 $p_u(u)$ 是流模型的基本分布。用参数{φ, ψ}分别表示T与 $p_u(u)$ ，也就引出了由{φ, ψ}定义在x上的分布组。

流模型的基本属性是T必须可逆，T与 $T^{-1}$ 可微，由此也可以推得：

等价的，可以得到：

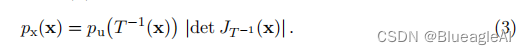
雅可比矩阵（Jacobian）为：
在这里插入图片描述

在实践中，我们通常用神经网络构建T，并且选取一个简单的密度函数，如多元正态分布，来构建 $p_u(u)$ 。在Section 3和4中会讨论如何实施(implement) T。
我们可以将变换T看作是对空间R^D的扭曲，以将密度函数pu(u)塑造成px(x)。绝对雅可比行列式|det JT(u)|量化了由于T引起的u周围小邻域的体积相对变化。简单来说，假设du是u周围的（无限小的）小邻域，dx是du映射到的x周围的小邻域。我们可以得到 $det J_T(u)| ≈ Vol(dx)/Vol(du)$ ，即dx的体积除以du的体积。dx中的概率质量必须等于du中的概率质量。因此，如果du被扩展，那么x处的密度将小于u处的密度。如果du被压缩，那么x处的密度将较大。
可逆且可微分的变换的一个重要性质是它们是可组合的。给定两个这样的变换T1和T2，它们的复合变换T2 ◦ T1 也是可逆且可微分的。它的逆变换和雅可比行列式可以表示为：
因此，我们可以通过组合多个更简单的转换实例来构建复杂的转换，而不影响可逆性和可微性的要求，因此也不会失去计算密度 $p_x (x)$ 的能力。所以"flow"指的是从 $p_u(u)$ 中获得一组样本，在经过 $T_1,...,T_k$ 的变换序列时所遵循的轨迹。术语"Normalizing"指的是通过逆变化 $T^{-1}_1,...,T^{-1}_k$ 的流动，将 $p_x(x)$ 中获得的一组样本转化为预定密度$p_u(u)的一组样本（某种意义上为正则化）。
在功能上，基于流的模型提供了两个操作：通过公式1从模型中进行抽样，以及通过公式3评估模型的密度。这些操作具有不同的计算要求。从模型中进行抽样需要能够从 $p_u(u)$ 中进行抽样，并计算正向变换T。评估模型的密度需要计算逆变换 $T^{-1}$ 及其雅可比行列式，并评估 $p_u(u)$ 的密度。具体应用将决定需要实施哪些操作以及它们需要多高的效率。我们在Section 3和Section 4讨论了与各种实现选择相关的计算折衷。

2.2 流模型的表达能力

在研究流的细节之前，重要的问题是：How expressive are flow-based models? Can they represent any distribution $p_x(x)$ , even if the base distribution is restricted to be simple?
我们将证明，在 $p_x(x)$ 满足合理条件的情况下，这种通用表示是可能的。具体来说，我们将证明，对于任何一对良好行为的分布 $p_x(x)$ （目标分布）和 $p_u(u)$ （基础分布），存在一个可微分同胚能够将 $p_u(u)$ 转化为 $p_x(x)$ 。这个论证是构造性的，并基于Hyvärinen和Pajunen（1999）关于非线性独立成分分析（ICA）存在性的类似证明；更详细的处理可以参考Bogachev等人的研究（2005）。
具体证明过程可以看论文，比较长这里就不赘述了。