文章目录
- Story so far
- 形式逻辑
- 命题 proposition
- 谓词 predicate
- 连接词
- Variables
- Set 集合
- Set operation 集合操作
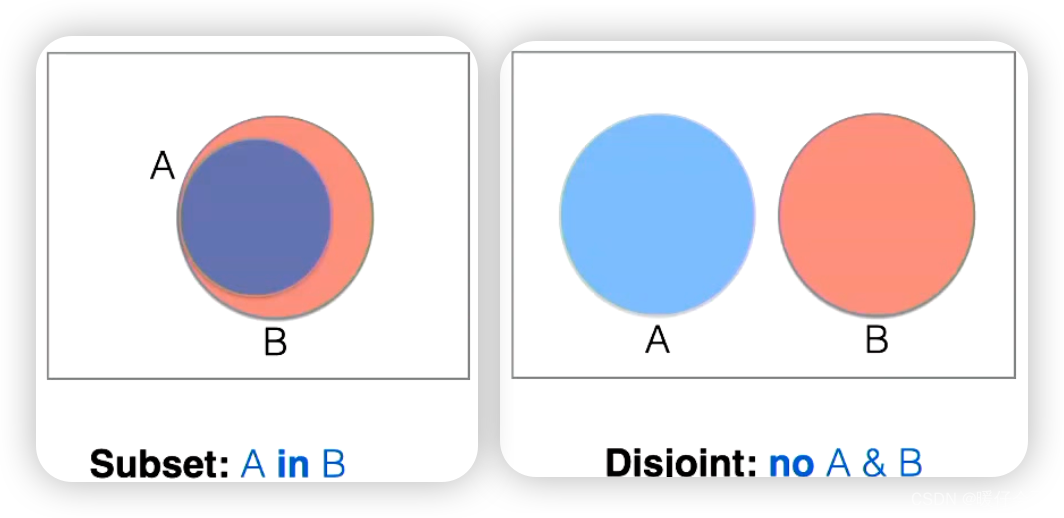
- Set Relationship 集合关系
- Alloy Set alloy 的集合表示
- Quantification 量词
- Relations 关系
- 案例
- Binary Relations 二元关系图
- Functions 函数
- Total v.s. Partial Function
- Relation Operation 关系操作
- add
- update
- restriction
- relation joins
- function call 函数调用
Story so far

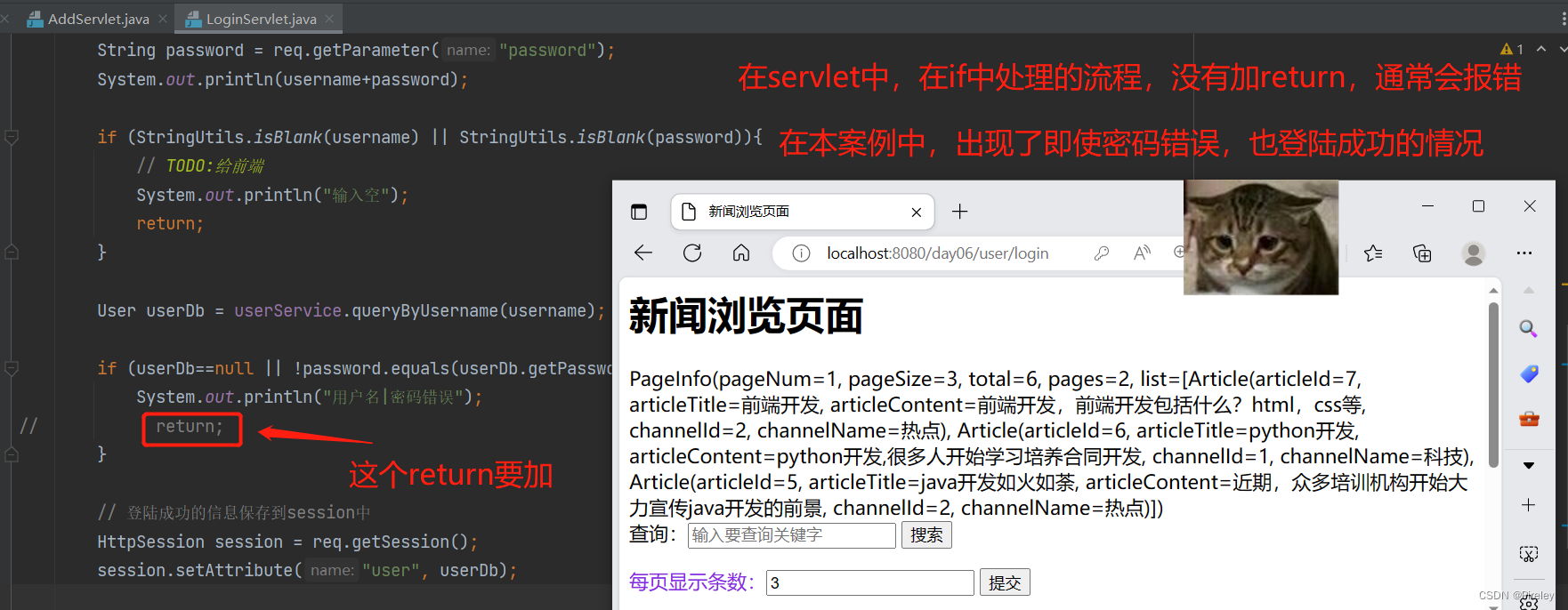
在软件工程生命周期的 Design 阶段,使用一种形式化规范的方法,通过逻辑推理来检查系统的设计是否满足需求,并确保这些需求得到保证。他们提到了一个基于模型的规范风格,称之为形式化规范。这种规范使用逻辑来书写系统的需求和设计,并使用逻辑推理来检查系统设计是否满足这些需求。演讲者提到,为了简化逻辑推理的过程,他们将使用一个外部工具来完成这个任务。

为了更好地理解形式化规范的概念,讲者介绍了一种简单而强大的逻辑——一阶集合论 / 谓词逻辑,并解释了如何使用这种逻辑来写下规范,并通过逻辑推理来验证规范是否满足要求。他还提到,为了实现这些规范,将使用一种名为Alloy的工具,它可以帮助我们理解规范的含义,并验证规范中的某些属性是否成立。
形式逻辑
我们要讨论的是一些相对简单的概念,但我们会尽可能地精确,包括命题集合、谓词和关系。我们还会谈到我们对这些概念的理解或见解。在介绍这些普通概念(如集合和关系等)的同时,我还会试图给你们展示这些概念在Alloy中的应用。我将努力保持一致性,用蓝色字体表示Alloy理解的内容及其符号。
命题 proposition
首先,什么是命题呢?命题在逻辑中是最基础的东西。逻辑主要讨论的是事物的真假。所以,命题就是你能在逻辑中写下的最基本的陈述,它是真的,还是假的。例如,"现在正在下雨"就是一个命题。这是一个可能为真也可能为假的陈述。这个命题显然是相对于现在的时间和我们所在的地点的。我想我们都同意,除非我们进入大楼后天气发生了巨变,否则现在这里应该没有下雨。所以,这个命题现在是假的。

- 那么在
alloy中,我们就用Raining来表示这个 命题 - 这个词在Alloy中有一个特殊的名称,它被称为
Atom。在后续的内容中,我们将了解如何定义这些原子。但现在,你可以将raining这个词视为一个原子命题,它要么是真,要么是假。
谓词 predicate
-
但是,我们可能想要更具体一些。我们可能想要说出它在哪里下雨。这就是一个命题:
在Parkville正在下雨。在Alloy中,我们可能会写成Raining[Parkville]。在Alloy中,当你用参数调用一个函数或谓词时,几乎总是要用方括号。

-
所以在第二个例子的
raining中,不是一个单一的事物,它既可以为真也可以为假。我们可以将它视为一个函数,它接受一个参数(在这个例子中,是一个地点Parkville)并根据在Parkville是否下雨来返回真或假。 -
现在,这个函数本身有一个特殊的名称,它被称为谓词。所以,谓词基本上就是接受一个参数的命题,然后返回真或假。或者,一个谓词可能接受多个参数,然后根据命题的类型返回真或假。

连接词
-
当然,我们可能想要写下更复杂的命题,例如连接其他命题的命题,或者复合语句(compound proposition)。例如:“在Parkville正在下雨,而在Sydney却没有下雨”。为了做到这一点,我们需要一些方法来组合我们的命题,以构建更大的命题。

-
所以,我们有所谓的逻辑连词,用于将命题连接在一起,形成更大的命题。
- 我们可以将两个命题连接在一起,表示它们都必须为真,这就是逻辑与(and)。
- 我们也可以将两个命题连接在一起,表示其中一个必须为真,这就是逻辑或(or)。
- 我们还可以表示一个命题必须为假,这就是非(not)或否定。
- 我们可以表示,如果一个命题为真,那么另一个命题也必须为真,这就是蕴含(implies)或逻辑蕴含。
- 我们还可以表示两个命题必须同时为真,这就是当且仅当(iff),也就是它们必须具有相同的值。或者等价地,我们可以说它们必须互相蕴含。
-
在Alloy中,我们写下这些内容时,我们将使用左边这一列的符号,如
and、or、not、implies、iff等。
有了这些工具,我们当然可以构建更大的命题,例如:在Parkville正在下雨,而在Sydney没有下雨。或者我们可以写下像 raining[Parkville] implies not raining[Sydney] 这样的语句。那么,这意味着什么呢?
对,如果在Parkville下雨,那就意味着在Sydney没有下雨。这就是你应该如何理解蕴含的含义。
到目前为止,我们讨论的都非常简单,只是一些非常基础的逻辑语句,比如在Parkville下雨或者下雨。
Variables
当然,在你的系统规范或对你的系统及其期望特性的逻辑描述中,你在写下这些内容时,你需要能够引用系统状态的不同部分。对此,我们有变量。我们在编程语言中有变量,所以在逻辑中有变量不应该让人感到惊讶。
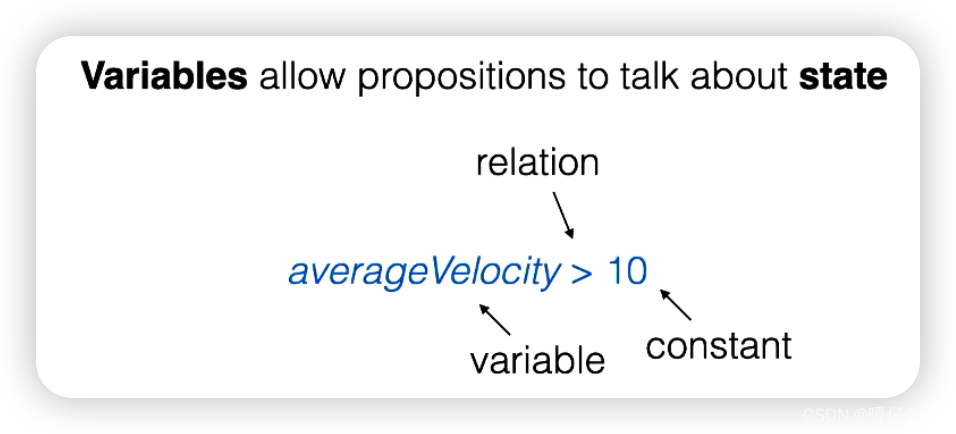
例如,我们可能有一个描述系统中平均速度的变量,我们可能想要说它大于10。这是我们可能想要写下的非常简单的命题。你可以看到,这不仅引用了一个变量,而且还引用了一个常数,即数字10, 显然,这是一个 relation,即 > 关系。 > 就是一个关系,你给它两个数,它会告诉你第一个数是否比第二个数大。你给它两个数,它会返回真或假,取决于第一个数是否比第二个数大。这预示了我稍后会告诉你的一件事,即关系就是谓词。但是,我们稍后再回到这个问题。

所以,我们可以说诸如 averageVelocity > 10 and currentVelocity = 11 之类的事情。
现在,当我们在我们的形式化规范中使用变量时,我们所做的是描述我们希望我们的系统如何行为,或者我们希望我们的系统具有哪些特性,而这些变量将被用来引用状态的不同部分。 但这是在我们的逻辑模型中的状态,而不一定是我们用逻辑描述的系统或程序的实际状态。

例如,averageVelocity 可能不会在真实系统中存在,比如如果这是在模拟一辆车的电子自动刹车系统,那么在那个电子控制单元中可能没有一个叫做 averageVelocity 的变量。相反,averageVelocity 可能只存在于我们的规范中,可能是指最近的n个速度变量值的总和除以n。所以,重点是,我们可以在我们的模型或规范中有一些在真实系统中不存在的东西,但是仍然允许我们谈论我们希望真实系统具有的真实系统的特性。
Set 集合

Alloy中的一个重要概念是集合。事实上,在Alloy中,所有的东西都是集合,所有的东西都是关系,而这两者实际上是一样的。 所以,集合将是非常重要的。集合就是一组事物的集合,我们可以用大括号将元素围起来,或者我们可以用所谓的集合推导式来描述一个集合,比如 “所有偶数x的集合”。这就是一些基础的逻辑概念和Alloy的概念。
Alloy 提供了一些特殊的集合供我们讨论:
- 全集(universal set,Alloy 中表示为
univ) - 空集(empty set,Alloy 中表示为
none)
Set operation 集合操作
当然,我们可以开始讨论集合运算,如 A 集合和 B 集合中的所有元素(Alloy 中用 + 表示),或者既在 A 集合又在 B 集合中的所有元素。我们还可以讨论在 B 集合中但不在 A 集合中的所有元素。如果你曾经接触过集合论,你应该会知道这三个操作就是标准的 并集、交集和差集。Alloy 是以方便键盘输入为目标设计的符号系统,因此并集 +、交集 & 和差集 - 的表示方法都是键盘友好的。在传统的数学符号系统中,这些操作通常分别表示为 ∪, ∩, \。这个方便的设计在你实际写 Alloy 的时候会很有帮助。
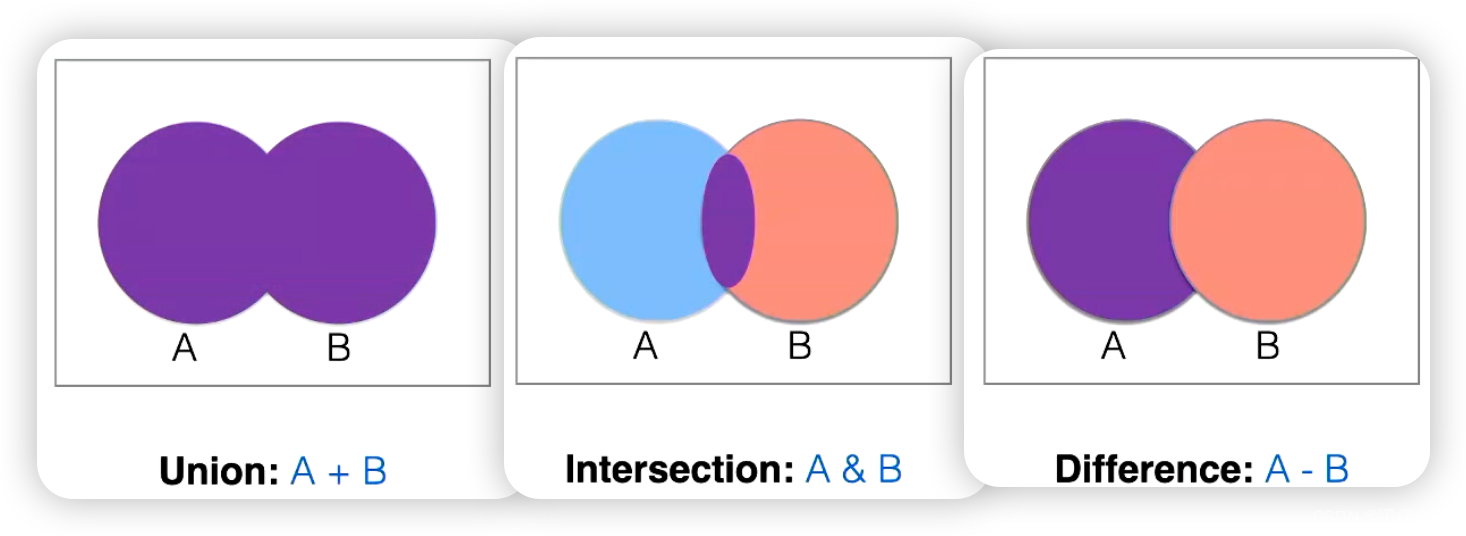
Set Relationship 集合关系
Alloy Set alloy 的集合表示

x in A和B in A其实没有本质的区别,因为在 alloy 中所有的东西都是集合,其实x in A不过是{x} in A即,只包含一个元素的集合{x}属于集合A3其实就表示{3},即使是一个元素,在 alloy 中也代表一个集合#A在 alloy 中是获取集合元素个数的操作
Quantification 量词
这部分将讨论逻辑定量词,并将其与集合、谓词和关系相联系。
首先,让我们从逻辑定量词说起。例如,我们可以说 “P 对所有的 x 都成立”,或者我们可以说 “不存在一个 x 使得 P 不成立”,或者 “不存在一个 x,使得 P 的否定为真”。在逻辑和 Alloy 中,我们可以这样表示 “非存在某个 x 使得非 P(X)”。

同样的原理也适用于存在量词。
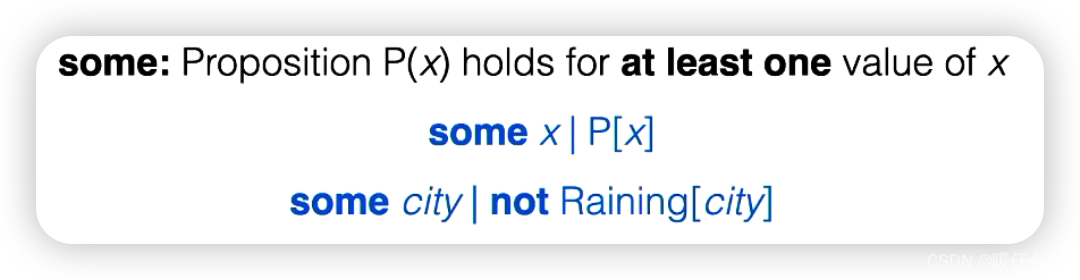

Alloy 为了方便使用,有时会提供一些额外的量词,你可以根据我们已经看到的内容来定义它们。例如,你可能想说 存在某个 X 使得 P(X) 成立,但你可能想明确表达的是,这对于 X 的某一个值是真的,Alloy 为此提供了一个特别的量词 one。或者你可能想说 P 对于最多一个 X 的值成立,Alloy 为此提供了一个 lone 量词。**记住这个量词的方法是,它表示 P 对于 X 的值小于或等于一个成立,即 “less than or equal to one”,**即 “l one”。当然,你也可以表示没有任何 X 的值使得 P 成立,即 “none x | P[x]”。
Relations 关系

我曾经说过我们将学习 集合、谓词和关系,并暗示所有这些事物实际上都是一样的。Relation 本质上就是 谓词,你给它们一些参数(通常是一或两个),它们根据这个关系是否成立返回真或假。比如我们之前看到的 > 关系,如果我们将它视为一个接受两个参数(比如6和5)的函数,那么 “大于” 会返回真,因为6大于5。但如果我们给它的参数是2和3,它会返回假,因为2不大于3。
我们将 Relation 视为返回真或假的谓词。一个 relation 的元(arity)就是它需要的参数数量。我们看到的如 “大于” 这样的**关系是二元关系,因为它需要两个参数。**但你也可以有一元关系,只需要一个参数就可以返回真或假,或者你可以有接受多个参数的关系,然后返回真或假。
谓词和关系通常被用来定义集合。例如,集合 { x ∈ Z | x > 0 } 是所有正整数的集合。这个集合的定义包含一个谓词 “x > 0”,这个谓词描述了集合中元素的性质。只有那些满足这个谓词的元素才会被包含在集合中。
然而,Alloy并不直接支持这种方式定义集合。Alloy是基于关系的模型,因此在Alloy中,我们构建 relation 是基于元组:

- 在这个例子中,
Sum表示的是一个三元的关系,每一个三元关系中,都包含三个变量x,y,z,这个Sumrelation 当然也是一个集合。 - 简化来说,
relation就是tuple的集合
案例

- 在这个例子中,我们首先定义了一个
relationFactor,也就是说对于Factor中的每个项,都是一个包含(x,y,z)的元组,其中x = y * z - 接下来我们的任务是定义一个
predicate,当我们把(x,y,z)放到这个predicate中的时候,如果是prime,那么就会返回true - 由于我们已经得到了关系
Factor,而prime的定义是: 一个大于1的自然数,除了1和它自身外,不能被其他自然数整除的数叫做质数。 - 在这个例子中,我们首先针对一组
(x, y, z)因为x = y * z所以这时候y和z的值就变成了是否让x成为prime的关键。因此我们将这个isPrime的谓词逻辑定义为:all y, z | (x,y,z) in Factor implies y=1 or z=1或者也可以写成all y, z | Factor(x,y,z) implies y=1 or z=1

- 从本质上来看
relation,predicates以及sets都是一样的
Binary Relations 二元关系图
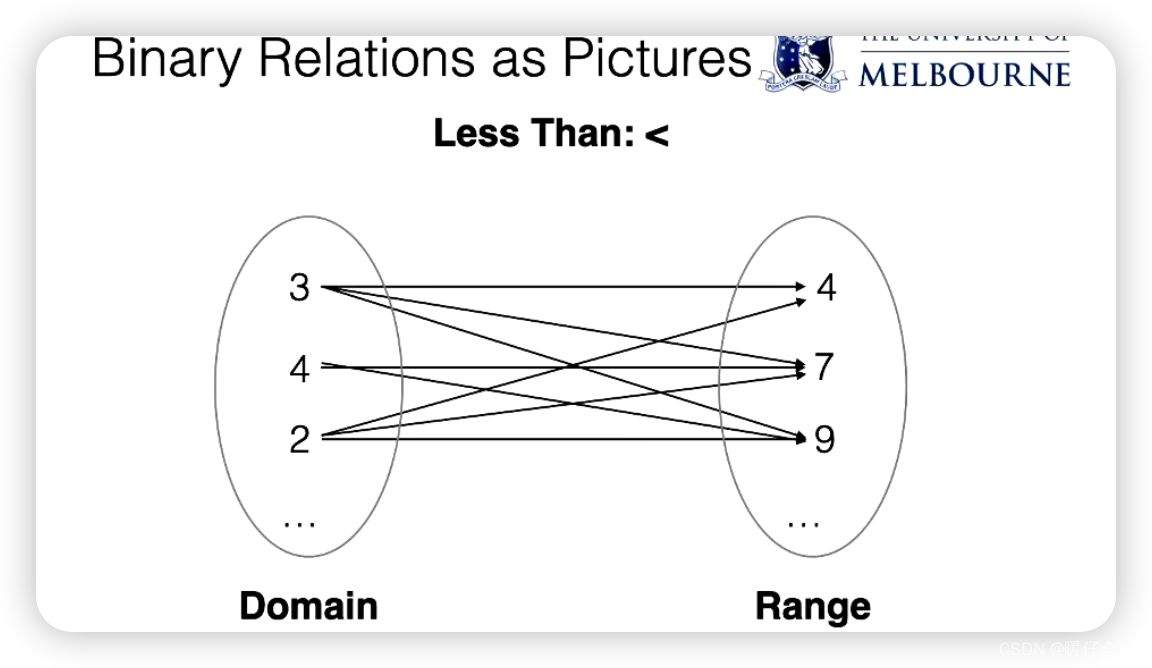
- 图中表示了
<这种relation,这是一种二元关系,在二元关系中,我们定义一个domain一个range,即定义域和值域,例如:从 3 指向 4 的箭头3 -> 4表示了在这个关系中3 < 4

- 在数学中,我们通常会用形式化的方法来表示两个
set之间的relation - 例如,我们现在有一个
set:username,其中包含了username_1, .... username_n,还有一个password集合,其中包含pass_1,....,pass_m, 那么如果我们有一个数据库 LDAP,代表username -> password的关系,那么我们可以表示LDAPDB为LDAPDB一定是username与password笛卡尔积组成的集合的一个子集,即LDAPDB⊂ \subset ⊂username × password
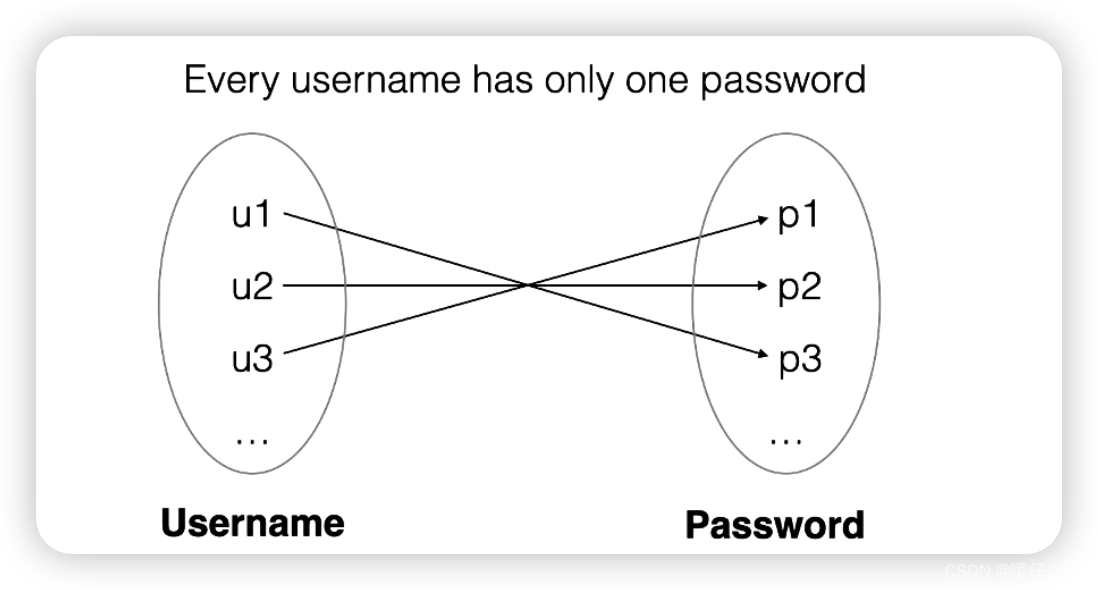
Functions 函数
- 如果每个 username 只对应一个 password, 那么这种关系可以看做函数
function
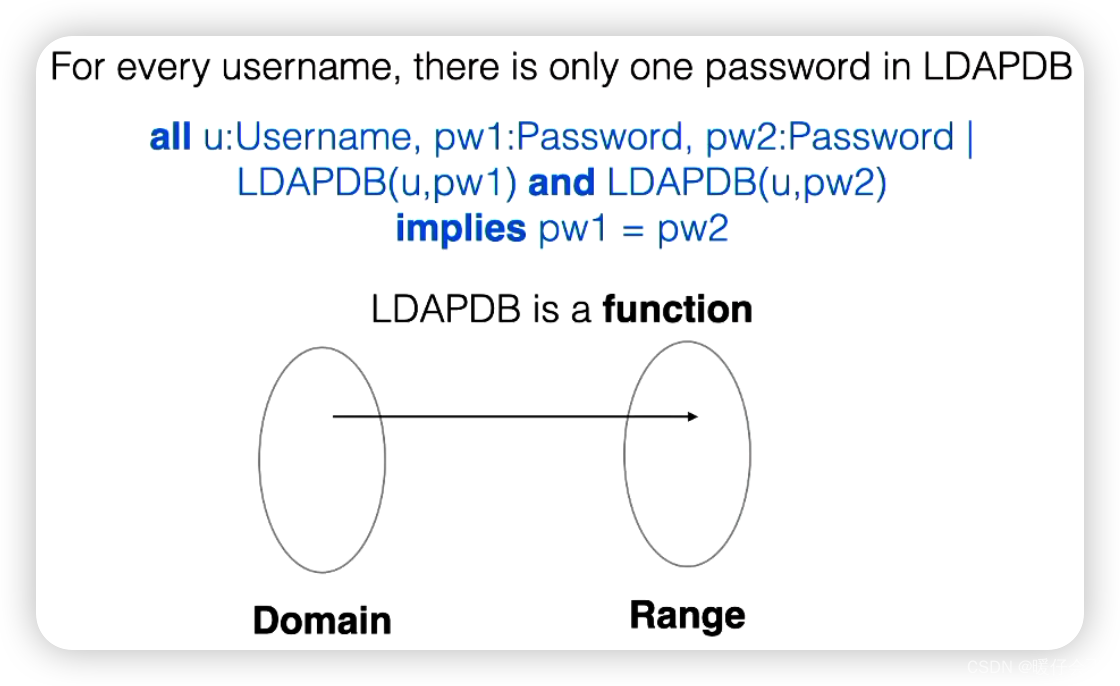
Total v.s. Partial Function
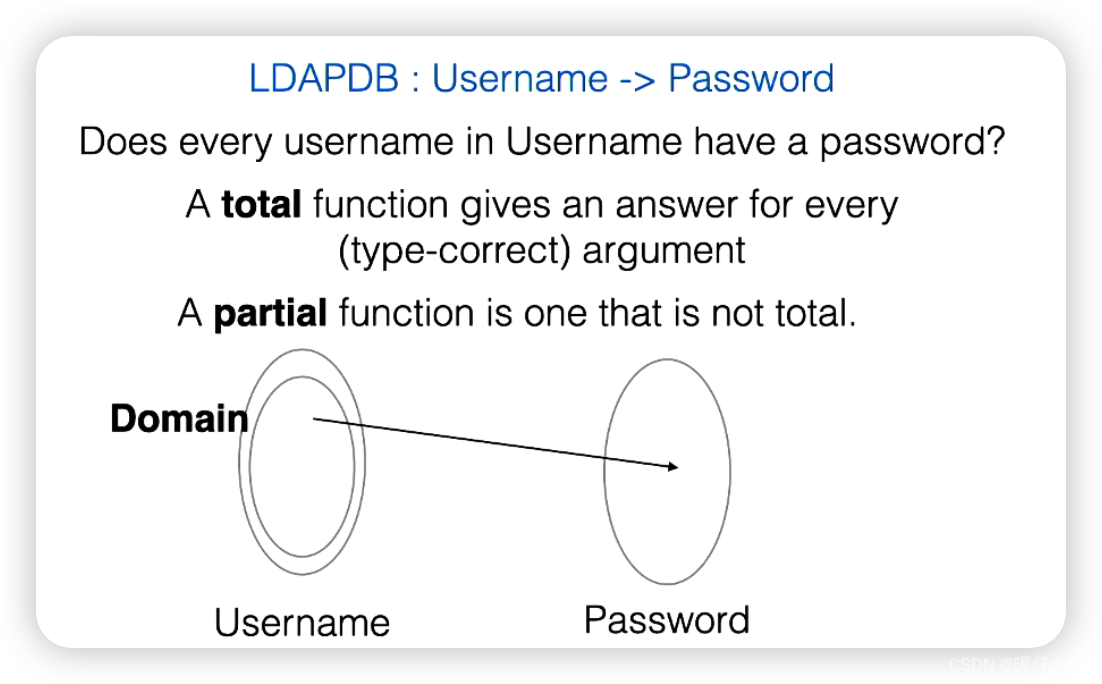
partial function就是给定一个username,未必会对应一个passwordtotal function则是一一对应的关系
Relation Operation 关系操作
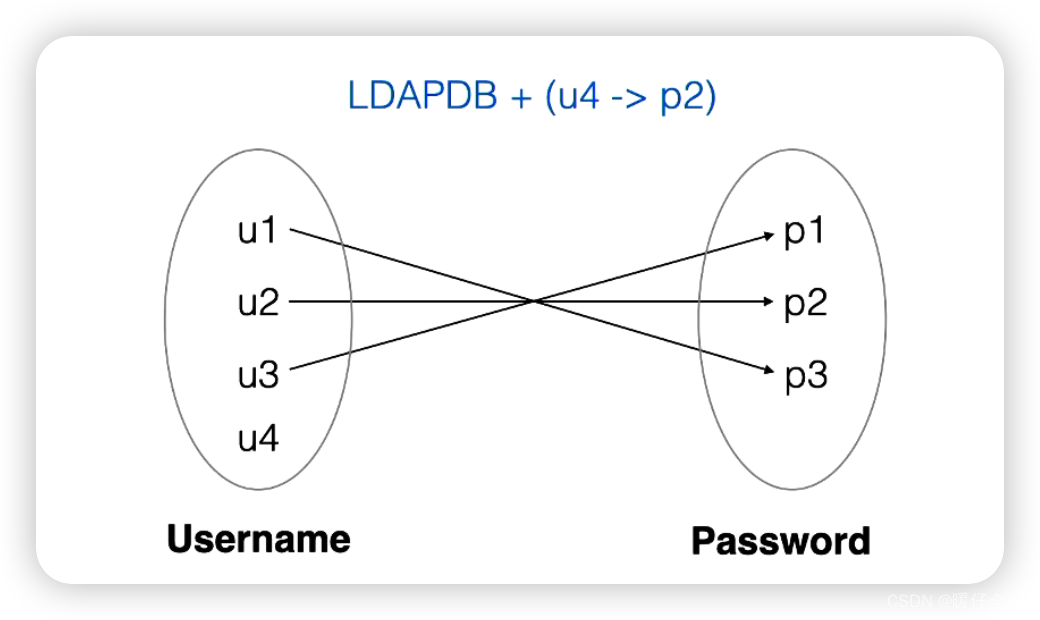
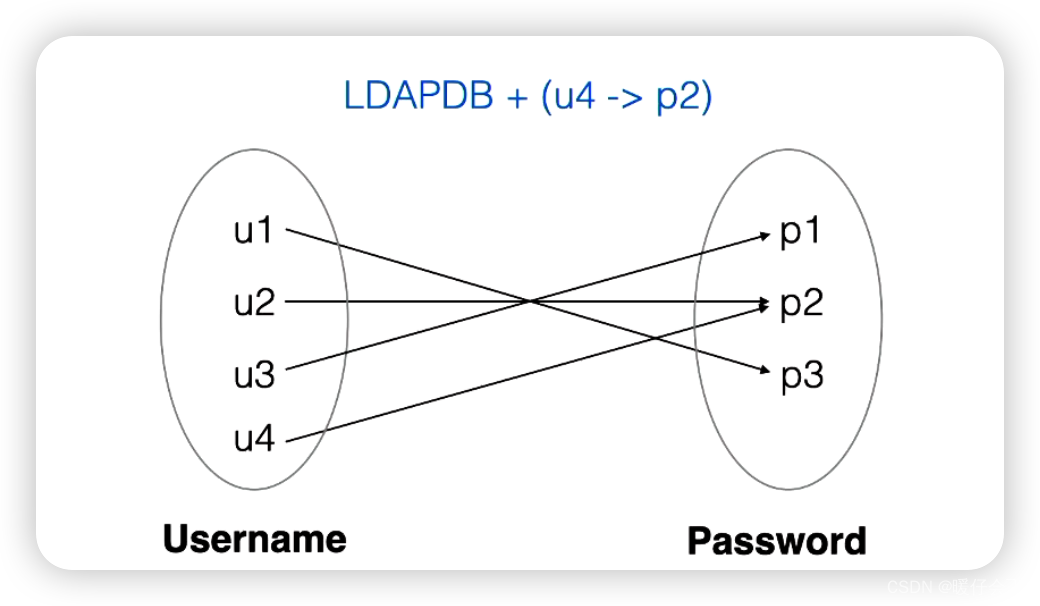
add
- 当我们已经拥有一组关系
relation: A -> B,那么我们可以通过+这个操作符来扩展这个relation,如图所示,我们在relation中增加了一个新的关系(u4->p2)
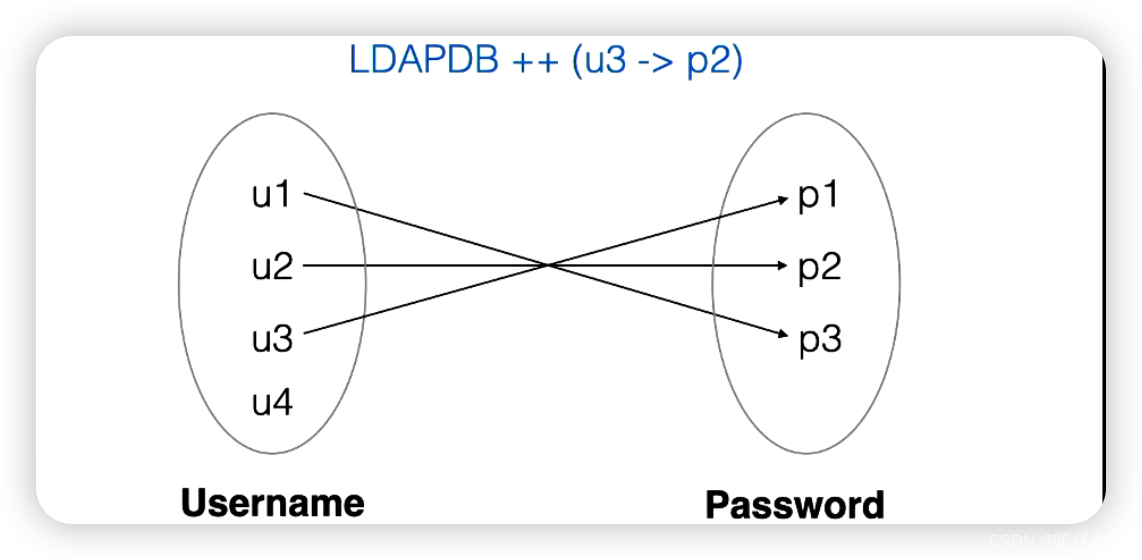
update
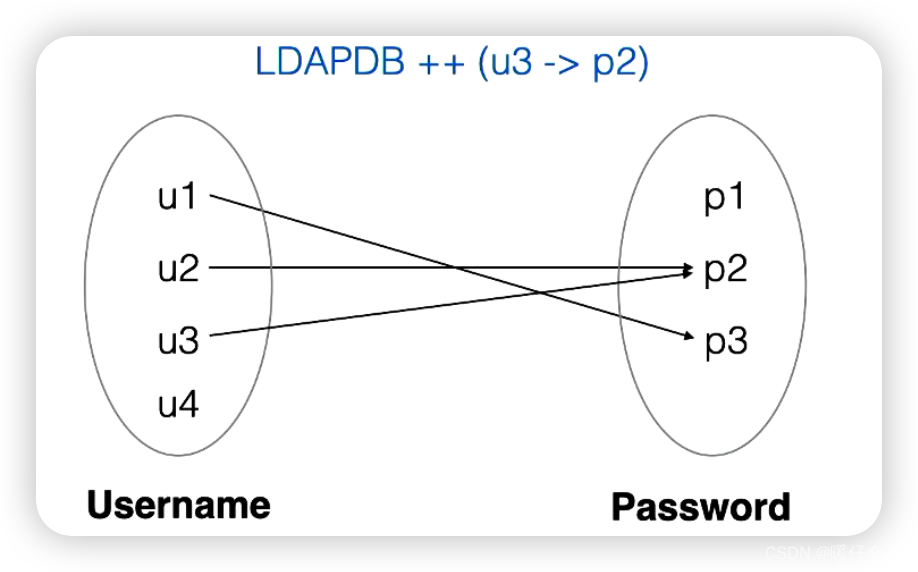
restriction
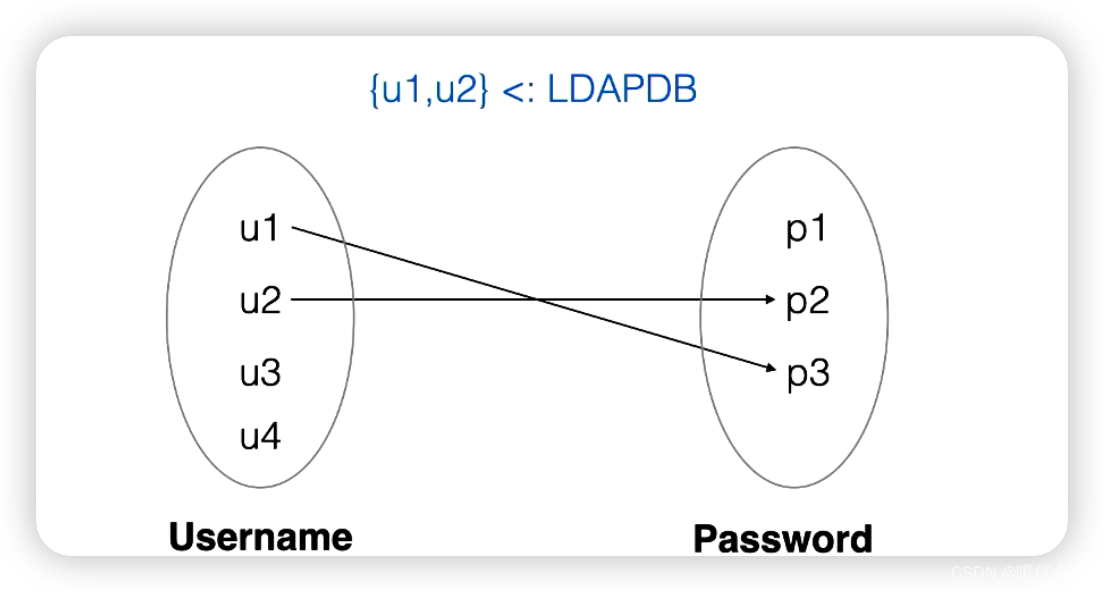
- 符号
<:表示,只关心当前relation中的u1 和 u2,其他的不管,有点类似于filter操作 - 这个符号不仅可以用于
domain,还可以用于range端
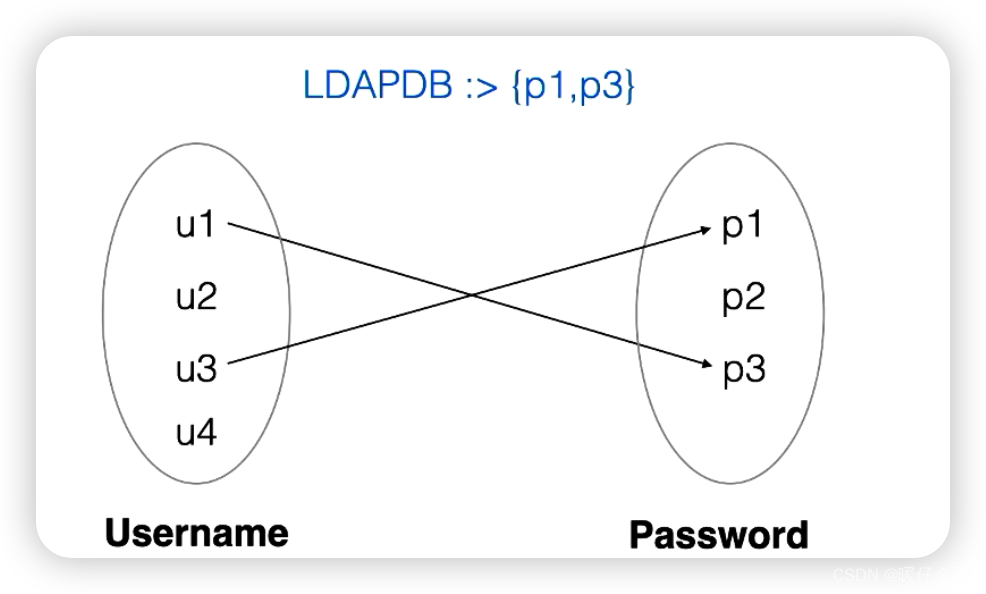
- 这样的写法表示,我们只关心
{p1, p3},而不关心password中包含的其他内容
relation joins
A.B代表join操作

- 拿第一个 A 中的
(0,1)举例子,它的最后一个位置的1与 B 中的(1,1,1)的第一个位置的1相同,因此他们可以join,join之后的结果表现为A.B=(0,1,1)因为他们共同的1被合并了,同样的,后面以此类推 A.B还可以表示为B[A]:

function call 函数调用

我们已经知道了几点知识:
- 函数
f是一组关系,包含了 (a1, b1), … (a_i, b_i) 的总共i个元组,由于f构建的是A->B的映射关系,因此我们可以写成A->B join操作可以表示为A.B等价于B[A]
那么针对上述的知识,如果我们调用函数 f 并将 a_i 作为参数传入,会得到什么结果呢?
- 首先
a_i相当于{a_i},所以f[a_i] = {a_i}.f也就是集合{a_i}与整个关系f的join操作 - 那么结果显而易见就是
(a_i)只能匹配到(a_i, b_i)并进行联合,而共同的a_i被消掉了,因此最终的结果是b_i也可以认为是{b_i}