✳️ 一、引言

图像是一种表达信息的形式，其中，数字图像反馈的信息更加丰富。在获取图像的过程中，图像的形成、传输、存储、处理过程受到外界干扰或成像设备自身的局限等多种因素，导致获取的图像质量不高，使图像分辨率下降，这种情况称为降质或退化，具体表现为图像模糊、有噪声、分辨率下降、图像失真、振铃波纹、边缘信息丢失或产生马赛克等质量下降等现象，这给处理图像和后续应用带来很大影响。由于造成图像质量下降的因素有很多，例如：空气流动造成摄影设备晃动、摄影设备移动中模糊，设备像素不高、光学系统差别、成像设备局限性以及频谱混叠等，因此，图像质量下降的原因没有办法从根本上解决。

✳️ 二、图像复原基本原理

图像复原是利用对退化图像的先验知识以及对其退化过程的研究，来尽量重建或复原退化的图像，得到原图像的最佳估计图像。因此，图像复原可以看成是沿着图像降质过程反方向处理的逆过程，是对图像降质过程加以分析和估计，建立相应的图像退化的数学模型，尽量消除退化过程造成的失真情况，以此方式获得未经退化的原始图像或原始图像的最优估计，从而达到提高图像质量的目的。

图像复原是根据图像的退化成因，通过图像处理技术尽量地去除或减少在获得观测图像过程中产生的降质影响，因为使图像降质的原因很多，不便一一建模分析，所以通常用统一基础数学模型对图像的模糊过程进行描述。在图像复原过程中，高分辨率图像可以用f(n1, n2)表示，其中n1，n2＝0，1，2，…，N-1。相应的低分辨率图像则为g(m1, m 2)，其中m1，m2＝0，1，2，…，M-1。其中M=N/R，R是f(n1, n2)和 g(m1, m 2)采样率。在不考虑模糊噪声的情况下，高分辨率图像和低分辨率图像的关系可用以下模型表示：

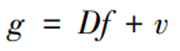
在这里插入图片描述

其中，f为按照字典序排列的未知高分辨率图像向量，g为按照字典序排列的拍摄时所获取的已降质的低分辨率图像向量，v则是相应的噪声值向量。根据字典序准则，向量g和向量v分别为 ${{M}^{2}}\times 1$ 维的矩阵，f为 ${{N}^{2}}\times 1$ 维矩阵。矩阵Ｄ在此则表示在高分辨率图像和低分辨率图像的转换过程中的降采样及滤波矩阵，为 ${{M}^{2}}\times {{N}^{2}}$ 矩阵

✳️ 三、正则化插值原理

正则化理论由 Tikhonov和 Miller提出，为采用正则化方法解决不适定性问题提供了一个基本的解决思路，其中基于稳定函数(stabilizing functional)方法是最基本的方法。根据此方法，一个不适定性问题可以转化稳定函数的约東最小化问题此方法的约東取決于使用稳定函数的形式和性质，且这些约東与期望正则解的先验知识有关。

根据正则化方法，图像插值的解

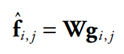
在这里插入图片描述

可通过对代价函数最小化得到：

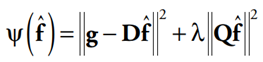
在这里插入图片描述

式中：Q为二维的正则化算子；λ为正则化参数。

最小化操作可通过对代价函数求导实现:

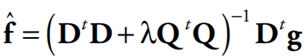
在这里插入图片描述
即有：

在这里插入图片描述

正则化算子Q的作用是使D的小特征值不为零，而大特征值不变，且考虑了插值过程中涉及的f平滑度的先验知识。

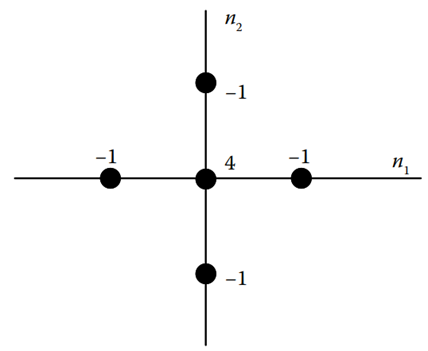
正则化算子Q用来最小化估计图像的二阶或更高阶差分能量，为有限差分知阵。图1所示的二维拉普拉斯算子是最常用的最小二阶差分能量的正则化算子，本博文采用此算子。正则化参数λ用来平衡解的失真度和平滑性之间的关系。

在这里插入图片描述

图1 二维拉普拉斯算子

以前，正则化理论主要应用于基于迭代的图像复原或频域场合。目前，正则化方法被应用到图像插值。然而，在频域中求解不现实，而其迭代计算可以表为

在这里插入图片描述

式中:fi为第i次迭代得到的高分辨率图像；为收敛参数。

此方法是有效避免了矩阵求逆的大计算量，但其缺点似乎需要大量的迭代计算以获得较好HR图像效果。

✳️ 四、实验验证

在模拟实验中，首先对原始图像进行降采样，然后加入高斯白噪声(AWGN)来模拟低分辨率图像降质模型，最后，对低分辨率图像进行双线性插值重构原始图像，结果如图2所示，此时，重构图像与原始图像之间的峰值信噪比为21.8820。

在这里插入图片描述

图2 正则化插值重构结果

✳️ 五、参考文献

[1] S. E. El-Khamy, M. M. Hadhoud, M. I. Dessouky et al. 2005. Efficient Implementation of Image Interpolation as an Inverse Problem, J. Digital Signal Proc., 15, 137–152