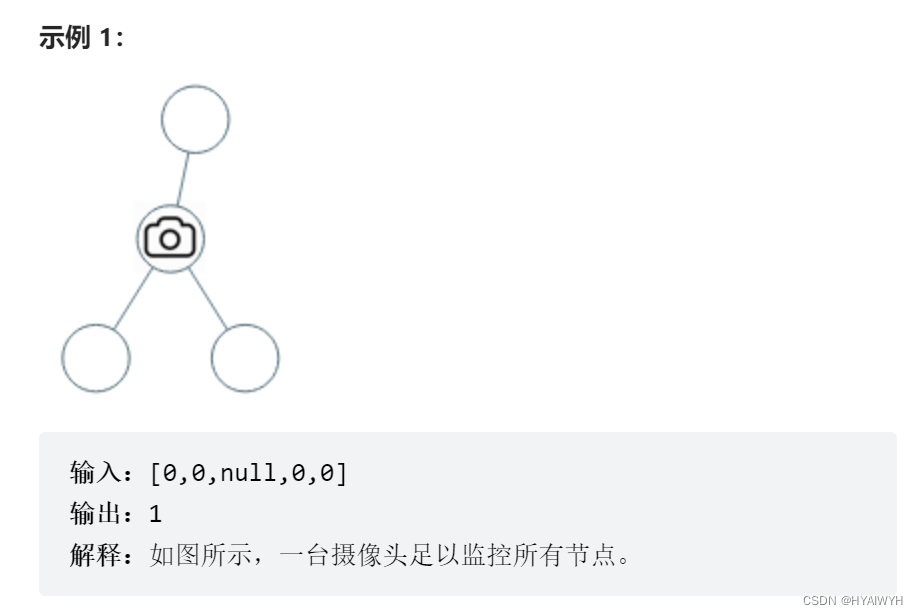
给定一个二叉树，我们在树的节点上安装摄像头。

节点上的每个摄影头都可以监视其父对象、自身及其直接子对象。

计算监控树的所有节点所需的最小摄像头数量。

---

思路：

        1、要尽可能的少安装摄像头，那么摄像头不可能安装在叶子节点上，从叶子节点开始从下往上遍历，用左右中的后序遍历方式；

        2、每个节点有3种状态，无覆盖、有摄像头、有覆盖，分别设为0、1、2；

        3、确定好遍历顺序后，终止条件，如果遇到空节点，则默认为有覆盖；

        4、单层逻辑：对左右孩子的状态进行判断，来确定父节点的状态

        主要分成了4种情况：(1)左右孩子均为有覆盖，父节点为无覆盖情况；

                                          (2)左右孩子只要有一个无覆盖，则需要在父节点加一个摄像头；

                                          (3)左右孩子只有有一个摄像头，则父节点就为有覆盖情况；

                                          (4)最后需要对根结点进行判断，如果无覆盖，则需要再加一个摄像头。

class Solution {
private:
    int result;
public:
    int traversal(TreeNode* root){
        //终止条件
        if(root==NULL)  return 2;
        //遍历顺序：左右中 后序遍历
        int left=traversal(root->left);
        int right=traversal(root->right);
        //中
        if(left==2&&right==2)   return 0;//左右孩子均为有覆盖，父节点为无覆盖情况
        if(left==0||right==0)
        {
            result++;
            return 1;//左右孩子只要有一个无覆盖，则需要在父节点加一个摄像头
        }   
        if(left==1||right==1)   return 2;//左右孩子只有有一个摄像头，则父节点就为有覆盖情况
        return -1;//不会走到这一步
    }
    int minCameraCover(TreeNode* root) {
        result=0;
        //对根结点进行判断，如果无覆盖，则需要再加一个摄像头
        if(traversal(root)==0)  result++;
        return result;
    }
};