系列文章目录

第二章：K近邻（分类）

相关代码地址：https://github.com/wzybmw888/MachineLearning.git

---

---

一、最近邻算法

为了判定未知样本的类别，以全部训练样本作为代表点，计算未知样本与所有训练样本的距离，并以最近邻者的类别作为决策未知样本类别的唯一依据。

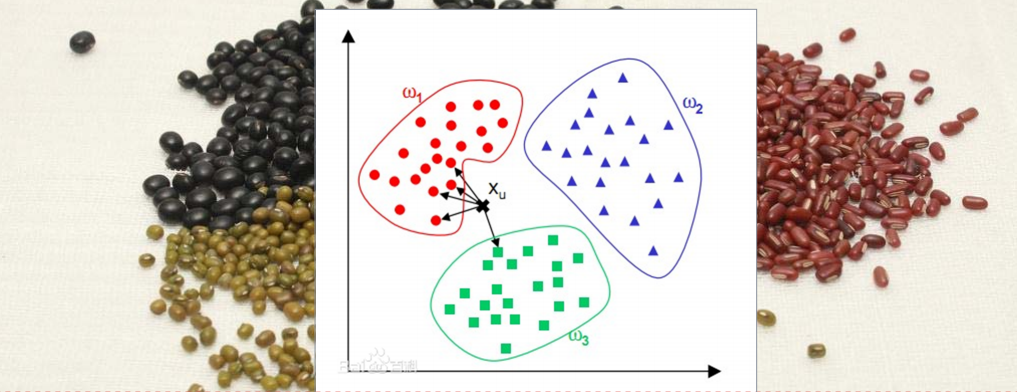
那么如何计算位置样本与所有训练样本的距离呢？在sklearn中提供了如下计算距离的类方法：

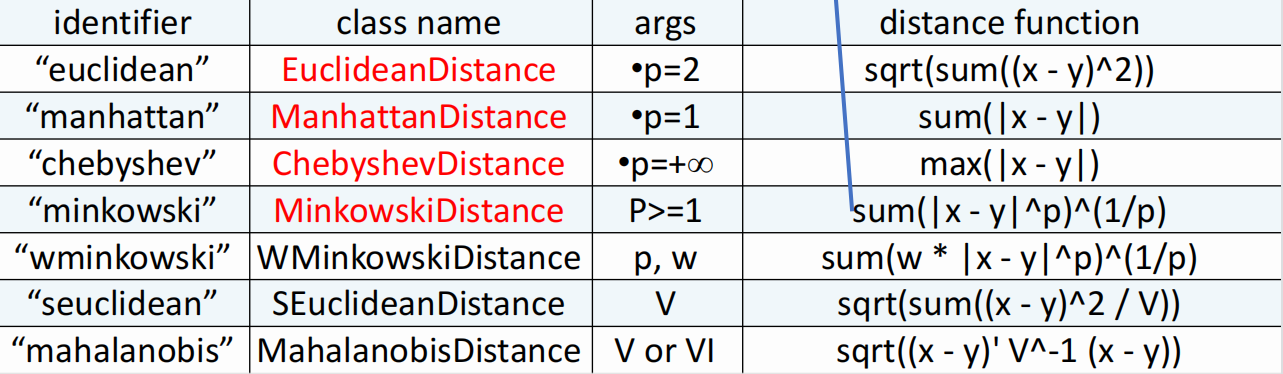
其中“minkowski”公式如下：

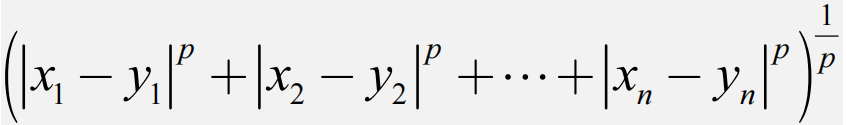
# 欧几里得距离（Euclidean Distance）：
from sklearn.metrics import pairwise_distances

X = [[0, 1], [1, 1]]
Y = [[1, 2], [2, 2]]
distances = pairwise_distances(X, Y, metric='euclidean')
print(distances)

# 曼哈顿距离（Manhattan Distance）：
distances = pairwise_distances(X, Y, metric='manhattan')
print(distances)

# 切比雪夫距离（Chebyshev Distance）：
distances = pairwise_distances(X, Y, metric='chebyshev')
print(distances)

# 余弦相似度（Cosine Similarity）：
distances = pairwise_distances(X, Y, metric='cosine')
print(distances)

二、最近邻算法的缺陷（1）

最近邻算法对噪声数据和异常值非常敏感。由于最近邻算法是基于距离度量的，因此如果样本数据中存在噪声数据或异常值，那么最近邻算法可能会将其误认为是有效数据，从而影响预测结果的准确性。

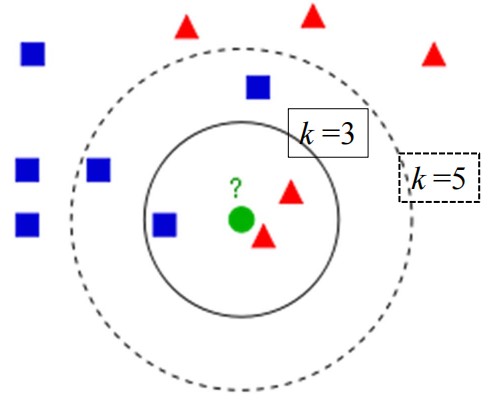
策略一：K近邻（k‐nearst neighbors, KNN）

1）计算测试数据与各个训练数据之间的距离；
2）按照距离的递增关系进行排序；
3）选取距离最小的k个点；
4）确定前k个点所在类别的出现频率；
5）返回前k个点中出现频率最高的类别作为测试数据的预测分类。

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 定义K近邻算法模型
knn = KNeighborsClassifier(n_neighbors=3,metric='minkowski',p=2)

# 训练模型
knn.fit(X_train, y_train)

# 进行预测
y_pred = knn.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

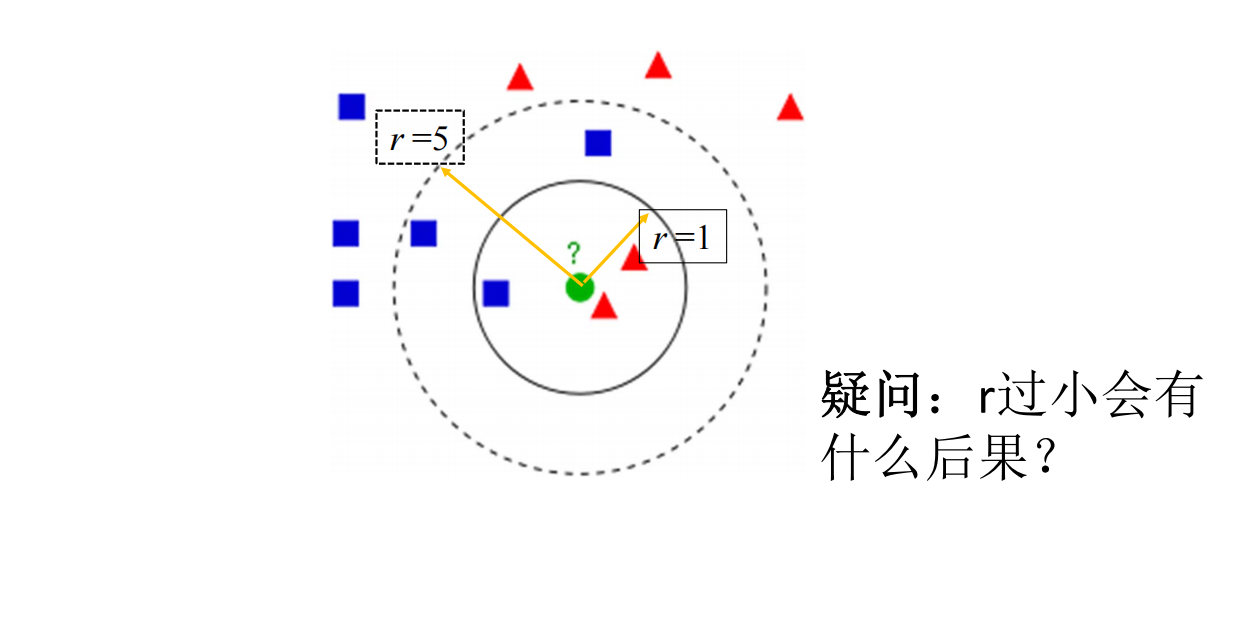
策略二：限定半径最近邻

from sklearn.datasets import load_iris
from sklearn.model_selection import train_test_split
from sklearn.neighbors import RadiusNeighborsClassifier
from sklearn.metrics import accuracy_score

# 加载数据集
iris = load_iris()
X = iris.data
y = iris.target

# 划分数据集
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3)

# 定义限定半径最近邻算法模型
rnn = RadiusNeighborsClassifier(radius=1,metric='minkowski',p=2)

# 训练模型
rnn.fit(X_train, y_train)

# 进行预测
y_pred = rnn.predict(X_test)

# 计算准确率
accuracy = accuracy_score(y_test, y_pred)
print("Accuracy:", accuracy)

半径值设置过小：如果半径值过小，那么可能无法找到足够数量的邻居样本。可以尝试增大半径值，以扩大邻居样本的范围。编译器报错you can try using larger radius, giving a label for outliers, or considering removing them from your dataset.

K（或r）的影响

选择较小的k值，就相当于用较小的领域中的训练实例进行预测，训练误差会减小，只有与输入实例较近或相似的训练实例才会对预测结果起作用，与此同时带来的问题是泛化误差会增大，换句话说，k值的减小就意味着整体模型变得复杂，容易发生过拟合；

选择较大的k值，就相当于用较大领域中的训练实例进行预测，其优点是可以减少泛化误差，但缺点是训练误差会增大。这时候，与输入实例较远（不相似的）训练实例也会对预测起作用，使预测发生错误，且k值的增大就意味着整体的模型变得简单。一个极端是k等于样本数m，则完全没有分类，此时无论输入实例是什么，都只是简单的预测它属于在训练实例中最多的类，模型过于简单。

最近邻算法的缺陷（2）

当样本不平衡时，即：一个类的样本容量很大，而其他类样本数量很小时，很有可能导致当输入一个未知样本时，该样本的k个邻居中大数量类的样本占多数。 但是这类样本并不接近目标样本，而数量小的这类样本很靠近目标样本。

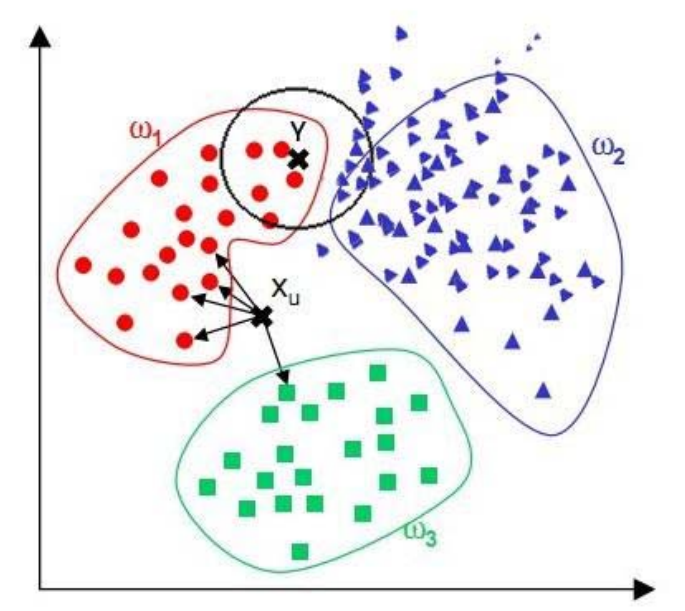
解决方案：加权

改进思路：和样本距离小的邻居权值大，和样本距离大的邻居权值则相对较小。

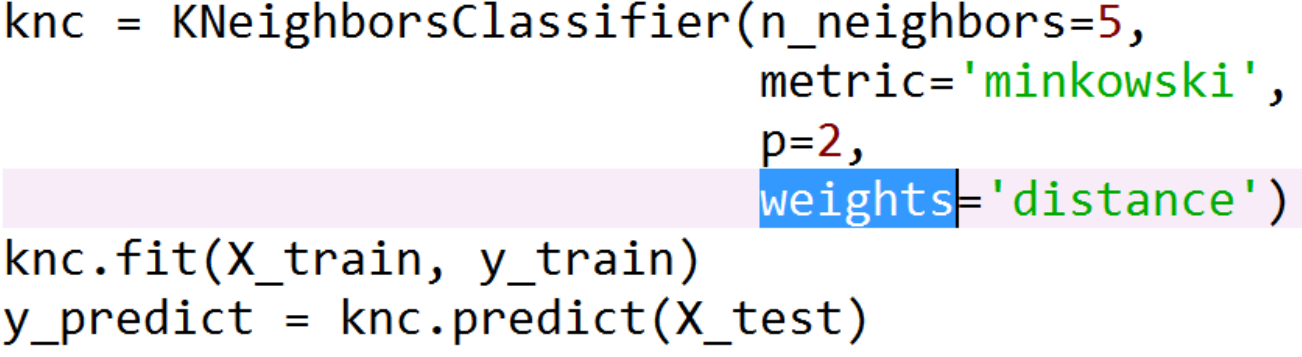
新问题：Brute force的计算量

knn暴力破解（Brute Force KNN）指的是一种基于遍历的最近邻搜索算法。在这个算法中，对于每个测试样本，都需要遍历整个训练数据集，计算其与每个训练样本之间的距离，并选择距离最近的k个训练样本作为其邻居样本。这种算法的时间复杂度为O(nd)，其中n是训练样本数量，d是特征维度。

k近邻法最简单的实现是线性扫描（穷举搜索），即要计算输入实例与每一个训练实例的距离。计算并存储好以后，再查找k近邻。当训练集
很大时，计算非常耗时。

解决方案：数据结构化之kd树和Ball树

KD树（K-Dimensional Tree）和Ball树（Ball Tree）都是用于最近邻搜索的数据结构，可以用于优化K近邻算法的效率。

KD树是一种二叉树结构，它根据数据集特征的分布情况，将数据集递归地划分为多个子空间，构建出一棵树结构。在最近邻搜索时，我们可以根据查询点的位置，递归地向下遍历树结构，找到离查询点最近的叶子节点，然后回溯到父节点，检查其它子节点是否有更近的邻居。由于KD树结构可以快速排除不必要的搜索区域，因此可以显著提高最近邻搜索的效率。

 knn = KNeighborsClassifier(n_neighbors=5, algorithm='kd_tree')

Ball树是一种树结构，它以数据集中的点为中心，通过球形区域来划分数据空间。Ball树结构递归地划分数据集，构建出一棵树结构。在最近邻搜索时，我们可以从根节点开始，递归地向下遍历树结构，找到包含查询点的最小球形区域，然后检查是否有更小的球形区域包含邻居点。Ball树结构可以快速排除不必要的搜索区域，因此也可以提高最近邻搜索的效率。

 knn = KNeighborsClassifier(n_neighbors=5, algorithm='ball_tree')

ball树 vs kd树 vs Brute force

•样本数量N和维度K.
•Brute force 查询时间以 O[KN]增长；
•Ball tree 查询时间大约以 O[Klog(N)]增长；
•KD tree 的查询时间与K的关系是很难精确描述。对于较小的K(小于20) ，
查询复杂度大约是O[log(N)] 。对于较大的K，复杂度接近O[KN]

作者：kobe在流浪
链接：https://www.zhihu.com/question/30957691/answer/338362344
来源：知乎
著作权归作者所有。商业转载请联系作者获得授权，非商业转载请注明出处

从数据量规模来看，当数据量小于5000时，虽然kd树和ball树搜索时间比暴力搜索时间复杂度低，但是计算机花费了更多的时间构建相关数据结构，当数据量较小的时候采用暴力搜索会比较节省时间，但是当数据量非常大的时候，采用kd树和ball树会更节省时间。

从数据维度来看，数据维度低的时候，kdtree和balltree时间复杂度相差不大，当数据维度高的时候，balltree的时间复杂度更低。
第一章：K近邻（分类）/练习/KNN速度比较.py

总结

优点

• 理论成熟，思想简单，既可以用来做分类也可以用来做回归；
• 可用于非线性分类；
• 和朴素贝叶斯之类的算法比，对数据没有假设，准确度高，对异常点不敏感；
• 由于KNN方法主要靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别的，对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合；
• 该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

缺点

• 计算量大，尤其是特征数非常多的时候；
• 样本不平衡的时候，对稀有类别的预测准确率低；（加权+限定半径）
• kd树、球树之类的模型建立需要大量的内存；
• 使用懒散学习方法，基本上不学习，导致预测时速度比起逻辑回归之类的算法慢。

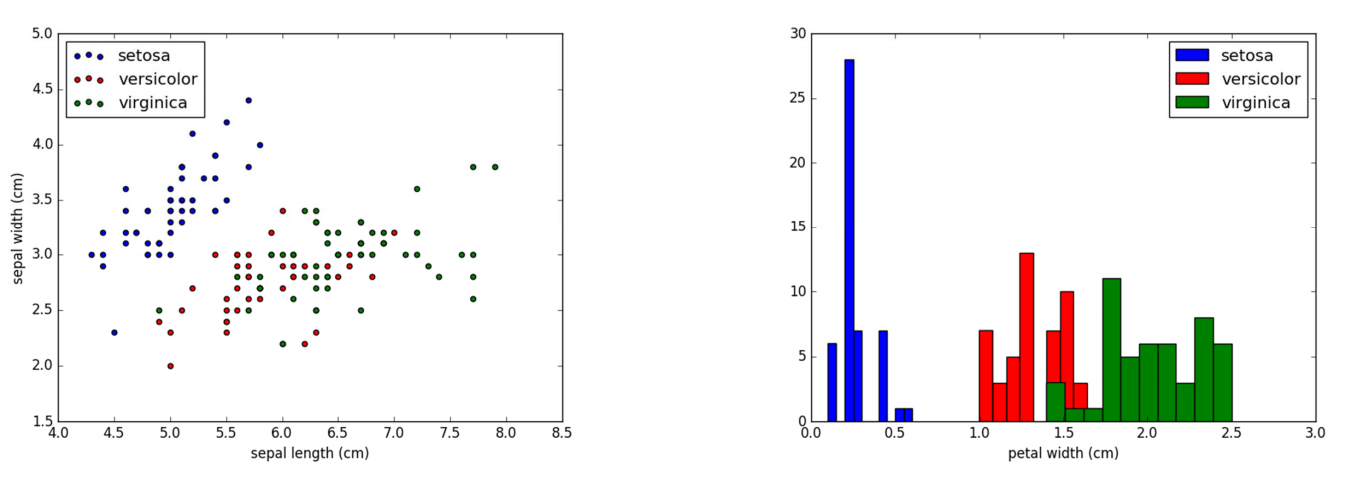
Iris数据简介

该数据集包含了4个属性：
Sepal.Length（花萼长度）， Sepal.Width（花萼宽度）
Petal.Length（花瓣长度）， Petal.Width（花瓣宽度）,单位是cm;

其中的一个种类与另外两个种类是线性可分离的，后两个种类是非线性可分离的。

参考资料

https://blog.csdn.net/pipisorry/article/details/53156836
https://www.cnblogs.com/21207‐iHome/p/6084670.html
tps://zhuanlan.zhihu.com/p/23083686
http://blog.sina.com.cn/s/blog_6f611c300101c5u2.html
http://scikit‐learn.org/stable/modules/generated/sklearn.neighbors.DistanceMetric.html
https://www.cnblogs.com/pinard/p/6065607.html