【测绘程序设计】C#伪距单点定位

文章目录

- 一、题目解读
- 二、界面设计
- 三、矩阵计算实现
- - 1、矩阵定义Matrix
  - 2、矩阵构造Matrix()
  - 3、单位矩阵MatrixE()
  - 4、加减乘操作符重载+-*
  - 5、矩阵转置transposs()
  - 6、矩阵求逆Inverse()
- 四、数据存储结构设计
- - 1、Sat类存一颗卫星的数据
  - 2、Epoch类存一个历元的数据
  - 3、DataCenter类存全部的数据
- 五、文件读取
- 六、最小二乘解算
- - 1、计算卫星到接收机近似点的距离R0
  - 2、构建设计矩阵B
  - 3、构建观测向量残差L
  - 4、构建权阵P
  - 5、计算协因数阵Q
  - 6、最小二乘计算增量dx
  - 7、估计位置pos
  - 8、计算验后残差V
  - 9、计算验后单位权中误差sigma0
  - 10、计算验后中误差sigma
  - 11、计算PDOP值
  - 12、循环解算过程
- 七、输出结果文件
- 八、代码汇总
- - 1、Sat.cs
  - 2、Epoch.cs
  - 3、DataCenter.cs
  - 4、Matrix.cs
  - 5、Algorithm.cs
  - 6、Form1.cs

一、题目解读

题目是简化了很多的GNSS伪距单点定位，而且比赛是单人四小时，可能到时候相比书上还要再简化一点。顺带一提，我的博客主要就是写GNSS，目前有RTKLIB、GraphGNSSLib、GNSS论文阅读，三个GNSS相关的专栏。

RTKLIB是最知名的GNSS定位算法开源程序；
GraphGNSSLib是一个因子图优化GNSS开源程序，基于ROS、Ceres非线性最小二乘库，用RTKLIB读取文件、然后重新用C++的方式组织数据、写算法。

伪距单点定位的基本原理就是用一台接收机同时接收4颗以上卫星，获取卫星到接收机之间的距离，根据空间后方交会的原理，构建伪距观测值和接收机位置间的方程组，解方程组得到接收机的位置。具体计算上还需要注意以下问题：

伪距观测值存在着很多的误差，有些可以建立模型修正（如：电离层延迟、对流层延迟、卫星钟差）、有些需要作为参数（如：接收机钟差）一并估计。伪距模型修正是在构建观测方程组之前，然后用修正后的伪距观测值计算观测残差。由于钟差作为参数，所以总的参数个数为4。
由于卫星数多于4颗，观测方程数大于参数个数，方程组超定，用最小二乘原理求出满足残差平方和最小的解。
由于观测方程不是线性的，得先线性化，在近似坐标处展开，求B、L矩阵。
由于各观测值的精度不同，引入权阵P来控制观测值对结果影响的权重，在本题中采用高度角定权模型。
解算完之后还要再求 $\sigma_0$ 、 $\sigma_{dx}$ 、 $\sigma_{dy}$ 、 $\sigma_{dz}$ ,PDOP，来衡量结果的精度。

书上给的C++代码里，这部分我觉得有问题，多了平方：

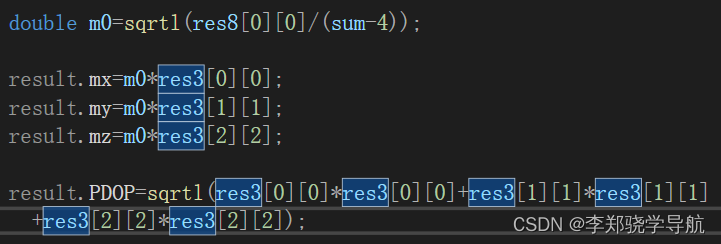
其中：res3是协因数阵 $Q$ ，由 $B^TPB)^{-1}$ 传播定律得来

代码里说 $Q$ 是协方差阵，这也有问题，协因数阵为协方差阵除以单位权方差。所以求 $\sigma_{dx}$ 、 $\sigma_{dy}$ 、 $\sigma_{dz}$ 是取协因数乘以单位权中误差。

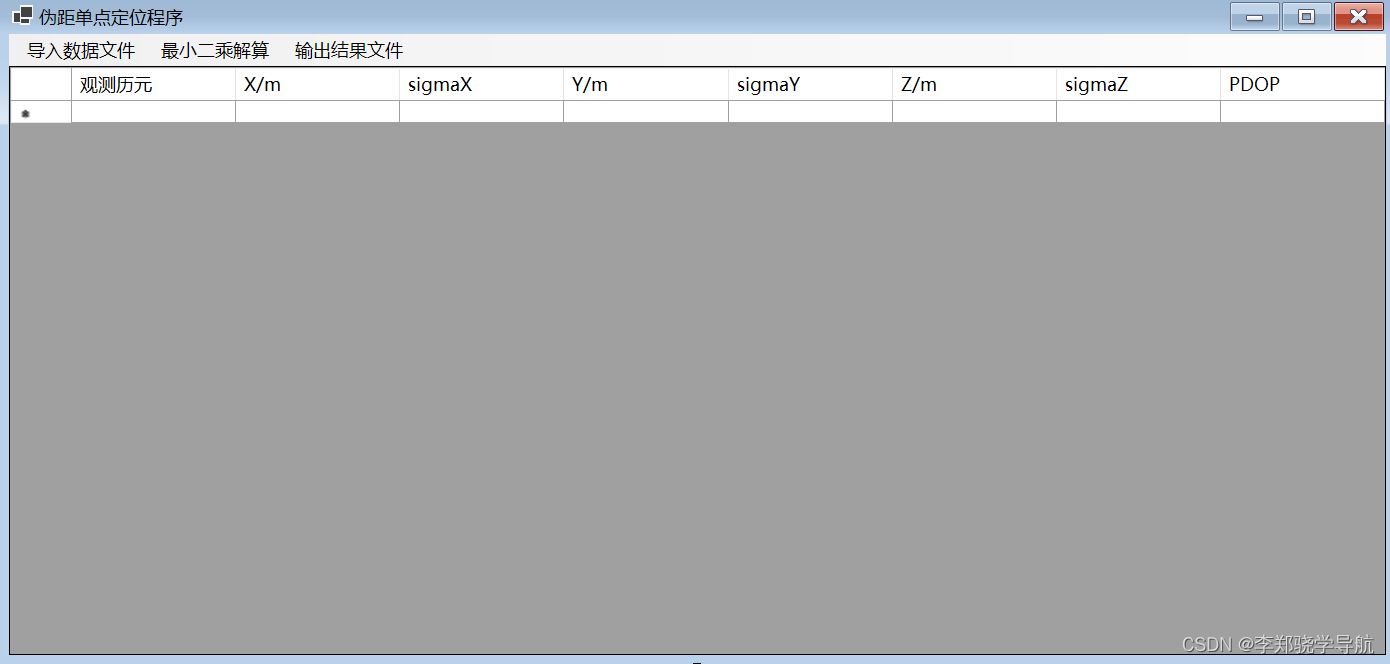
二、界面设计

做的比较简单，只用两个控件：一个menustrip，一个datagridview，达不到比赛的要求，还可以再加状态栏，加画图，加富文本框。

三、矩阵计算实现

1、矩阵定义Matrix

定义Matrix类来表示矩阵，矩阵的数据用二维double数组arr表示，字段m表示矩阵的行数、n表示矩阵的列数。

public class Matrix
{
    public int m;
    public int n;
    public double[,] arr;
    ........

m、n用于确定要开辟数组的大小，判断矩阵计算能否实现。
arr是矩阵数据存储的主体，操作数组元素：矩阵名.arr[行，列]

2、矩阵构造Matrix()

无参构造

public Matrix(){
    m = 0;
    n = 0;
    arr = new double[m, n];
}

拷贝构造：用另一个Matrix矩阵构造矩阵

public Matrix(Matrix s)
{
     this.m = s.m;
     this.n = s.n;
     arr = new double[m, n];
     this.arr = s.arr;
}

零矩阵构造：定义矩阵的行列数，元素全设为0

public Matrix(int mm, int nn)
{
     m = mm;
     n = nn;
     arr = new double[m, n];
}

3、单位矩阵MatrixE()

对角线元素全设置为1

public Matrix MatrixE(int mm, int nn)
{
     Matrix matrix = new Matrix(mm, nn);
     m = mm;
     n = nn;
     arr = new double[m, n];

     for (int i = 0; i < m; i++){
          for (int j = 0; j < n; j++){
              arr[i, j] = 1;
           }
     }
     return matrix;
}

4、加减乘操作符重载±*

加：需要行列数相等

static public Matrix operator +(Matrix A, Matrix B)
{
    Matrix C = new Matrix(A.m, A.n);
    //判断是否可以运算    
    if (A.m != B.m || A.n != B.n || A.m != C.m || A.n != C.n){
        System.Windows.Forms.MessageBox.Show("矩阵维数不同");
    }
    for (int i = 0; i < C.m; i++){
        for (int j = 0; j < C.n; j++){
            C.arr[i, j] = A.arr[i, j] + B.arr[i, j];
        }
    }

    return C;
}

减：同样，需要行列数相等

static public Matrix operator -(Matrix A, Matrix B)
{
    int i = 0;
    int j = 0;
    Matrix C = new Matrix(A.m, B.n);
    //判断是否可以运算    
    if (A.m != B.m || A.n != B.n ||
        A.m != C.m || A.n != C.n){
        Console.ReadKey();
    }
    for (i = 0; i < C.m; i++){
        for (j = 0; j < C.n; j++){
            C.arr[i, j] = A.arr[i, j] - B.arr[i, j];
        }
    }
    return C;
}

乘：前矩阵的列数等于后矩阵的行数，生成矩阵的维度为：前矩阵列数*后矩阵的行数

static public Matrix operator *(Matrix A, Matrix B)
{
    int i = 0;
    int j = 0;
    int k = 0;
    double temp = 0;
    Matrix C = new Matrix(A.m, B.n);
    //判断是否可以运算    
    if (A.m != C.m || B.n != C.n ||
        A.n != B.m){
        return C;
    }
    //运算    
    for (i = 0; i < C.m; i++){
        for (j = 0; j < C.n; j++){
            temp = 0;
            for (k = 0; k < A.n; k++){
                temp += A.arr[i, k] * B.arr[k, j];
            }
            C.arr[i, j] = temp;
        }
    }
    return C;
}

5、矩阵转置transposs()

public Matrix transposs(Matrix A)
{
    int i = 0;
    int j = 0;
    Matrix B = new Matrix(A.n, A.m);
    for (i = 0; i < B.m; i++){
        for (j = 0; j < B.n; j++){
            B.arr[i, j] = A.arr[j, i];
        }
    }
    return B;
}

6、矩阵求逆Inverse()

高斯-约旦法实现

public Matrix Inverse(Matrix matrix)
{
    matrix.arr = InverseMatrix(matrix.arr);
    return matrix;
}
        public double[,] InverseMatrix(double[,] matrix)
{
    int n = matrix.GetLength(0);
    double[,] result = new double[n, n];
    double[,] temp = new double[n, 2 * n];

    //将矩阵和单位矩阵拼接成一个2n*n的矩阵
    for (int i = 0; i < n; i++){
        for (int j = 0; j < n; j++){
            temp[i, j] = matrix[i, j];
            temp[i, j + n] = i == j ? 1 : 0;
        }
    }
    //高斯-约旦消元法
    for (int i = 0; i < n; i++){
        double tempValue = temp[i, i];
        for (int j = i; j < 2 * n; j++){
            temp[i, j] /= tempValue;
        }
        for (int j = 0; j < n; j++){
            if (j != i){
                tempValue = temp[j, i];
                for (int k = i; k < 2 * n; k++){
                    temp[j, k] -= tempValue * temp[i, k];
                }
            }
        }
    }
    //取出逆矩阵
    for (int i = 0; i < n; i++){
        for (int j = 0; j < n; j++){
            result[i, j] = temp[i, j + n];
        }
    }

    return result;
}

注意：

判断矩阵能否计算可以计算之后的处理可以写的更完善一点，我这基本上没处理，比赛项目的代码量小，如果项目大，最好写完善一点，矩阵计算出错了要能知道在哪一步出错；而且如果不是比赛可以直接用现成的线性代数库。
矩阵求逆用的高斯-约旦消元法，看起来代码量最小，好写但时间复杂度太大。正常计算都是用各种分解方法，再计算，性能好很多。
操作符重载实现加减乘，调用起来方便，一行公式不用拆成几条语句。
如果用C++，我可以重载括号运算符，实现矩阵元素的辅值和取值；C#我不熟，重载括号运算符可以实现取值，但由于C#没有指针，不知道能不能实现赋值，就没那么写。

四、数据存储结构设计

数据存储由Sat、Epoch、DataCenter三个层次实现：Sat卫星类存一个历元一颗卫星的数据，通过文件读取获取；Epoch类存一个历元的数据，包括一个历元内所有的Sat、最小二乘计算的中间矩阵、最终结果；DataCenter存全部的数据，包括所有的Epoch和近似坐标。在Form1类的开头需要先实例化DataCenter data = new DataCenter();，以便之后读写里面的数据，起到类似全局变量的作用。

1、Sat类存一颗卫星的数据

public class Sat
{
    public Matrix stapos;       //卫星位置
    public string PRN;          //卫星PRN
    public double satColck;     //卫星钟差
    public double elevation;    //卫星高度角
    public double cl;           //伪距
    public double tropDely;     //对流层延迟
    public double R0;           //估计几何距离
}

2、Epoch类存一个历元的数据

内含List<Sat> sats卫星列表

public class Epoch
{
    public int satNum;      //卫星数
    public int gpsTime;     //历元时间
    public List<Sat> sats;  //卫星观测值列表
    public Matrix dx;       //最小二乘求得的增量dx
    public Matrix pos;      //最小二乘估计的位置
    public double sigma0;   //延后单位权中误差
    public Matrix sigma;    //各个方向的中误差
    public double PDOP;     //PDOP
    public Matrix Q;        //协因数阵
    public Matrix P;        //权阵
    public Matrix B;        //设计矩阵
    public Matrix L;        //观测残差向量
    public Matrix V;        //后验残差
}

3、DataCenter类存全部的数据

内含List<Epoch> Epoches历元列表

public class DataCenter
{
    public List<Epoch> Epoches;     //历元列表
    public Matrix APPROX_POSITION;  //近似坐标
}

五、文件读取

private void 导入数据文件ToolStripMenuItem_Click(object sender, EventArgs e)
{
    try
    {
        OpenFileDialog opf = new OpenFileDialog();
        opf.Filter = "文本文件|*.txt";
        opf.Title = "请选择要导入的数据文件";
        if (opf.ShowDialog() == DialogResult.OK)
        {
            StreamReader sr = new StreamReader(opf.FileName);
            string[] lines = sr.ReadLine().Trim().Split(',', ':', '：', '(');
            data.APPROX_POSITION = new Matrix(3, 1, new double[3, 1] {
            {double.Parse( lines[1])},{ double.Parse( lines[2]) },{ double.Parse( lines[3])} });

            sr.ReadLine();  //第二行跳过

            //每一次while循环读取一个历元的数据
            Epoch epoch = new Epoch();
            Sat sat = new Sat();
            data.Epoches = new List<Epoch>();
            while (!sr.EndOfStream)
            {
                epoch = new Epoch();
                epoch.sats = new List<Sat>();

                lines = sr.ReadLine().Trim().Split(',', ':', '：');
                if (lines == null)
                {
                    break;
                }
                epoch.satNum = int.Parse(lines[1]);
                epoch.gpsTime = int.Parse(lines[3]);
                for (int i = 0; i < epoch.satNum; i++)
                {
                    sat = new Sat();
                    lines = sr.ReadLine().Trim().Split(',', ':', '：');
                    sat.PRN = lines[0];
                    sat.stapos = new Matrix(3, 1, new double[3, 1] {
                    {double.Parse( lines[1])},{ double.Parse( lines[2]) },
                    { double.Parse( lines[3])} });
                    sat.satColck = double.Parse(lines[4]);
                    sat.elevation = double.Parse(lines[5]);
                    sat.cl = double.Parse(lines[6]);
                    sat.tropDely = double.Parse(lines[7]);
                    epoch.sats.Add(sat);
                }
                data.Epoches.Add(epoch);
            }
        }
    }
    catch (Exception)
    {
        MessageBox.Show("文件读取出错，请检查文件是否正确！！");
        throw;
    }
    
}

执行流程：

写在一个大的try-catch里，以便异常捕获，正常开发应该写的跟细一点，但咱比赛就没这必要了。
创建文件对话框opf，ShowDialog()显示文件，获取文件全路径opf.FileName，创建读文件流sr。
读取第一行，获取近似坐标。
第二行跳过。
进入while(!sr.EndOfStream)循环，每次循环读取一个历元的数据到epoch：
- 先读取历元的开头，获取卫星数，历元时间到epoch。
- 根据卫星数for循环，一次读取一颗卫星的数据到sat里，再加到epoch的卫星列表里。
- 把epoch加到data的历元列表里。

注意：

原始数据文件的编码最好转成UTF-8再读取，否则一些中文的标点符号读取不出来，产生错误。转UTF-8方法：①代码内转换，需要知道文件的原始编码，写对应的转换代码。②手动转换：用Windows自带的记事本打开文件，点”另存为“，保存按钮坐标有编码格式，默认是文件的原始格式，选择“UTF-8”，以UTF-8保存。
标点符号要注意，给的乱的很，有中文全角、有英文乱角，split()的时候都选上吧。另外注意(也是需要加到split()里的。
用while (!sr.EndOfStream)做文件是否读完的判断，结尾可能有空行检验不到，如果不进行处理会产生异常，所以我还进行了非空判断if (lines == null) {break}。

六、最小二乘解算

1、计算卫星到接收机近似点的距离R0

$R_{0}^{j}=\sqrt{\left(X^{i}-X_{0}\right)^{2}+\left(Y^{i}-Y_{0}\right)^{2}+\left(Z^{i}-Z_{0}\right)^{2}}$

double R0 = Math.Sqrt(Math.Pow(epoch.sats[i].stapos.arr[0, 0] - pos0.arr[0, 0], 2) +
Math.Pow(epoch.sats[i].stapos.arr[1, 0] - pos0.arr[1, 0], 2)
+ Math.Pow(epoch.sats[i].stapos.arr[2, 0] - pos0.arr[2, 0], 2));

2、构建设计矩阵B

$\boldsymbol{B}=\left[\begin{array}{cccc} l^{1} & m^{1} & n^{1} & -1 \\ l^{2} & m^{2} & n^{2} & -1 \\ \vdots & \vdots & \vdots & -1 \\ l^{n} & m^{n} & n^{n} & -1 \end{array}\right]$

其中， $l^{i}=\frac{X^{i}-X_{0}}{R_{0}^{i}}$ ， $m^{\prime}=\frac{Y^{i}-Y_{0}}{R_{0}^{i}}$ ， $n^{i}=\frac{Z^{i}-Z_{0}}{R_{0}^{i}}$

epoch.B.arr[i, 0] = (epoch.sats[i].stapos.arr[0, 0] - pos0.arr[0, 0]) / R0;     
epoch.B.arr[i, 1] = (epoch.sats[i].stapos.arr[1, 0] - pos0.arr[1, 0]) / R0;
epoch.B.arr[i, 2] = (epoch.sats[i].stapos.arr[2, 0] - pos0.arr[2, 0]) / R0;
epoch.B.arr[i, 3] = -1;

3、构建观测向量残差L

$\boldsymbol{L}=\left[\begin{array}{c} P^{1} \\ P^{2} \\ \vdots \\ P^{n} \end{array}\right]-\left[\begin{array}{c} R_{0}^{1} \\ R_{0}^{2} \\ \vdots \\ R_{0}^{n} \end{array}\right]+\left[\begin{array}{c} d t^{1} \\ d t^{2} \\ \vdots \\ d t^{3} \end{array}\right]-\left[\begin{array}{c} d_{\text {trop }}^{1} \\ d_{\text {trop }}^{2} \\ \vdots \\ d_{\text {trop }}^{n} \end{array}\right]$

epoch.L.arr[i, 0] = epoch.sats[i].cl - R0 + epoch.sats[i].satColck - epoch.sats[i].tropDely;

注意正负号！！

4、构建权阵P

$\boldsymbol{P}_{j}=\left[\begin{array}{cccc} p_{1} & 0 & 0 & 0 \\ 0 & p_{2} & 0 & 0 \\ 0 & 0 & \cdots & 0 \\ 0 & 0 & 0 & p_{m} \end{array}\right]$

高度角定权，认为各卫星之间无相关性，只有对角线上有元素，其中 $p^{i}=\frac{1}{\sigma_{p^{i}}^{2}}=\frac{\sin \left(\theta^{i}\right)}{\sigma_{P, 0}^{2}}$ ， $\sigma_{P, 0}^{2}=0.04 \mathrm{~m}^{2}$

注意：计算正弦值需要将角度转为弧度

epoch.P.arr[i, i] = Math.Sin(epoch.sats[i].elevation * Math.PI / 180) / 0.04;

5、计算协因数阵Q

$\boldsymbol{Q}=\left(\boldsymbol{B}^{\mathrm{T}} P \boldsymbol{B}\right)^{-1}$

epoch.Q = pos0.Inverse((pos0.transposs(epoch.B) * epoch.P * epoch.B));

6、最小二乘计算增量dx

$x=-\left(B^{\top} P B\right)^{-1} B^{\top} P L=QB^{\top} P L$

Matrix zero = new Matrix(4, 1);
epoch.dx = zero - epoch.Q * pos0.transposs(epoch.B) * epoch.P * epoch.L;
Matrix _dx = new Matrix(3, 1);
_dx.arr[0, 0] = epoch.dx.arr[0, 0];
_dx.arr[1, 0] = epoch.dx.arr[1, 0];
_dx.arr[2, 0] = epoch.dx.arr[2, 0];

注意：不能直接在式子前面加负号-，只能用一个0向量来减去全式，实现取反。

7、估计位置pos

$\boldsymbol{X}=\boldsymbol{X}_{0}+\boldsymbol{d} \boldsymbol{x}=\left[\begin{array}{l} X_{0} \\ Y_{0} \\ Z_{0} \end{array}\right]+\left[\begin{array}{l} d X \\ d Y \\ d Z \end{array}\right]$

epoch.pos = pos0 + _dx;

8、计算验后残差V

$\cdot d x+L}$

epoch.V = epoch.B * epoch.dx + epoch.L;
Matrix vtpv = pos0.transposs(epoch.V) * epoch.P * epoch.V;

9、计算验后单位权中误差sigma0

$\sigma_{0}=\sqrt{\frac{\boldsymbol{V}^{\mathrm{T}} \boldsymbol{P} \boldsymbol{V}}{n-4}}$

epoch.sigma0 = Math.Sqrt(vtpv.arr[0, 0] / (epoch.satNum - 4));

10、计算验后中误差sigma

${\sigma_{d x}=\sigma_{0} \cdot \sqrt{q_{d x, d x}}, \sigma_{d Y}=\sigma_{0} \cdot \sqrt{q_{d x, d y}}, \sigma_{d z}=\sigma_{0} \cdot \sqrt{q_{d x, d x}}, \sigma_{d t}=\sigma_{0} \cdot \sqrt{q_{d t, d t}}}$

epoch.sigma = new Matrix(4, 1);
epoch.sigma.arr[0, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[0, 0]) ;
epoch.sigma.arr[1, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[1, 1]) ;
epoch.sigma.arr[2, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[2, 2]) ;
epoch.sigma.arr[3, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[3, 3]) ;

11、计算PDOP值

$\text { PDOP }=\sqrt{q_{d x, d x}+q_{d y, d y}+q_{d z, d z}}$

epoch.PDOP = Math.Sqrt(epoch.Q.arr[0, 0] + epoch.Q.arr[1, 1] + epoch.Q.arr[2, 2]);

12、循环解算过程

最小二乘的算法我分别写在了两个函数里，CalBLP()和Lsq()，计算的时候，就是简单的单历元平差，每个历元分别调用一遍两个函数：

for (int i = 0; i < data.Epoches.Count(); i++)
{
    algorithm.CalBLP(data.APPROX_POSITION, data.Epoches[i]);
    algorithm.Lsq(data.APPROX_POSITION, data.Epoches[i]);
}

注意：在我的计算过程中：

每个历元的近似值都用的是题目给的近似值，正常解算需要上一个历元的结果作为下一个历元的初值。
一个历元内只执行了一次最小二乘计算，正常解算需要一个历元内多次迭代，以弱化线性化和初值选取不准确的误差。
题目没有具体规定，写简单点就好。想实现迭代也不难，加个循环、每次计算完把结果赋值给近似坐标就行。

七、输出结果文件

private void 输出结果文件ToolStripMenuItem_Click(object sender, EventArgs e)
   {
       if (data.Epoches == null){
           MessageBox.Show("请先导入数据");
           return;
       }
       if (data.Epoches[0].B == null)
       {
           MessageBox.Show("请先进行最小二乘解算");
           return;
       }

       string Report = "";

       Report += "——————————————————————————————————————\n" +
           "———————————————— 最小二乘解算结果 ——————————————" +
           "\n——————————————————————————————————————\n" +
           "观测历元         X / m           σx / m           Y / m             σy / m          Z / m          σz / m    PDOP  \n";
      
       
       for (int i = 0; i < data.Epoches.Count; i++)
       {
           Report += data.Epoches[i].gpsTime.ToString() +"  :  "+
               data.Epoches[i].pos.arr[0, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[0, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[1, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[1, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[2, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[2, 0].ToString("0.0000") +"    "+
            data.Epoches[i].PDOP.ToString("0.0000") + "\n";
    }


    SaveFileDialog svf = new SaveFileDialog();
    svf.Filter = "文本文件|*.txt";
    if (svf.ShowDialog() == DialogResult.OK)
    {
        StreamWriter sw = new StreamWriter(svf.FileName);
        sw.Write(Report);
        sw.Flush();
    }

}

执行流程：

先进行判断，是否已经进行过文件读取，是否已经完成计算。
定义string类型变量Report，将文件的开头写到Report里，在循环将每一个历元的数据都加到Report里。
创建保存文件对话框svf，获取文件路径，创建文件IO流sw，将Report内容写入sw

八、代码汇总

1、Sat.cs

public class Sat
{
    public Matrix stapos;       //卫星位置
    public string PRN;          //卫星PRN
    public double satColck;     //卫星钟差
    public double elevation;    //卫星高度角
    public double cl;           //伪距
    public double tropDely;     //对流层延迟
    public double R0;           //估计几何距离
}

2、Epoch.cs

public class Epoch
{
    public int satNum;      //卫星数
    public int gpsTime;     //历元时间
    public List<Sat> sats;  //卫星观测值列表
    public Matrix dx;       //最小二乘求得的增量dx
    public Matrix pos;      //最小二乘估计的位置
    public double sigma0;   //延后单位权中误差
    public Matrix sigma;    //各个方向的中误差
    public double PDOP;     //PDOP
    public Matrix Q;        //协因数阵
    public Matrix P;        //权阵
    public Matrix B;        //设计矩阵
    public Matrix L;        //观测残差向量
    public Matrix V;        //延后残差
}

3、DataCenter.cs

public class DataCenter
{
    public List<Epoch> Epoches;     //历元列表
    public Matrix APPROX_POSITION;  //近似坐标
}

4、Matrix.cs

public class Matrix
{
    public int m;
    public int n;
    public double[,] arr;

    /// <summary>
    /// 创建一个矩阵0*0
    /// </summary>
    public Matrix(){
        m = 0;
        n = 0;
        arr = new double[m, n];
    }

    /// <summary>
    /// 拷贝构造
    /// </summary>
    /// <param name="s"></param>
    public Matrix(Matrix s)
    {
        this.m = s.m;
        this.n = s.n;
        arr = new double[m, n];
        this.arr = s.arr;
    }

    public Matrix(int mm, int nn, double[,] arr)
    {
        m = mm;
        n = nn;
        this.arr = arr;
    }

    public Matrix(int mm, int nn)
    {
        m = mm;
        n = nn;
        arr = new double[m, n];
    }

    /// <summary>
    /// 创建单位阵
    /// </summary>
    /// <param name="mm"></param>
    /// <param name="nn"></param>
    /// <returns></returns>
    public Matrix MatrixE(int mm, int nn)
    {
        Matrix matrix = new Matrix(mm, nn);
        m = mm;
        n = nn;
        arr = new double[m, n];

        for (int i = 0; i < m; i++){
            for (int j = 0; j < n; j++){
                arr[i, j] = 1;
            }
        }
        return matrix;
    }

    /// <summary>
    /// 重载操作符实现矩阵加法
    /// </summary>
    /// <param name="A"></param>
    /// <param name="B"></param>
    /// <returns></returns>
    static public Matrix operator +(Matrix A, Matrix B)
    {
        Matrix C = new Matrix(A.m, A.n);
        //判断是否可以运算    
        if (A.m != B.m || A.n != B.n || A.m != C.m || A.n != C.n){
            System.Windows.Forms.MessageBox.Show("矩阵维数不同");
        }
        for (int i = 0; i < C.m; i++){
            for (int j = 0; j < C.n; j++){
                C.arr[i, j] = A.arr[i, j] + B.arr[i, j];
            }
        }

        return C;
    }

    /// <summary>
    /// 重载操作符实现矩阵减法
    /// </summary>
    /// <param name="A"></param>
    /// <param name="B"></param>
    /// <returns></returns>
    static public Matrix operator -(Matrix A, Matrix B)
    {
        int i = 0;
        int j = 0;
        Matrix C = new Matrix(A.m, B.n);
        //判断是否可以运算    
        if (A.m != B.m || A.n != B.n ||
            A.m != C.m || A.n != C.n){
            Console.ReadKey();
        }
        for (i = 0; i < C.m; i++){
            for (j = 0; j < C.n; j++){
                C.arr[i, j] = A.arr[i, j] - B.arr[i, j];
            }
        }
        return C;
    }

    /// <summary>
    /// 重载操作符实现矩阵乘法
    /// </summary>
    /// <param name="A"></param>
    /// <param name="B"></param>
    /// <returns></returns>
    static public Matrix operator *(Matrix A, Matrix B)
    {
        int i = 0;
        int j = 0;
        int k = 0;
        double temp = 0;
        Matrix C = new Matrix(A.m, B.n);
        //判断是否可以运算    
        if (A.m != C.m || B.n != C.n ||
            A.n != B.m){
            return C;
        }
        //运算    
        for (i = 0; i < C.m; i++){
            for (j = 0; j < C.n; j++){
                temp = 0;
                for (k = 0; k < A.n; k++){
                    temp += A.arr[i, k] * B.arr[k, j];
                }
                C.arr[i, j] = temp;
            }
        }
        return C;
    }

    /// <summary>
    /// 矩阵转置
    /// </summary>
    /// <param name="A"></param>
    /// <returns></returns>
    public Matrix transposs(Matrix A)
    {
        int i = 0;
        int j = 0;
        Matrix B = new Matrix(A.n, A.m);
        for (i = 0; i < B.m; i++){
            for (j = 0; j < B.n; j++){
                B.arr[i, j] = A.arr[j, i];
            }
        }
        return B;
    }

    public double[,] InverseMatrix(double[,] matrix)
    {
        int n = matrix.GetLength(0);
        double[,] result = new double[n, n];
        double[,] temp = new double[n, 2 * n];

        //将矩阵和单位矩阵拼接成一个2n*n的矩阵
        for (int i = 0; i < n; i++){
            for (int j = 0; j < n; j++){
                temp[i, j] = matrix[i, j];
                temp[i, j + n] = i == j ? 1 : 0;
            }
        }
        //高斯-约旦消元法
        for (int i = 0; i < n; i++){
            double tempValue = temp[i, i];
            for (int j = i; j < 2 * n; j++){
                temp[i, j] /= tempValue;
            }
            for (int j = 0; j < n; j++){
                if (j != i){
                    tempValue = temp[j, i];
                    for (int k = i; k < 2 * n; k++){
                        temp[j, k] -= tempValue * temp[i, k];
                    }
                }
            }
        }
        //取出逆矩阵
        for (int i = 0; i < n; i++){
            for (int j = 0; j < n; j++){
                result[i, j] = temp[i, j + n];
            }
        }

        return result;
    }

    /// <summary>
    /// 矩阵求逆
    /// </summary>
    /// <param name="matrix"></param>
    /// <returns></returns>
    public Matrix Inverse(Matrix matrix)
    {
        matrix.arr = InverseMatrix(matrix.arr);
        return matrix;
    }


}

5、Algorithm.cs

public class Algorithm
{
    /// <summary>
    /// 计算BLP
    /// </summary>
    /// <param name="pos0"></param>
    /// <param name="epoch"></param>
    public void CalBLP(Matrix pos0, Epoch epoch)
    {
        epoch.B = new Matrix(epoch.satNum, 4);
        epoch.L = new Matrix(epoch.satNum, 1);
        epoch.P = new Matrix(epoch.satNum, epoch.satNum);
        for (int i = 0; i < epoch.satNum; i++)
        {
            //卫星到接收机近似点的距离R0
            double R0 = Math.Sqrt(Math.Pow(epoch.sats[i].stapos.arr[0, 0] - pos0.arr[0, 0], 2) +
               Math.Pow(epoch.sats[i].stapos.arr[1, 0] - pos0.arr[1, 0], 2)
               + Math.Pow(epoch.sats[i].stapos.arr[2, 0] - pos0.arr[2, 0], 2));

           //设计矩阵B
           epoch.B.arr[i, 0] = (epoch.sats[i].stapos.arr[0, 0] - pos0.arr[0, 0]) / R0;     
           epoch.B.arr[i, 1] = (epoch.sats[i].stapos.arr[1, 0] - pos0.arr[1, 0]) / R0;
           epoch.B.arr[i, 2] = (epoch.sats[i].stapos.arr[2, 0] - pos0.arr[2, 0]) / R0;
           epoch.B.arr[i, 3] = -1;

           //观测向量L
           epoch.L.arr[i, 0] = epoch.sats[i].cl - R0 + epoch.sats[i].satColck - epoch.sats[i].tropDely;

            //权阵P
            epoch.P.arr[i, i] = Math.Sin(epoch.sats[i].elevation * Math.PI / 180) / 0.04;
        }
    }


    /// <summary>
    /// 最小二乘解算
    /// </summary>
    /// <param name="pos0"></param>
    /// <param name="epoch"></param>
    public void Lsq(Matrix pos0, Epoch epoch)
    {
        Matrix zero = new Matrix(4, 1);

        //协因数Q
        epoch.Q = pos0.Inverse((pos0.transposs(epoch.B) * epoch.P * epoch.B));
        
        //增量dx
        epoch.dx = zero - epoch.Q * pos0.transposs(epoch.B) * epoch.P * epoch.L;
        Matrix _dx = new Matrix(3, 1);
        _dx.arr[0, 0] = epoch.dx.arr[0, 0];
        _dx.arr[1, 0] = epoch.dx.arr[1, 0];
        _dx.arr[2, 0] = epoch.dx.arr[2, 0];
        
        //估计位置
        epoch.pos = pos0 + _dx;

        //后验残差V
        epoch.V = epoch.B * epoch.dx + epoch.L;
        Matrix vtpv = pos0.transposs(epoch.V) * epoch.P * epoch.V;
        //单位权中误差
        epoch.sigma0 = Math.Sqrt(vtpv.arr[0, 0] / (epoch.satNum - 4));
        epoch.sigma = new Matrix(4, 1);
        epoch.sigma.arr[0, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[0, 0]) ;
        epoch.sigma.arr[1, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[1, 1]) ;
        epoch.sigma.arr[2, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[2, 2]) ;
        epoch.sigma.arr[3, 0] = epoch.sigma0 * Math.Sqrt(epoch.Q.arr[3, 3]) ;

        //PDOP值
        epoch.PDOP = Math.Sqrt(epoch.Q.arr[0, 0] + epoch.Q.arr[1, 1] + epoch.Q.arr[2, 2]);
    }
}

6、Form1.cs

public partial class Form1 : Form
{
    public Form1()
    {
        InitializeComponent();
    }

    DataCenter data = new DataCenter();

    private void dataGridView1_CellContentClick(object sender, DataGridViewCellEventArgs e)
    {

    }

    private void 导入数据文件ToolStripMenuItem_Click(object sender, EventArgs e)
    {
        try
        {
            OpenFileDialog opf = new OpenFileDialog();
            opf.Filter = "文本文件|*.txt";
            opf.Title = "请选择要导入的数据文件";
            if (opf.ShowDialog() == DialogResult.OK)
            {
                StreamReader sr = new StreamReader(opf.FileName);
                string[] lines = sr.ReadLine().Trim().Split(',', ':', '：', '(');
                data.APPROX_POSITION = new Matrix(3, 1, new double[3, 1] {
                {double.Parse( lines[1])},{ double.Parse( lines[2]) },{ double.Parse( lines[3])} });

                sr.ReadLine();  //第二行跳过

                //每一次while循环读取一个历元的数据
                Epoch epoch = new Epoch();
                Sat sat = new Sat();
                data.Epoches = new List<Epoch>();
                while (!sr.EndOfStream)
                {
                    epoch = new Epoch();
                    epoch.sats = new List<Sat>();

                    lines = sr.ReadLine().Trim().Split(',', ':', '：');
                    if (lines == null)
                    {
                        break;
                    }
                    epoch.satNum = int.Parse(lines[1]);
                    epoch.gpsTime = int.Parse(lines[3]);
                    for (int i = 0; i < epoch.satNum; i++)
                    {
                        sat = new Sat();
                        lines = sr.ReadLine().Trim().Split(',', ':', '：');
                        sat.PRN = lines[0];
                        sat.stapos = new Matrix(3, 1, new double[3, 1] {
                        {double.Parse( lines[1])},{ double.Parse( lines[2]) },
                        { double.Parse( lines[3])} });
                        sat.satColck = double.Parse(lines[4]);
                        sat.elevation = double.Parse(lines[5]);
                        sat.cl = double.Parse(lines[6]);
                        sat.tropDely = double.Parse(lines[7]);
                        epoch.sats.Add(sat);
                    }
                    data.Epoches.Add(epoch);
                }
            }
        }
        catch (Exception)
        {
            MessageBox.Show("文件读取出错，请检查文件是否正确！！");
            throw;
        }
        
    }

    private void 最小二乘解算ToolStripMenuItem_Click(object sender, EventArgs e)
    {
        if (data.Epoches==null)
        {
            MessageBox.Show("请先导入数据");
            return;
        }

        Algorithm algorithm = new Algorithm();

        //遍历每一个历元，最小二乘解算
        for (int i = 0; i < data.Epoches.Count(); i++)
        {
            algorithm.CalBLP(data.APPROX_POSITION, data.Epoches[i]);
            algorithm.Lsq(data.APPROX_POSITION, data.Epoches[i]);
        }

        //将解算结果输出到表格
        dataGridView1.RowCount = data.Epoches.Count;
        for (int i = 0; i < data.Epoches.Count; i++)
        {
            dataGridView1.Rows[i].Cells[0].Value = data.Epoches[i].gpsTime;
            dataGridView1.Rows[i].Cells[1].Value = data.Epoches[i].pos.arr[0, 0];
            dataGridView1.Rows[i].Cells[2].Value = data.Epoches[i].sigma.arr[0, 0];
            dataGridView1.Rows[i].Cells[3].Value = data.Epoches[i].pos.arr[1, 0];
            dataGridView1.Rows[i].Cells[4].Value = data.Epoches[i].sigma.arr[1, 0];
            dataGridView1.Rows[i].Cells[5].Value = data.Epoches[i].pos.arr[2, 0];
            dataGridView1.Rows[i].Cells[6].Value = data.Epoches[i].sigma.arr[2, 0];
            dataGridView1.Rows[i].Cells[7].Value = data.Epoches[i].PDOP;
        }

    }

    private void 输出结果文件ToolStripMenuItem_Click(object sender, EventArgs e)
    {
        if (data.Epoches == null){
            MessageBox.Show("请先导入数据");
            return;
        }
        if (data.Epoches[0].B == null)
        {
            MessageBox.Show("请先进行最小二乘解算");
            return;
        }

        string Report = "";

        Report += "——————————————————————————————————————\n" +
            "———————————————— 最小二乘解算结果 ——————————————" +
            "\n——————————————————————————————————————\n" +
            "观测历元         X / m           σx / m           Y / m             σy / m          Z / m          σz / m    PDOP  \n";
       
        
        for (int i = 0; i < data.Epoches.Count; i++)
        {
            Report += data.Epoches[i].gpsTime.ToString() +"  :  "+
                data.Epoches[i].pos.arr[0, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[0, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[1, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[1, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[2, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[2, 0].ToString("0.0000") +"    "+
                data.Epoches[i].PDOP.ToString("0.0000") + "\n";
        }


        SaveFileDialog svf = new SaveFileDialog();
        svf.Filter = "文本文件|*.txt";
        if (svf.ShowDialog() == DialogResult.OK)
        {
            StreamWriter sw = new StreamWriter(svf.FileName);
            sw.Write(Report);
            sw.Flush();
        }

    }
}
  "\n——————————————————————————————————————\n" +
            "观测历元         X / m           σx / m           Y / m             σy / m          Z / m          σz / m    PDOP  \n";
       
        
        for (int i = 0; i < data.Epoches.Count; i++)
        {
            Report += data.Epoches[i].gpsTime.ToString() +"  :  "+
                data.Epoches[i].pos.arr[0, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[0, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[1, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[1, 0].ToString("0.0000") +"    "+
                    data.Epoches[i].pos.arr[2, 0].ToString("0.0000") +"    "+ data.Epoches[i].sigma.arr[2, 0].ToString("0.0000") +"    "+
                data.Epoches[i].PDOP.ToString("0.0000") + "\n";
        }


        SaveFileDialog svf = new SaveFileDialog();
        svf.Filter = "文本文件|*.txt";
        if (svf.ShowDialog() == DialogResult.OK)
        {
            StreamWriter sw = new StreamWriter(svf.FileName);
            sw.Write(Report);
            sw.Flush();
        }

    }
}