C++算法：排序

排序之一（插入、冒泡、快速排序）

文章目录

C++算法：排序
前言
一、十大排序法性能
二、各算法实现
- 1、插入排序
- 2、冒泡排序
- 3、快速排序
原创文章，未经许可，严禁转载

前言

排序算法很多，一直有十大经典的说法。实际工作中除了个别有争议的排序算法，各有各擅长的领域，不能因为选择排序又慢又简单就小看它，有时候还真是非它不可。也不能因为桶排序、计数排序是理论上时间复杂度最小的就觉得能包圆所有排序工作。

一、十大排序法性能

这里用一张表格来说明各种排序算法的性能比较：

算法名称	最好时间复杂度	平均时间复杂度	最坏时间复杂度	空间复杂度	稳定性
插入排序	O(n)	O(n²)	O(n²)	O(1)	是
冒泡排序	O(n)	O(n²)	O(n²)	O(1)	是
快速排序	O(NlogN)	O(NlogN)	O(n²)	O(logN)	否
归并排序	O(NlogN)	O(NlogN)	O(NlogN)	O(n)	是
希尔排序	O(NlogN)	O(NlogN)	O(NlogN)	O(1)	否
选择排序	O(n²)	O(n²)	O(n²)	O(1)	否
堆排序	O(NlogN)	O(NlogN)	O(NlogN)	O(1)	否
-------------	------------------------	----------------------	----------------------	-----------------	---------
计数排序	O(n)	O(n)	O(n)	O(n)	是
桶排序	O(n)	O(n)	O(n)	O(n)	是
基数排序	O(n*K)	O(n*K)	O(n*K)	O(n)	是

以上隔开的前七个算法是比较排序，后三个是非比较排序。

比较排序是通过比较元素之间的次序来确定它们在最终结果中的位置，简单说就是比大小了。
非比较排序则是通过确定每个元素之前应该有多少个元素来进行排序的。
比较排序的优点是适用于各种规模的数据，也不在乎数据的分布，都能进行排序。可以说，比较排序适用于一切需要排序的情况。
非比较排序时间复杂度低，但由于非比较排序需要占用空间来确定唯一位置，所以对数据规模和数据分布有一定的要求。

二、各算法实现

以下动图来源本站此文，顺便说一下，这篇文章写得很好。我都想直接转的，可惜是JAVA实现，与笔者主题不符。就借动图来一用，具体动图来源不可考。反正我是从此文借来，如有侵权、请留言指正。

1、插入排序

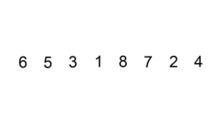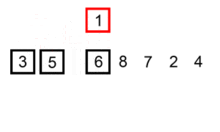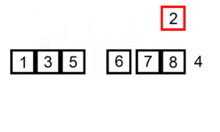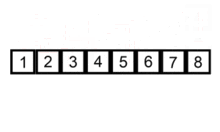
在这里插入图片描述
插入排序在对小规模数据进行排序时很常用。它有点类似于我们斗地主抓牌的过程，第一张扑克牌拿到手后，之后每抓到一张都按大小放置，抓完了牌就自然是有序的。

代码如下（示例）：

#include <iostream>
#include <vector>

using namespace std;

void insert_sort(vector<int> &vec){
    int n = vec.size();
    int curr;                          //当前要排的
    for (int i=1; i<n; i++){
        curr = vec[i];         
        int j = i - 1;                //另一个下标指针，指向被比较的
        while (j>=0 && curr<vec[j]){
            vec[j+1] = vec[j];        //符合条件，就将当前替换为前一个，因为当前已备份到curr
            j--;                      //一直向前比较
        }
        vec[j+1] = curr;             //将当前放入合适的位置，j经过循环会停在第一个小于curr的元素上
    }    
}

int main(){
    vector<int> vec = {6, 5, 3, 1, 8, 7, 2, 4};
    insert_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

代码使用了图中同样的数据，使用了STL中的vector，对链表也是可行的，不过要用迭代器，不能直接用[]运算。通过遍历数组中的每个元素，将当前元素与前面的元素进行比较并交换位置，直到当前元素大于前面的元素为止。这样可以保证在当前元素之前的所有元素都是有序的。最终，整个数组都将变为有序。

2、冒泡排序

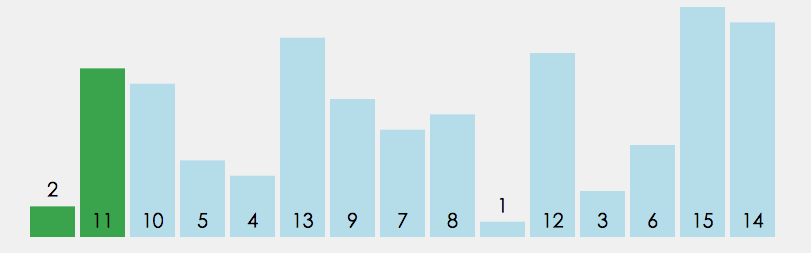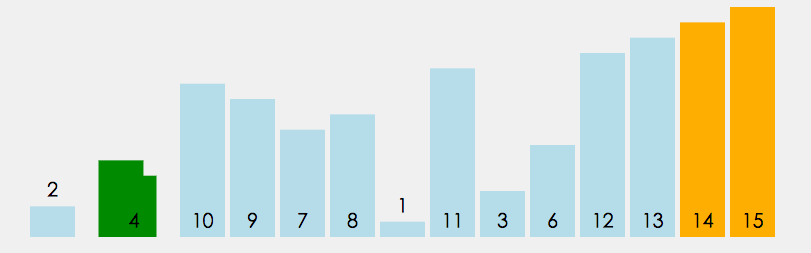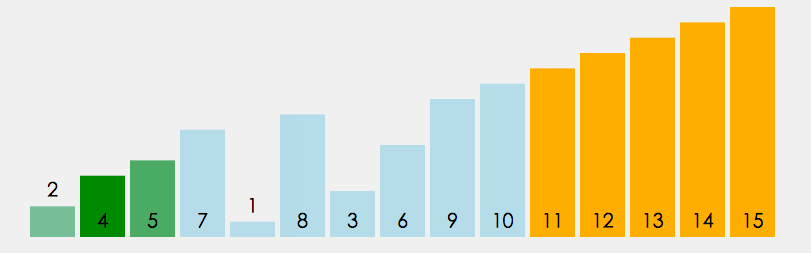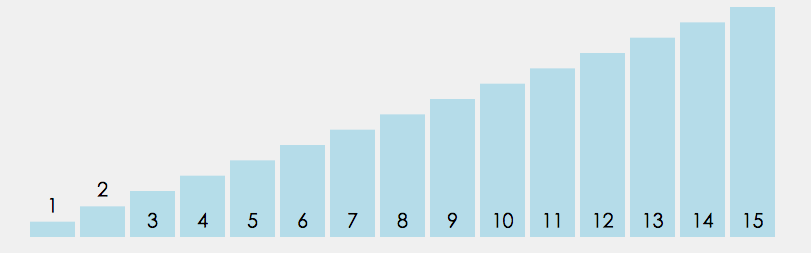
在这里插入图片描述
冒泡排序（也叫气泡排序（bubble sort），名字来源于水中的大气泡总是在小气泡之上）很好理解，前一个与后一个比较大小，小的放前，大的放后。如此一个个比过去，多来几遍自然就排序完成了。当某一次排序没有产生交换操作，那就可以认定排序完成。这个排序算法和插入排序一样，比较适合小规模的数据，并且在数据基本有序的时候是非常好用的，实现简单，效率很高。

代码如下（示例）：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;

void bubble_sort(vector<int> &vec){
    int n = vec.size();
    int i = 0, flag;                    //i 是循环计数，flag用于表示有没有交换动作
    do{
        flag = 0;                       //先认为没有交换
        for (int j=0; j<n-i-1; j++){
            if (vec[j] > vec[j+1]){
                swap(vec[j], vec[j+1]);    //交换大小元素
                flag = 1;                 //产生了交换动作
            } 
        }    
    } while (++i < n && flag);            //没有交换动作或循环次数能保证有序就停止了
}

int main(){
    vector<int> vec = {2, 11, 10, 5, 4, 13, 9, 7, 8, 1, 12, 3, 6, 15, 14};
    bubble_sort(vec);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}

上面的代码中引入了algorithm中的swap函数来实现元素交换。当然也可以自己写一个，这个很容易。实现过程看注释也就明白了，特别的，在排序函数最后的while条件中，++i < n 可以改成++i < n-1，当然实际情况是很少真需要 n-1 次的，因为flag这个条件会在排序成功后停止循环。只有最小值是最后一个元素的情况才会循环 n-1 次（因为最小值元素需要n-1次才能跑到最前面）。

另外冒泡排序有个很有名的改良版本，叫鸡尾酒排序（也叫双向冒泡排序），看名字也就知道怎么改良了，事实上它和冒泡排序的时间、空间复杂度是一样的，更适合于基本有序的情况而已。

3、快速排序

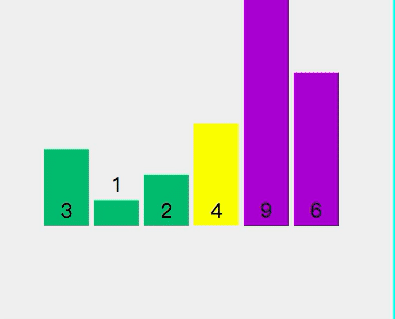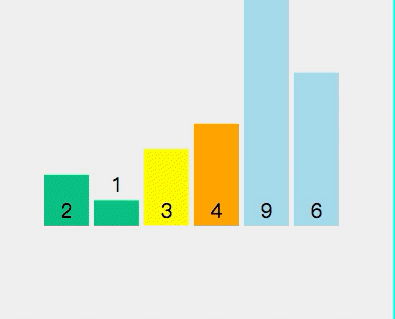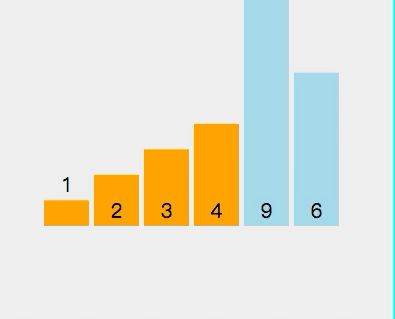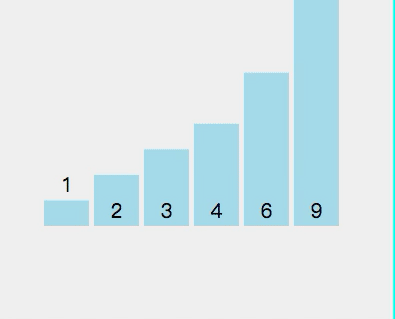
在这里插入图片描述
前面两种排序算法都只适合小规模数据，且平均时间复杂度很高，通常适用于特定情况。而快速排序是一种高效的排序算法，它采用了分治的思想，适用于较大规模数据的情况。这个排序法在实践中使用得很多，也是实践证明最有效的排序法，很多IT大厂面试时往往会要求写一个快速排序算法，本文也重点写了这个算法。其基本步骤如下：

从数列中挑出一个元素作为基准元素，也称之为划界元素。
将所有比基准元素小的元素放到基准元素的左边，所有比基准元素大的元素放到基准元素的右边。
对基准元素左右两边的子序列递归执行第1步和第2步，直到序列中所有元素都有序。

快速排序的平均时间复杂度为O(NlogN)，最坏情况下的时间复杂度为O(n^2)，但这种情况并不常见。快速排序通常明显比其他O(NlogN)算法更快，因为它的内部循环可以在大部分架构上非常高效地实现。既然采用了递归算法，那就有可能产生递归深度太深的情况，如果数据规模太大也是不适用的。对于C++标准库内置的sort来说，在这种情况下会转用堆排序。

代码如下（示例）：

#include <iostream>
#include <vector>
#include <algorithm>

using namespace std;
//以最后元素划界的写法
void quick_sort_b(vector<int> &vec, int left, int right) {
    if (left < right) {                          
        int base = vec[right];                     //以最后元素划界
        int i = left - 1;                          //前元素下标指针
        for (int j = left; j <= right - 1; j++){   // j 为后元素下标指针
            if (vec[j] <= base) {                 
                i++;                               
                swap(vec[i], vec[j]);         //循环交换，实际效果是小于划界的都到前面去了
            }
        }
        swap(vec[i + 1], vec[right]);      //把划界元素放到中间，当前i是小于划界的，i+1是大的
        int pi = i + 1;                    //递归是要排除划界的
        quick_sort_b(vec, left, pi - 1);
        quick_sort_b(vec, pi + 1, right);
    }
}

//以最左元素划界的写法
void quick_sort_f(vector<int> &vec, int left, int right) {
    if (left < right) {
        int base = vec[left];                    //以最左元素划界
        int i = left;                            //前元素下标指针
        for (int j = left+1; j <= right; j++){   // j 为后元素下标指针
            if (vec[j] <= base) {
                i++;
                swap(vec[i], vec[j]);        //循环交换，实际效果是小于划界的都到前面去了
            }
        }
        swap(vec[i], vec[left]);          //把划界元素放到中间，当前i是小于划界的
        int pi = i + 1;                   //递归前排除划界元素
        quick_sort_f(vec, left, pi-1);
        quick_sort_f(vec, pi+1, right);
    }
}

int main(){
    vector<int> vec = {3, 1, 2, 4, 9, 6};
    //quick_sort_b(vec, 0, vec.size()-1);
    quick_sort_f(vec, 0, vec.size()-1);
    for (auto it=vec.begin(); it!=vec.end(); it++){
        cout << *it << " ";
    }
    return 0;
}