只能说回溯实在是诡异，刚看到这题目思路一点不清晰，想着用回溯想到一点写一点，就这样诡异的出来了。

主要回溯思想，由于冰淇淋基料只能选一种，那就对数组遍历，每次对一种冰淇淋基料继续回溯，用res保存最好的情况，每种配料可以选择最多两份，这里使用many来标注当前配料是否还能选择，能选就选两份回溯，不能就去下一份回溯，当成本大于目标时，就不用再选了，越选差只会越大，维护最小差值，差值相等时取成本低的一份

 

class Solution {
    int res=Integer.MAX_VALUE;//保存最佳的成本
    public int closestCost(int[] baseCosts, int[] toppingCosts, int target) {
        for(int base:baseCosts){
            backtracking(toppingCosts,target,0,base,0);
            if(res==target) return res;//能达到目标就不用再计算了
        }
        return res;
    }
    public void backtracking(int[] toppingCosts,int target,int index,int sum,int many){
        int dif1=Math.abs(sum-target);//当前组合和目标的差
        int dif2=Math.abs(res-target);//保存最佳组合
        if(dif1<dif2){
            res=sum;
        }
        if(dif1==dif2&&sum<res){//差值一样取小值
            res=sum;
        }
        if(sum>=target){//成本以及高于目标，没必要再拿了
            return;
        }
        for(int i=index;i<toppingCosts.length;i++){
            if(many==0){//当前配料能取两份，取当前两份试试
                backtracking(toppingCosts,target,i,sum+toppingCosts[i],many+1);
            }
            backtracking(toppingCosts,target,i+1,sum+toppingCosts[i],0);//去下一份
        }

    }
}

---

 

 双指针判断回文串，没啥营养，不过我的水平只能写写这种题。

class Solution {
    public String firstPalindrome(String[] words) {
        for(String str:words){
            if(isBack(str)){
                return str;
            }
        }
        return "";
    }
    public boolean isBack(String str){
        int i=0;
        int j=str.length()-1;
        while(i<j){
            if(str.charAt(i)!=str.charAt(j))
            return false;
            i++;
            j--;
        }
        return true;
    }
}

---

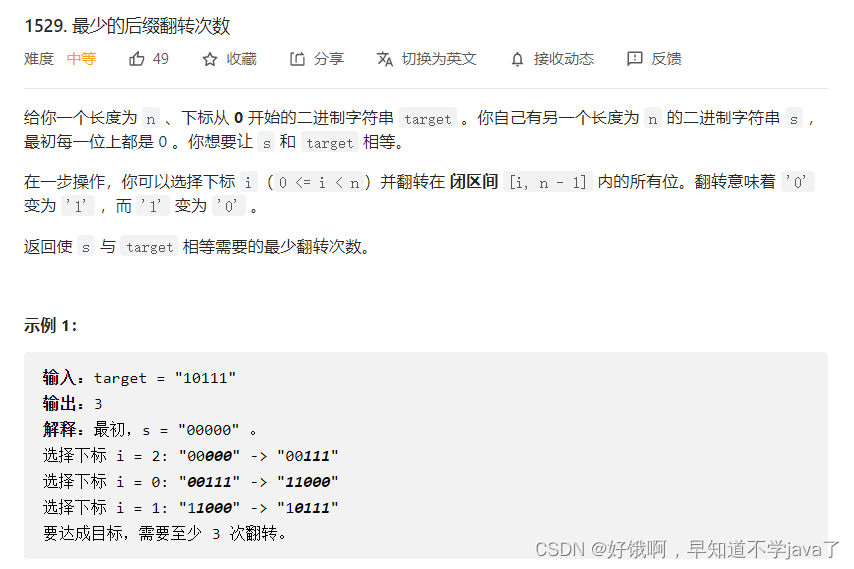
 好消息，这个题目和我以前写过的一个牛转向的问题很像，坏消息，我忘得一干二净，再好消息，找规律硬找出来了，发现和那个牛转向问题应该不一样，因为那个我不会。

遇事不决找规律，多试几个例子

101：000->001->010->101;

很容易就能发现1001等同于101的 11011也等同于101这种；不理解可以反转试试

那么 10101:00000->00001->00010->00101->01010->10101

从00101想把隔了0前面的1变化，需要两次，和101的001想把前面的0变成1同理，

0和1连续重复出现的都是等同的，比如1100110011等同上面的 那么再看末尾是0的情况 100:000->011->100

重复一样等同 就可以知道，末尾连续1反转次数加1，再隔连续个0遇见连续的1反转次数加2...

 

class Solution {
    public int minFlips(String target) {
        int n=target.length()-1;
        int res=0;//保存结果
        if(target.charAt(n)=='1')
        res++;
        for(n=n-1;n>=0;n--){//从倒数第二个开始逆序遍历
            if(target.charAt(n)=='1'&&target.charAt(n+1)=='0')//遇到新的连续1就需要多反转两次
            res+=2;
        }
        return res;
    }
}