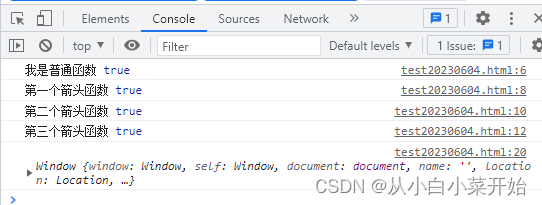
import numpy as np
import matplotlib.pyplot as plt
#matplotlib inline
from matplotlib import image
from matplotlib import pyplot as plt
import cv2
# 解析文件,按空格分割字段,得到一个浮点数字类型的矩阵
def loadDataSet(fileName):
dataMat = [] # 初始化一个空列表,文件的最后一个字段是类别标签
fr = open(fileName) # 读取文件
for line in fr.readlines(): # 循环遍历文件所有行
curLine = line.strip().split(' ') # 切割每一行的数据
fltLine = list(map(float, curLine)) # 映射所有的元素为 float(浮点数)类型
dataMat.append(fltLine) # 将数据追加到dataMat
return dataMat # 返回dataMat
# 计算欧几里得距离
def distEclud(vecA, vecB):
return sqrt(sum(power(vecA - vecB, 2))) # 求两个向量之间的距离
# 构建聚簇中心,取k个(此例中为4)随机质心
def randCent(dataSet, k):
n = shape(dataSet)[1] #获取特征值数量:3列
centroids = mat(zeros((k,n))) #初始化质心为0,创建(k,n)个以零填充的矩阵k=4行,3列
for j in range(n): #循环遍历特征值
#下面计算的分别是横坐标、纵坐标与类别标签
minJ = min(dataSet[:,j]) #计算每一列的最小值
maxJ = max(dataSet[:,j]) #计算每一列的最大值
rangeJ = float(maxJ - minJ) #计算每一列的范围值
centroids[:,j] = minJ + rangeJ * random.rand(k, 1) #计算每一列的质心,并将值赋给centroids
return centroids #返回质心
def kMeans(dataSet, k, distMeans =distEclud, createCent = randCent):
m = shape(dataSet)[0]#查看数据集行数100
print(m)
# clusterAssment包含两个列:一列记录簇索引值,第二列存储误差(误差是指当前点到簇质心的距离,后面会使用该误差来评价聚类的效果)
clusterAssment = mat(zeros((m,2)))
#centroids = randCent(dataSet, k) # 创建质心,随机K=4个质心
centroids = np.mat(loadDataSet('./after_label_training_center.txt')) # 创建质心,随机K=4个质心
clusterChanged = True # 用来判断聚类是否已经收敛,启动初始循环
while clusterChanged:
clusterChanged = False;#只有全部的点都被分配完毕后才停止
# 遍历所有数据找到距离每个点最近的质心,
# 可以通过对每个点遍历所有质心并计算点到每个质心的距离来完成
for i in range(m):#一共m行数据
minDist = inf;#无穷
minIndex = 1;#任意值
for j in range(k):#第j个质心
# 计算数据点到质心的距离
# 计算距离是使用distMeans函数给出的距离公式,默认距离函数是distEclud欧几里得距离
distJI = distMeans(centroids[j,:], dataSet[i,:])#第i个数据点与第j个质心比较
#如果距离比minDist(最小距离)还小,更新minDist(最小距离)和最小质心的index(索引)
#这里第一个肯定是要更新的,因为任何值都比无穷大,要小
if distJI < minDist:
minDist = distJI; minIndex = j # 如果第i个数据点到第j个中心点更近,则将i归属为j簇
# 如果任一点的簇分配结果发生改变,则更新clusterChanged为true.
if clusterAssment[i,0] != minIndex:
clusterChanged = True;
clusterAssment[i,:] = minIndex,minDist**2 # 更新簇分配结果为最小质心的index(索引),minDist(最小距离)的平方(误差)
for cent in range(k): # 重新计算中心点,遍历所有质心并更新它们的取值
ptsInClust = dataSet[nonzero(clusterAssment[:,0].A == cent)[0]] # 通过数据过滤来获得给定簇的所有点
centroids[cent,:] = mean(ptsInClust, axis = 0) # 计算所有点的均值,axis=0表示沿矩阵的列方向进行均值计算
return centroids, clusterAssment #返回所有的类质心与点分配结果
def showCluster(dataSet,k,centroids,clusterAssment):
m,n = dataSet.shape
if n != 2:
print("数据不是二维的")
return 1
#二维数据标准
mark = ['or', 'ob', 'og', 'ok', '^r', '+r', 'sr', 'dr', '<r', 'pr']
if k > len(mark):
print("k值太大了")
return 1
#分类不太多
# 绘制所有的样本
for i in range(m):
markIndex = int(clusterAssment[i,0])
plt.plot(dataSet[i,0],dataSet[i,1],mark[markIndex])#数据点形状颜色
mark = ['Dr', 'Db', 'Dg', 'Dk', '^b', '+b', 'sb', 'db', '<b', 'pb']#质心与形状颜色
# 绘制质心
for i in range(k):
plt.plot(centroids[i,0],centroids[i,1],mark[i],markersize=13)
plt.show()
#datMat1 = np.mat(loadDataSet('./data_epi_no_label.txt'))
datMat1 = np.mat(loadDataSet('./nolabel_expand.txt'))
datMat = np.mat(loadDataSet('./data_epicenter_labels.txt'))
k = 4
from numpy import *
centroids,clusterAssment = kMeans(datMat,k)
print('带标签训练质心:')
print(centroids)
centroids1,clusterAssment1 = kMeans(datMat1,k)
print('b不带标签训练质心:')
print(centroids1)
# to read the image stored in the working directory
data = image.imread('地图.png')
plt.figure(1)
plt.imshow(data,extent=(0, data.shape[1], 0, data.shape[0]))
x = list((datMat1)[:,0])
print(x)
y = list((datMat1)[:,1])
plt.scatter(x, y,c='red', s=10,)
'''
showCluster(datMat[:,0:2],k,centroids,clusterAssment)
plt.figure(2)
showCluster(datMat1[:,0:2],k,centroids1,clusterAssment1)
'''
plt.show()
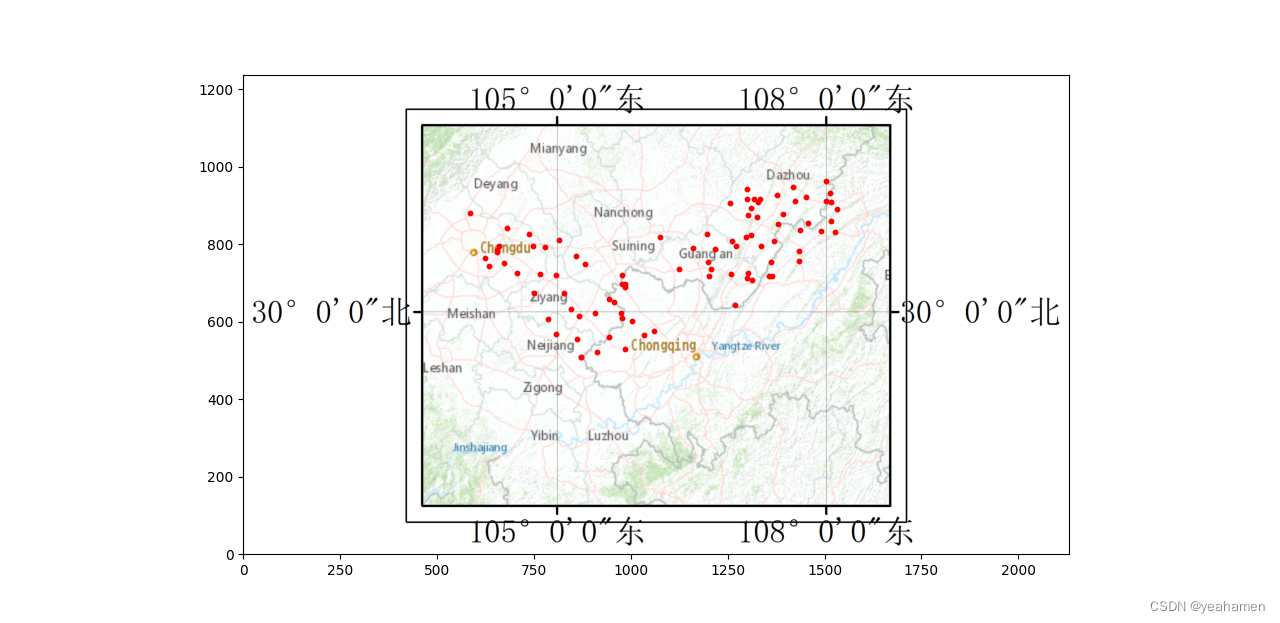
然后用聚类的方法求实际最大可能的震中位置即可