2023贵工程团体程序设计赛

这是一道数学题？

道路有两边。

#include<bits/stdc++.h>
using namespace std;
int main(){
    int n,m;
    cin>>n>>m;
    cout<<(n/m+1)*2;
	return 0;
}

CPA的团体赛

直接输出。

#include <bits/stdc++.h>
using i64 = long long;
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(nullptr)
int main()
{
IOS;
std::cout << "Welcome to the CPA team competition. I hope you all have AK.\n";
return 0;
}

这是一道输出题。

转译。

#include<bits/stdc++.h>
using namespace std;
int main(){
	 cout<<"CPA\\n最棒！";
	return 0;
}

D	CPA会长有多少个字符串

map或者set。

#include <bits/stdc++.h>
using i64 = long long;
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(nullptr)
int main()
{
IOS;
int n;
std::cin >> n;
std::set <std::string> se;
while (n --){
std::string s;
std::cin >> s;
se.insert(s);
}
std::cout << se.size() << "\n";
return 0;
}

我爱打乒乓球

数学。

//代码1：模拟
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,x=0,y=0;
	cin>>n;
	if(n<=0)cout<<"0 0";//该测试点为坑点
    else {
	while(n!=1){
		x+=n/2;
	    if(n%2)n=n/2+1;
	    else n=n/2;
		y++;
	}cout<<y<<' '<<x;}
	return 0;
}

//代码2：数学思维
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,x=0,y=0;
	cin>>n;
	if(n<=0)cout<<"0 0";
	else{
	for(int i=0;i<=n/2;i++)
	if(pow(2,i)>=n){
		y=i;break;
	}cout<<y<<' '<<n-1;}
	return 0;
}

我爱找规律

隔项加3。

//代码1：模拟
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,a[1005]={0},i;
    cin>>n;
	a[1]=1;a[2]=2;
	for(i=3;i<=n;i++)a[i]=a[i-2]+3;
	cout<<a[n];
	return 0;
}

//代码2：数学思维。
#include<bits/stdc++.h>
using namespace std;
int main(){
	int n,x=0;
    cin>>n;
	if(n%2==1)x=n*3/2;
	else x=n*3/2-1; 
	cout<<x;
	return 0;
}

cpa我来了！

map的应用、string的find函数以及大小写字符转换。

#include<bits/stdc++.h>
using namespace std;
int main(){
	 string s;
	 map<char,int>a;
	 getline(cin,s);
	 for(int i=0;i<s.size();i++){
	 	a[s[i]]++;
	 }
	 for(int i=0;i<=127;i++){
	 	if(a[char(i)]!=0)cout<<char(i)<<':'<<a[char(i)]<<endl;
	 }
	 for(int i=0;i<s.size();i++){
        if(s[i]>='A'&&s[i]<='Z'){
            s[i]=tolower(s[i]);
            //s[i]+=32;
            //s[i]=s[i]-'A'+'a';
        }
    }
	 if(s.find("cpa")!=-1)cout<<"^_^";
	 else cout<<"T_T";
	return 0;
}

520还是250？

循环。

#include<bits/stdc++.h>
using namespace std;
int main(){
        string s;int i,j,k,x=0,y=0;
        cin>>s;
        for(i=0;i<s.size();i++){
        	for(j=i+1;j<s.size();j++){
        		for(k=j+1;k<s.size();k++){
        			if(s[i]=='5'&&s[j]=='2'&&s[k]=='0')x++;
        			if(s[i]=='2'&&s[j]=='5'&&s[k]=='0')y++;
				}
			}
		}
		cout<<x<<" "<<y<<endl;
		if(x>y)cout<<"Yes";
		else cout<<"No";
	return 0;
}

KK的二进制串

将字符串L，R分别转成对应的十进制，再求L(10) ^ R(10)。

#include <iostream>
using namespace std;
typedef long long LL;
LL qmi(LL a, LL b)
{
LL res = 1;
while (b)
{
if (b & 1) res *= a;
a *= a;
b >>= 1;
}
return res;
}
LL get(string str)
{
LL w = 1, res = 0;
for (int i = str.size() - 1; ~i; i -- ,w *= 2) if (str[i] == '1') res += w;
return res;
}
int main()
{
string l, r;
cin >> l >> r;
LL a = get(l), b = get(r);
LL c = qmi(a, b);
cout << a << ' ' << b << ' ' << c << endl;
return 0;
}

灵活走位

题目其实已经很明确的表示了这就是一个N皇后问题，我们只需要DFS一下就可以解决。从问题分析，每一次走了之后的点需要记录的信息有行，列，左斜线，右斜线。因为我们是一行一行枚举的，所以可以直接不用记录行信息，接着我们可以找到一个规律，一条左斜线上的点的坐标（x,y）满足x+y为一个固定的值，那么我们可以把这个值作为唯一确定左斜线的标识。同理可得右斜线满足x+(n-y)为一个固定值，所以我们可以把这个值作为确定右斜线的唯一标识。那么我们每次DFS的时候就把列，两个斜线标记为用过并且继续往下找直到找到第N+1层就表示我们找到了一组解，之后再往后退并且消除标记就可以了。

#include<bits/stdc++.h>
using namespace std;
int n,a[20],sum,r,t;
bool b[20],c[20],d[20];//b行,c,d斜线
void dfs(int i)
{
    int j;
    if(i>n) sum++;
    for(j=1;j<=n;j++)
    {
    	if(!b[j]&&!c[i+j]&&!d[i-j+n])
      	{
         	a[i]=j;
         	b[j]=1;
         	c[i+j]=1;
         	d[i-j+n]=1;
			dfs(i+1);
         	b[j]=0;
			c[i+j]=0;
         	d[i-j+n]=0; 
      	}
	}	
}
int main()
{
	cin>>n;
	dfs(1);
	cout<<sum<<endl;
	return 0;
}

出什么题目呢？

结构体排序加循环输出图形。

#include<bits/stdc++.h>
using namespace std;
struct xx{
	int x, y;
}s[20];
bool cmp(xx a,xx b){
	if(a.y==b.y)return a.x<b.x;
	return a.y<b.y;
} 
int main(){
	int n,i,j,k=0,b;
	cin>>n;
	b=sqrt(n);
	for(i=0;i<n;i++)cin>>s[i].x>>s[i].y;
	sort(s,s+n,cmp);
	for(i=1;i<=b;i++){
		for(j=1;j<=3*(b-i);j++)cout<<' ';
		for(j=1;j<=2*i-1;j++){
			if(j!=1)cout<<' ';
			 printf("%02d",s[k++].x);
		}
		cout<<endl;
	}
	return 0;
}

相同教室的朋友

对于这个题目我们很轻松就能看出来这是一道并查集的题，所以我们直接套用并查集模板，只是在处理的时候先判断x等不等于y，如果等于就直接输出?，此处应该小心中英文下的问号不一样。如果x!=y就调用并查集的find函数来看是否在同一个联通集里面，如果在就输出Yes否则就输出No。

#include<bits/stdc++.h>
using namespace std;
int n,m,a[5001],p;

int find(int x)
{
	if(x==a[x]) return x;
	else return a[x]=find(a[x]);
}

int main()
{
	cin>>n>>m>>p;
	for(int i=1;i<=n;i++)
		a[i]=i;
	int x,y;
	for(int i=1;i<=m;i++)
	{
		cin>>x>>y;
		a[find(x)]=find(y);
	}
	for(int i=1;i<=p;i++)
	{
		cin>>x>>y;
		if(x==y){cout<<"?\n";continue;}
		int xx=find(x),yy=find(y);
		if(xx==yy) cout<<"Yes"<<endl;
		else cout<<"No"<<endl;
	}
	return 0;	
}

CPA会长查询

前缀和+数学推理

#include <bits/stdc++.h>
using i64 = long long;
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(nullptr)
int main()
{
IOS;
i64 n, q;
std::cin >> n >> q;
std::vector <i64> a(n + 1), s(n + 1);
int sum = 0;
for (int i = 1; i <= n; i ++){
std::cin >> a[i];
sum += a[i];
}
for (i64 i = 1; i <= n; i ++){
s[i] = s[i - 1] + a[i];
}
while (q --){
i64 l, r, x;
std::cin >> l >> r >> x;
i64 ans = sum - (s[r] - s[l - 1]) + (r - l + 1) * x;
if (ans & 1){
std::cout << "YES\n";
}else {
std::cout << "NO\n";
}
}
return 0;
}

CPA会长买图书

01分数规划+二分答案

#include<bits/stdc++.h>
using i64 = long long;
#define IOS std::ios::sync_with_stdio(false), std::cin.tie(nullptr)
const int N = 1e4 + 10;
int n, k;
struct em{
int c, v;
i64 sum;
}f[N];
bool cmp(em a, em b){
return a.sum > b.sum;
}
i64 check(i64 x){
i64 res = 0, vs = 0, cs = 0;
for (int i = 1; i <= n; i ++){
f[i].sum = f[i].v - x * f[i].c;
}
std::sort(f + 1, f + 1 + n, cmp);
for (int i = 1; i <= k; i ++){
res += f[i].sum;
if (res < 0){
return -1;
}
vs += f[i].v;
cs += f[i].c;
}
return vs / cs;
}
void solve(){
std::cin >> n >> k;
for (int i = 1; i <= n; i ++){
std::cin >> f[i].c >> f[i].v;
}
int l = 0, r = 1e8 + 10;
i64 ans = 0;
while (r > l){
int mid = l + r >> 1;
i64 res = check(mid);
if (res == -1){
r = mid;
}else {
ans = res;
l = mid + 1;
}
}
std::cout << ans << "\n";
}
int main()
{
 IOS;
int t = 1;
std::cin >> t;
while (t --){
solve();
}
 return 0;
}

天才界灵师小K

使用二分图矩阵建图方式建图

对于每个点

与它周围 4 个点进行连边边权为无穷大

a d

S b e T

c f

S T 为源点汇点 S 连向与连向 T 的边为边权

答案 1 = 删除点的和

答案 2 = 总价值 - 删除点的和

要使取出总和最大，就是使删除点的和最小

即删除一些边使集合分为 2 部分使他们不连通

就是最大独立集：总价值 - 最小覆盖集

本题考查的的为最小割模型中的最大独立集

#include <iostream>
#include <cstring>
#include <algorithm>
using namespace std;
const int N = 10010, M = N << 1, INF = 1e9;
int n, m, S, T;
int h[N], e[M], ne[M], f[M], idx;
int d[N], q[N], cur[N];
int dx[] = {-1, 0, 1, 0}, dy[] = {0, 1, 0, -1};
int get(int i, int j)
{
return (i - 1) * m + j;
}
void add(int a, int b, int c)
{
e[idx] = b, f[idx] = c, ne[idx] = h[a], h[a] = idx ++;
e[idx] = a, f[idx] = 0, ne[idx] = h[b], h[b] = idx ++;
}
bool bfs()
{
int hh = 0, tt = 0;
memset(d, -1, sizeof d);
q[tt ++ ] = S, cur[S] = h[S], d[S] = 0;
while (hh < tt)
{
int t = q[hh ++ ];
for (int i = h[t]; ~i; i = ne[i])
{
int ver = e[i];
if (d[ver] == -1 && f[i])
{
d[ver] = d[t] + 1;
cur[ver] = h[ver];
if (ver == T) return true;
q[tt ++ ] = ver;
}
}
}
return false;
}
int find(int u, int limit)
{
if (u == T) return limit;
int flow = 0;
for (int i = cur[u]; ~i && flow < limit; i = ne[i])
{
cur[u] = i;
int ver = e[i];
if (d[ver] == d[u] + 1 && f[i])
{
int t = find(ver, min(f[i], limit - flow));
if (!t) d[ver] = -1;
f[i] -= t, f[i ^ 1] += t, flow += t;
}
}
return flow;
}
int dinic()
{
int r = 0, flow;
while (bfs()) while (flow = find(S, INF)) r += flow;
return r;
}
int main()
{
scanf ("%d%d", &n, &m);
S = 0, T = n * m + 1;
memset(h, -1, sizeof h);
int tot = 0;
for (int i = 1; i <= n; i ++ )
for (int j = 1; j <= m; j ++ )
{
int w;
scanf ("%d", &w);
if (i + j & 1)
{
add(S, get(i, j), w);
for (int k = 0; k < 4; k ++ )
{
int a = dx[k] + i, b = dy[k] + j;
if (a < 1 || a > n || b < 1 || b > m) continue;
add(get(i, j), get(a, b), INF);
}
}
else add(get(i, j), T, w);
tot += w;
}
int res = dinic();
printf ("%d %d\n", res, tot - res);
return 0;
}

近在眼前

#include<bits/stdc++.h>
using namespace std;
int n,m;

long long mi(long long a,int b)
{
	long long cnt=1;
	while(b)
	{
		if(b&1) cnt*=a;
		a*=a;
		b>>=1;		
	}
	return cnt;
}

int main()
{
	cin>>n>>m;
	if(m==1)
	{
		cout<<1<<endl;
		return 0;
	}
	int t=m;
    long long ans=1;
    for(int i=2;i*i<=m;i++)
    {
        if(m%i==0)
        {
            ans*=mi(i,n)-1;
			t/=i;
            while(m%i==0)  m/=i;
        }
    }
    if(m!=1)
	{
		ans*=(mi(m,n)-1);
		t/=m;
	}
    ans=ans*mi(t,n);
    cout<<ans<<endl;
	return 0;
}

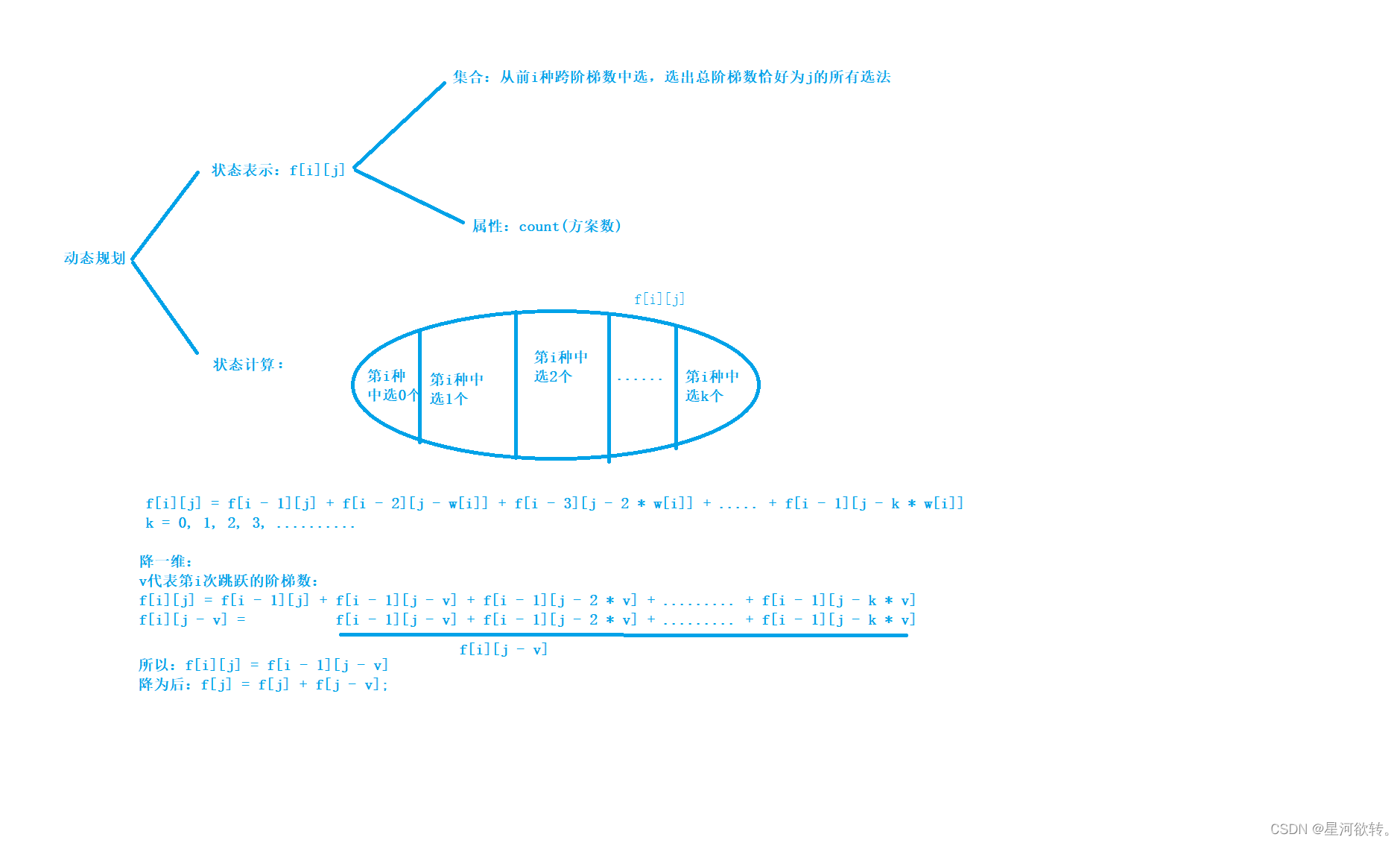
九层宝塔

推出状态转移方程：

在本题中有限制最少要两两组合，所以 V 只需要枚举到 n - 1

#include <iostream>
#include <cstring>
using namespace std;
const int N = 12010, mod = 1e9 + 7;
int n;
int v[N];
int f[N];
int main()
{
cin >> n;
for (int i = 1; i < n; i ++ ) v[i] = i;
f[0] = 1;
for (int i = 1; i < n; i ++ )
for (int j = v[i]; j <= n; j ++ )
f[j] = (f[j] + f[j - v[i]]) % mod;
cout << f[n] << endl;
return 0;
}