一、K近邻算法

二、决策树

1.一些原理介绍

2.决策树案例与实践

三、距离

一、K近邻算法

我们引入accuracy_score，利用score()的方法评估准确性。k近邻算法中的k是一个超参数，需要事先进行定义。

k值得选取经验做法是一般低于训练样本得平方根。当然，k值得选取也不是越大越好，根据某些实验得结果表明，k值得增加反而会导致准确率的下降。这里我们选择k=5进行分析：

#导入库
from sklearn import datasets
from sklearn.model_selection import train_test_split
from sklearn.neighbors import KNeighborsClassifier
from sklearn.metrics import accuracy_score

#加载数据
iris=datasets.load_iris()  #创建iris的数据，把属性存在X，类别标签存在y
X=iris.data
y=iris.target

#划分训练集和测试集
X_train,X_test,y_train,y_test=train_test_split(X,y,test_size=0.3,random_state=1)

#K近邻算法
model=KNeighborsClassifier(n_neighbors=5)  #指定k=5
model.fit(X_train,y_train)

#显示结果
y_pred=model.predict(X_test)
train_score=model.score(X_train,y_train)
test_score=model.score(X_test,y_test)
print(y_pred)
print(y_test)
print("训练集的准确率：%f"%train_score)
print("测试集的准确率：%f"%test_score)
print(accuracy_score(y_pred,y_test))  #评估拟合的准确性

二、决策树

1.一些原理介绍

信息所能传递的信息量与该信息的不确定性之间有着显著的关系。因此，如果关注信息量，就需要能对其进行合理的度量。在信息论中，熵正式针对随即信息的这种不确定性（也称不纯度）进行度量。变量的不确定性越大，则说明需要了解的信息就越多，熵的值就会越大。

决策时就是利用这种信息熵的思想来衡量数据划分的优劣，从而让划分后的信息能够获得的信息量最大。什么是信息熵呢？它是一种度量样本集合纯度的常用指标之一。

假如一个数据集当中有k类样本，每类样本的占比为 $p_{i}\left ( i=1,\cdots ,k \right )$ ，则信息熵为：

$H(y)=-\sum_{i=1}^{k}p_{i}\log_{2}p_{i}$

其中，对数的底为2，表示信息熵的单位为比特，H(y)的值越小，则数据集的纯度越高。

当p=0或p=1时，H(y)=0，随机变量完全没有不确定性。

当具备衡量数据集纯度的度量指标信息熵之后，下一步需要了解一个重要的概念——信息增益。信息增益与描述变量的特征关系十分密切，通过信息增益的方式，可以找出哪个特征（当存在多个特征时）对样本的信息增益最大，因此，也就可以利用信息增益帮助决策树选择特征。信息增益是待分类的集合的熵和选定某个特征的条件熵之差。

2.决策树案例与实践

我们用一个具体的案例说明信息增益的工作原理，这里选择Weka数据集中的天气数据，如下图所示，数据中给出了四个特征与决策（分类）。

天气数据
编号	天气展望	温度	湿度	是否有风	是否出游
1	晴天	炎热	高	无	否
2	晴天	炎热	高	有	否
3	阴天	炎热	高	无	是
4	雨天	温暖	高	无	是
5	雨天	寒冷	正常	无	是
6	雨天	寒冷	正常	有	否
7	阴天	寒冷	正常	有	是
8	晴天	温暖	高	无	否
9	晴天	寒冷	正常	无	是
10	雨天	温暖	正常	无	是
11	晴天	温暖	正常	有	是
12	阴天	温暖	高	有	是
13	阴天	炎热	正常	无	是
14	雨天	温暖	高	有	否

根据历史数据可以得知14天内有9天选择外出，5天没有外出，此时的信息熵为：

$-(\frac{9}{14}\log_{2}\frac{9}{14}+\frac{5}{14}\log_{2}\frac{5}{14})=0.940$

以天气展望特征开始计算信息增益，下面给出了该特征下不同情形的信息熵：

晴天信息熵： $-(\frac{2}{5}log_{2}\frac{2}{5}+\frac{3}{5}log_{2}\frac{3}{5})=0.971$

阴天信息熵： $-(\frac{4}{4}log_{2}\frac{4}{4}+\frac{0}{4}log_{2}\frac{0}{4})=0$

雨天信息熵： $-(\frac{3}{5}log_{2}\frac{3}{5}+\frac{2}{5}log_{2}\frac{2}{5})=0.971$

因为晴天、阴天、雨天的比例分别是 $\frac{5}{14}$ ， $\frac{4}{14}$ 和 $\frac{5}{14}$ ，所以天气属性下的信息熵为： $\frac{5}{14}\times 0.971+\frac{4}{14}\times 0+\frac{5}{14}\times 0.971=0.694$ 。这就是天气展望特征下的条件熵。因此，天气展望属性下的信息增益为：0.940-0.694=0.246。

同理，可以计算处出温度特征下的信息增益为0.029，湿度特征下的信息增益为0.152，是否有风特征下信息增益为0.048。

比较不同特征，可以看到天气展望特征下信息增益最大，因此该特征被首先用来进行划分集合。

决策树算法对每个分支节点所包含的样本集利用其他特征（不再包含天气展望特征）再做进一步的划分，过程与上述原理类似，这里不再赘述。

除了信息熵以外，基尼不纯度也常常用来衡量信息的纯度，一些图书或者资料中也译为基尼系数、基尼杂质等。

基尼不纯度是一种用于构建决策树的测量方法，用于确定数据集的特征应该如何分割节点以形成决策树。更准确地说，数据集的基尼不纯度是一个介于0~0.5之间的数字，它表示如果根据数据集中的类分布给心得随机数据一个随机的类标签，它被错误分类的可能性。其公式如下：

$Gini(y)=\sum_{i=1}^{k}p_{i}(1-p_{i})=1-\sum_{i=1}^{k}p_{i}^{2}$

其中，k的含义与前文信息熵的含义一样，代表样本类的数量。

决策树相比于其他算法，更容易出现过拟合的情形，因为它过分迎合每一个训练的数据，因此导致泛化能力较低。

过拟合是指模型分析的结果与训练数据过于接近，甚至完全对应，因此可能无法适应更多的数据或可靠地预测未来的观察结果。通常，过拟合是指一个数学模型包含的参数超过了数据所能证明的范围。

剪枝法是一种常用的缓解决策树过拟合问题的方法。在Scikit-learn库中通过限制树高达到这种‘剪枝“的目的。利用max_depth限制树的最大深度，超过设定深度的树枝会被全部剪掉。

因为随着决策树高不断增加，对数据量的需求也在增加，否则容易导致过拟合的出现，因此限制树高本身也能够有效抑制过拟合的发生。

在进行决策树建模时，可以将准则criterion设置为使用熵还是基尼不纯度。

#导入库
import numpy as np
import random
from sklearn.datasets import load_iris
from sklearn import tree
from sklearn.metrics import accuracy_score

#加载数据
data=load_iris()

#划分训练集与测试集
#随机生成不重复的45个0~149的整数（相当于总体）
random.seed(1)
idx_test=random.sample(range(0,149),45)

#训练集
X_train=np.delete(data.data,idx_test,axis=0)
y_train=np.delete(data.target,idx_test)

#测试集
X_test=data.data[idx_test]
y_test=data.target[idx_test]

#决策树
model=tree.DecisionTreeClassifier(max_depth=4,criterion='entropy')  #可将;'entropy'替换成'gini'
model.fit(X_train,y_train)

#输出测试结果
train_score=model.score(X_train,y_train)
test_score=model.score(X_test,y_test)
print("训练集得到准确率：%f"%train_score)
print("测试集的准确率：%f"%test_score)
print("测试集中实际值：",y_test)
print("利用模型预测值：",model.predict(X_test))

决策树的可视化是其显著的优势之一。为了实现可视化，我们要在Jupyter中安装Graphivz库并调用。

#可视化，将结果保存至pdf文件
import graphviz
dot_data=tree.export_graphviz(model,out_file=None,feature_names=data.feature_names,
                             class_names=data.target_names,filled=True,rounded=True,
                             special_characters=True)
graph=graphviz.Source(dot_data)
graph.render("iris_tree")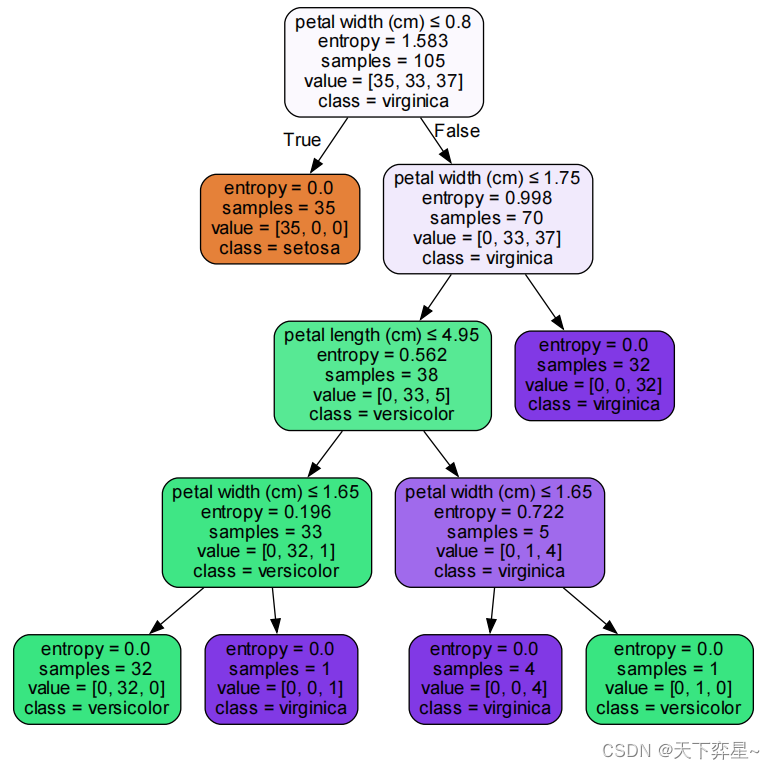

以根节点为例，数据所代表的含义：

第一行petal length(cm)<=2.35表示鸢尾花数据集中“花瓣长”小于等于2.35(cm)的时候，走左下边的子树，否则走右下边子树。

第二行entropy=1.583，表示当前信息熵的值。

第三行samples=105，samples表示当前的样本数。鸢尾花数据集中有150条数据，因为选择45个测试样本，训练集则为105个样本。

第四行value表示属于该节点的每个类别的样本个数，value是一个数组，数组中的元素之和为样本的值。鸢尾花数据集中有3个类别，分别为；山鸢尾(setosa)、变色鸢尾(versicolor)和维吉尼亚鸢尾(virginica)。因此，在value中的数字分别依次表示这三种不同类型鸢尾花的数量。

第五行class主要显示出容量多的样本维吉尼亚鸢尾。

决策树是一种渴望学习的方法，而K近邻算法是懒惰学习。渴望学习在估计测试数据之前其实就已经开始学习了，因此可以快速进行预测。懒惰学习则是等到测试数据来时才开始学习，因此预测起来相对较慢。

三、距离

已知两个点的坐标分别为： $A(x_{1},y_{1})$ 和 $B(x_{2},y_{2})$ ，则：

欧式距离： $d=\sqrt{(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^2}$

曼哈顿距离： $d=|x_{2}-x_{1}|+|y_{2}-y_{1}|$

切比雪夫距离： $d=max(|x_{2}-x_{1}|,|y_{2}-y_{1}|)$

假设平面熵有高维空间A(1,2,3,4,5)和B(10,9,8,7,6)两点，使用scipy库可以方便求解出以上三种距离，代码如下：

import numpy as np
A=([1,2,3,4,5])
B=([10,9,8,7,6])
from scipy.spatial.distance import pdist
X=np.vstack([A,B])
d_E=pdist(X)  #欧氏距离
d_M=pdist(X,'cityblock')  #曼哈顿距离
d_C=pdist(X,'chebyshev')  #切比雪夫距离
print("欧氏距离=",d_E,"曼哈顿距离=",d_M,"切比雪夫距离=",d_C)