🍑 算法题解专栏

---

🍑 排书

给定 $n$ 本书，编号为 $1\sim n$。

在初始状态下，书是任意排列的。

在每一次操作中，可以抽取其中连续的一段，再把这段插入到其他某个位置。

我们的目标状态是把书按照 $1\sim n$ 的顺序依次排列。

求最少需要多少次操作。

输入格式

第一行包含整数 $T$，表示共有 $T$ 组测试数据。

每组数据包含两行，第一行为整数 $n$，表示书的数量。

第二行为 $n$ 个整数，表示 $1\sim n$ 的一种任意排列。

同行数之间用空格隔开。

输出格式

每组数据输出一个最少操作次数。

如果最少操作次数大于或等于 $5$ 次，则输出 5 or more。

每个结果占一行。

数据范围

$1\le n\le 15$

输入样例：

3
6
1 3 4 6 2 5
5
5 4 3 2 1
10
6 8 5 3 4 7 2 9 1 10

输出样例：

2
3
5 or more

---

🍑 dfs迭代加深 + A*

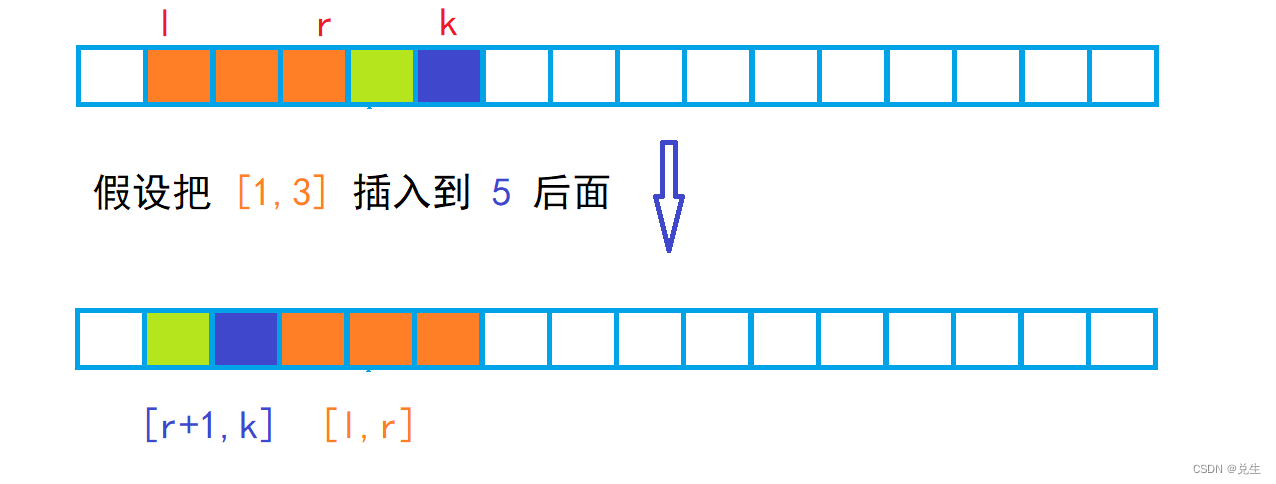
🍑 插入过程实现思路

import java.util.Arrays;
import java.util.Scanner;

public class Main
{
	static int N = 15, n;
	static int q[] = new int[N];
	static int[][] w = new int[5][N];// 备份数组，保存没一层的序列

	/**
	 * 估价函数
	 * 
	 * @return 返回后继数非逐一递增的情况个数
	 */
	static int f()
	{
		int tol = 0;
		for (int i = 0; i + 1 < n; i++)
			if (q[i] + 1 != q[i + 1])
				tol++;
		return (tol + 2) / 3;// 每次移动至少改变三个后继，tol/3向上取整
	}

//	检查序列是否合法（单调逐一递增）
	static boolean check()
	{
		for (int i = 0; i + 1 < n; i++)
			if (q[i] + 1 != q[i + 1])
				return false;
		return true;
	}

	/**
	 * @param u    表示当前搜索到的层数
	 * @param mdep 表示最大搜索层数
	 * @return
	 */
	static boolean dfs(int u, int mdep)
	{
		// 当前层数 + 到达目的地最小需要的评估步数 > 最大搜索层数
		if (u + f() > mdep)
			return false;
//		成功搜到答案直接返回
		if (check())
			return true;

		for (int len = 1; len <= n; len++)// 枚举连续序列的长度
			for (int l = 0; l + len - 1 < n; l++)// 枚举序列的左端点
			{
				int r = l + len - 1;// 计算区间右端点的位置
				// 枚举将序列插入到后面的哪个数 的后面
				for (int k = r + 1; k < n; k++)// 只枚举后边的坑位（组合式枚举）
				{
					// w[u]存未修改前的当前层状态
					w[u] = Arrays.copyOf(q, q.length);// q --> w
					int idx = l;// idx枚举变动后区间的下标
					for (int x = r + 1; x <= k; x++)// 后边的先移到前边去
						q[idx++] = w[u][x];
					for (int x = l; x <= r; x++)// 再把待插入序列放在后边
						q[idx++] = w[u][x];

					if (dfs(u + 1, mdep))
						return true;
					q = Arrays.copyOf(w[u], w[u].length);// w --> q
				}
			}
		return false;
	}

	public static void main(String[] args)
	{
		Scanner sc = new Scanner(System.in);
		int T = sc.nextInt();
		while (T-- > 0)
		{
			n = sc.nextInt();
			for (int i = 0; i < n; i++)
				q[i] = sc.nextInt();

			int mdep = 0;// 迭代加深的最大搜索层数
			while (mdep < 5 && !dfs(0, mdep))
				mdep++;
			if (mdep >= 5)
				System.out.println("5 or more");
			else
				System.out.println(mdep);
		}
	}
}

👨‍🏫 ypuyu的题解