描述
给一个长度为n链表,若其中包含环,请找出该链表的环的入口结点,否则,返回null。
数据范围: n≤10000n≤10000,1<=结点值<=100001<=结点值<=10000
要求:空间复杂度 O(1)O(1),时间复杂度 O(n)
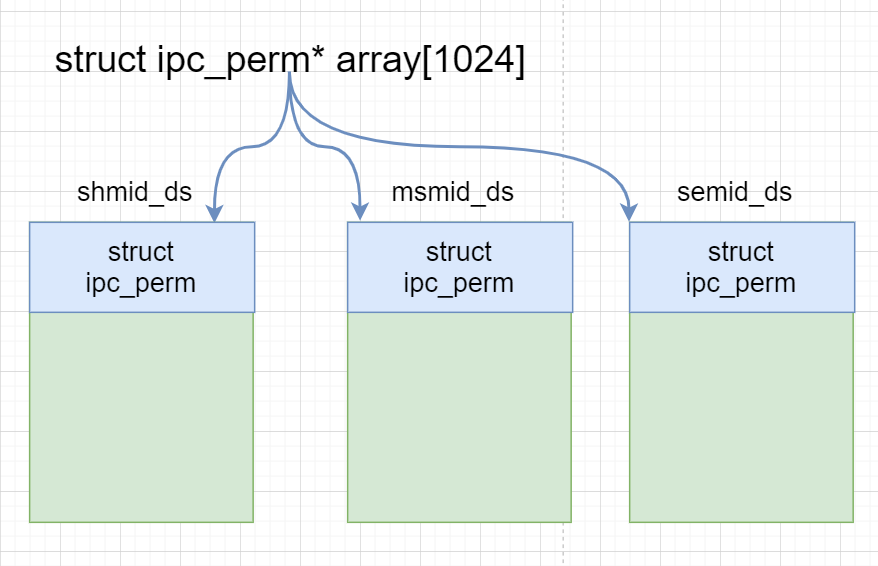
例如,输入{1,2},{3,4,5}时,对应的环形链表如下图所示:
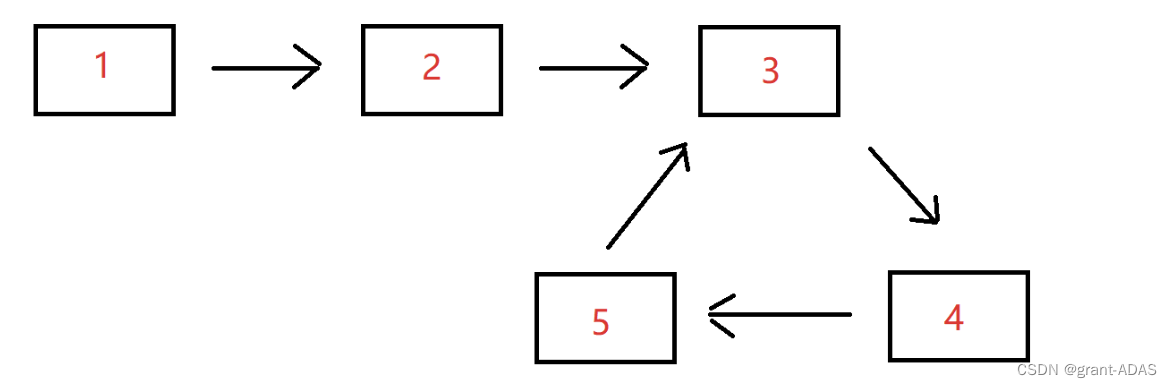
可以看到环的入口结点的结点值为3,所以返回结点值为3的结点。
输入描述:
输入分为2段,第一段是入环前的链表部分,第二段是链表环的部分,后台会根据第二段是否为空将这两段组装成一个无环或者有环单链表
返回值描述:
返回链表的环的入口结点即可,我们后台程序会打印这个结点对应的结点值;若没有,则返回对应编程语言的空结点即可。
示例1
输入:{1,2},{3,4,5}
返回值:3
说明:返回环形链表入口结点,我们后台程序会打印该环形链表入口结点对应的结点值,即3
示例2
输入:{1},{}
返回值:"null"
说明:没有环,返回对应编程语言的空结点,后台程序会打印"null"
示例3
输入:{},{2}
返回值:2
说明:环的部分只有一个结点,所以返回该环形链表入口结点,后台程序打印该结点对应的结点值,即2
算法1(哈希集合)
解题思路:
一个直观的想法就是用哈希表存下我们从链表头往下走路径所见过的节点指针,当出现已经记录过的节点时,这个节点就是环的入口节点
代码实现(C++11)
/*
struct ListNode {
int val;
struct ListNode *next;
ListNode(int x) :
val(x), next(NULL) {
}
};
*/
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
unordered_set<ListNode*> st;
while (pHead) {
if (st.count(pHead)) {
return pHead; // 若已经记录过,直接返回
}
st.insert(pHead); // 记录当前结点
pHead = pHead->next;
}
return nullptr; // 无环
}
};
时间复杂度:O(n), n为链表长度,遍历一次链表的时间复杂度为O(n)
空间复杂度:O(n),哈希集合所用的空间
算法2(快慢指针)
解题思路
我们知道,用快慢指针可以很容易判断一条链表是否存在环,快指针fast每次走两步,慢指针slow每次走一步,那么若进入环中,每次他们之间的相对距离都会-1,直到两者相遇。虽然这能很快的知道是否存在环,但是它能否帮我们找到环的入口呢,答案是肯定的
假设从头节点到环的入口节点的前一个节点一共有a个,环中的节点有b个,设fast指针走过的节点数是f,slow指针走过的节点数是s,那么有以下两个结论:
f = 2 * s (即快指针走过的节点数一定是慢指针的两倍)
f = s + nb (当两者相遇时,快指针一定已经绕环走了n圈)
由上面两个等式可以得出,f = 2nb,s = nb
故可知,两指针相遇时,慢指针已经走了nb步,已知我们要走到入口节点,需要走a + kb步,而这时s = nb只要再走a即可到达入口,我们把快指针移动到头节点,然后两个指针一步一步往后走,当它们相遇时所处的位置就是入口节点
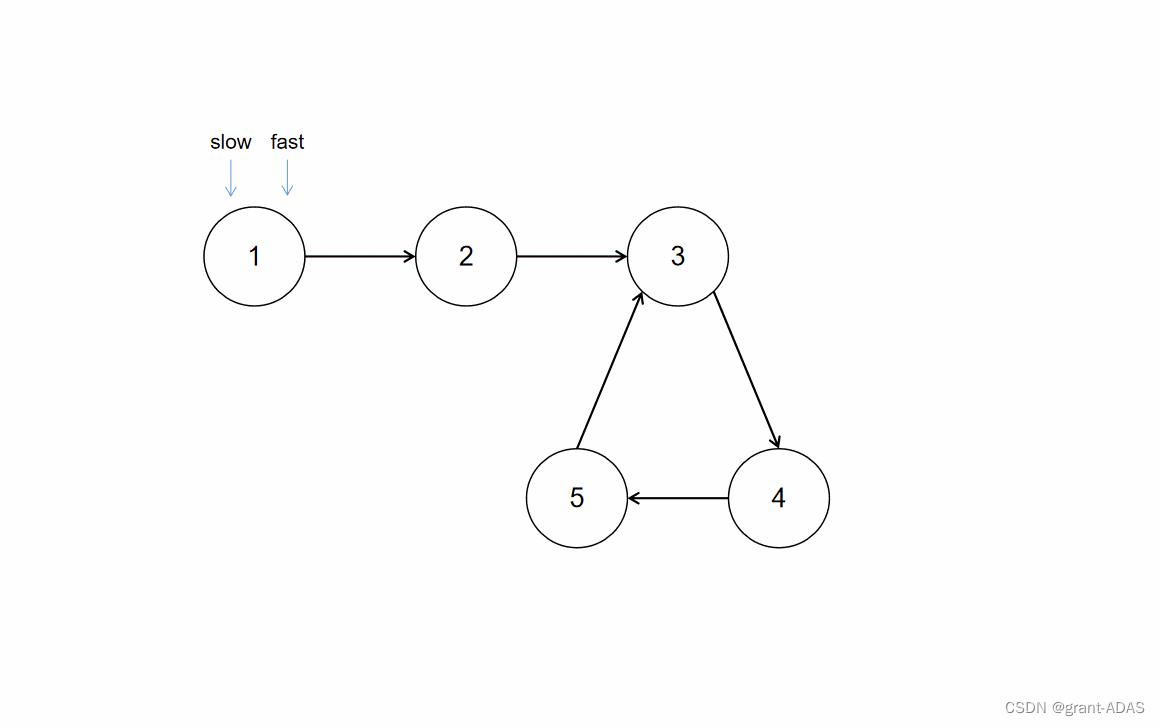
代码实现(C++11)
class Solution {
public:
ListNode* EntryNodeOfLoop(ListNode* pHead) {
ListNode *fast = pHead, *slow = pHead; // 快慢指针一开始都指向头
while(fast){
slow = slow->next; // 慢指针走一步
if(fast->next == nullptr) return nullptr; // 若快指针的下一步不能走,则说明两指针不会相遇
fast = fast->next->next; // 快指针向后走两步
if(fast == slow){ // 找到相交节点, 此时慢指针已经走了nb步
fast = pHead; // 快指针重新移动到头
while(fast != slow){ // 直到两指针相遇位置,每次向后走一步
fast = fast->next;
slow = slow->next;
}
return fast; // 找到入口节点,直接返回
}
}
return nullptr;
}
};