文章目录
- Part.I Introduction
- Part.II 概念比较
- Chap.I 序贯最小二乘平差
- Chap.II 卡尔曼滤波
- Chap.III 比较
- Reference
Part.I Introduction
序贯最小二乘平差和卡尔曼滤波有些相似,但是还是有一些区别:
- 序贯最小二乘平差用来处理静态数据,也就是说待估参数不随时间发生变化;卡尔曼滤波可以处理动态数据,也就是说待估参数随着时间而发生改变。
- 序贯最小二乘平差忽略了待估参数的先验方差信息,将其作为非随机参数进行处理;卡尔曼滤波考虑到了待估参数的先验方差信息,将其作为随机参数进行估计。
事实上,静态逐次滤波是介于序贯最小二乘平差和卡尔曼滤波之间的参数估计方法:它和序贯最小二乘平差一样只能处理静态数据,它和卡尔曼滤波一样考虑到了待估参数的先验方差信息,将其作为随机参数进行估计。
本篇博文将序贯最小二乘平差和卡尔曼滤波放在一起进行比对,以加深对二者的理解。
Part.II 概念比较
Chap.I 序贯最小二乘平差
序贯最小二乘平差(又叫逐次相关间接平差 / 递推最小二乘平差)是对最小二乘平差的一个改进,这个改进体现在:当观测量比较多时,序贯最小二乘平差将观测值分成两组或多组,按组的顺序分别做相关间接平差,从而使其达到与两期或多期数据一起做整体平差同样的结果。
分组平差的优势:1)处理大型平差问题时,因分组平差的法方程的阶数较低,可以克服不分组时计算机容量不敷应用的困难。2)在一定情况下,例如分区平差,各组可同步进行计算,从而可以缩短计算的周期。3)当一个测量网已经完成了平差计算之后,因网形扩展或加密而增加了新的观测数据时,只需将原平差结果作为相关观测值并顾及其权逆阵,与新观测值一并进行平差,即可求得与新旧资料整体平差的相同结果。(Ref.1)

Chap.II 卡尔曼滤波
卡尔曼滤波是一种线性最小方差估计,采用动力学方程即状态方程描述被估计量的动态变化规律,被估计量的动态统计信息由激励白噪声的统计信息和动力学方程确定。其计算过程是一个不断地预测、修正的过程。在求解时不需要存储大量的观测数据,并且当得到新的观测数据时,可随时估算得新的滤波值,便于实时处理观测结果。
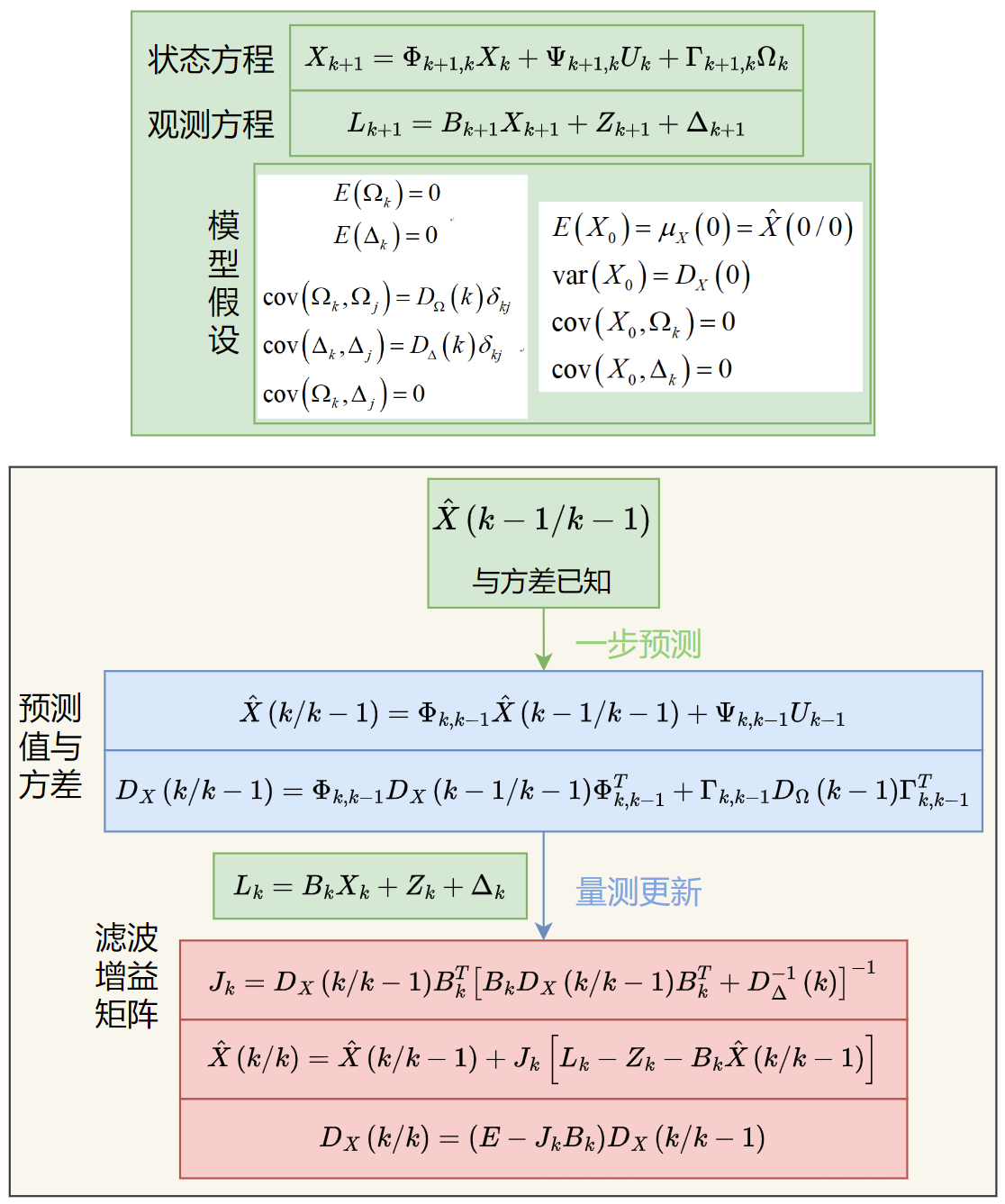
Chap.III 比较
下面是两者递推公式的比较

可以看到它们递推公式十分相似,采用递推的形式使得它们天然地适用于处理大量数据,但是它们也存在着一些区别:
- 序贯最小二乘平差用来处理静态数据,也就是说待估参数不随时间发生变化;卡尔曼滤波可以处理动态数据,也就是说待估参数随着时间而发生改变。
- 序贯最小二乘平差忽略了待估参数的先验方差信息,将其作为非随机参数进行处理;卡尔曼滤波考虑到了待估参数的先验方差信息,将其作为随机参数进行估计。
Reference
- 序贯最小二乘平差
- 严恭敏老师捷联惯导课程
- 离散线性系统的卡尔曼滤波