基本概念
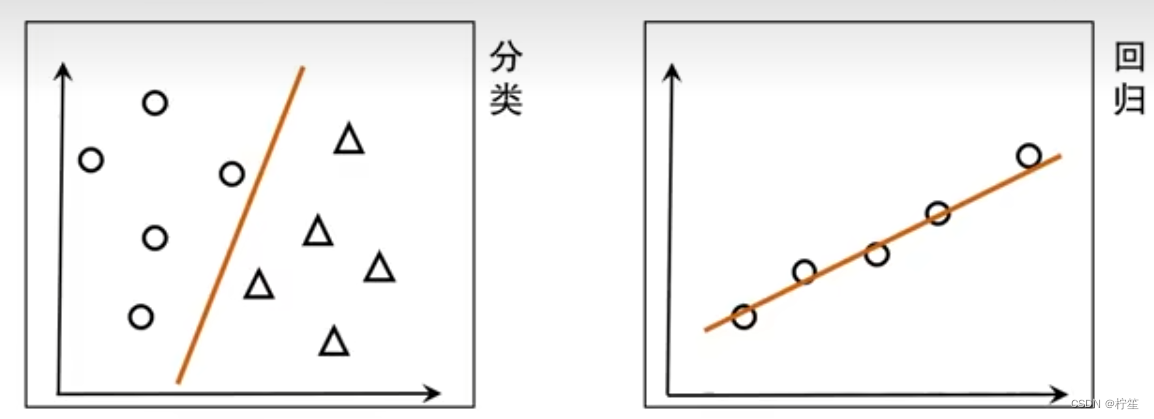
什么是回归预测?什么是分类预测?
| 模型 | 输入变量 | 预测结果 | 应用 |
|---|---|---|---|
| 回归预测 | 实值离散 | 一个连续值域上的任意值 | 预测值的分布情况 |
| 分类预测 | 实值离散 | 两个或多个分类值 | 将输入变量分类到不同类别 |
思考一个问题:分类问题是否可以转变为回归问题?
回答:当然可以!
例子:检测癌症患者患病概率,检查值可能是40%、50%、60%等连续值,但是如果我们给定一个划分标准,如高于50%的检查值认定为患病,那么我们就把一个回归问题转化成了分类问题。
什么是线性?
- 可加性,又称叠加性
- f(x+y)=f(x)+f(y)
- 齐次性,又称均匀性
- f(ax)=af(x),其中a为与x无关的常数
- f(x,y)=f(ax+by)=af(x)+bf(y)
什么是线性回归(LinearRegression)?
顾名思义:用一条线来进行回归预测。
例子:已知房屋面积和房屋价格的对应关系,100平60w;120平70w;130平75w。根据对应的散列点在二维空间描绘出来得到下图:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-M97b9Dlj-1685858452095)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230601085044975.png)]](https://img-blog.csdnimg.cn/13482802a6dd48caba0e7b465c210b54.png)
线性回归在这种背景下的工作就是寻找一条直线,尽可能的拟合这些离散点。
什么是拟合?
专业的来说:针对数据(x1,y1)、(x2,y2),…,(xn,yn),确定一个函数f(x)使得尽可能的准确表达这些变量间的关系。
拟合不一定是百分百的,如上图的这些离散点,根据两点确定一条直线的原则,你无法找到一条能够完全穿过这些点的直线,因此不同人可能会找到不同的直线,如下图:
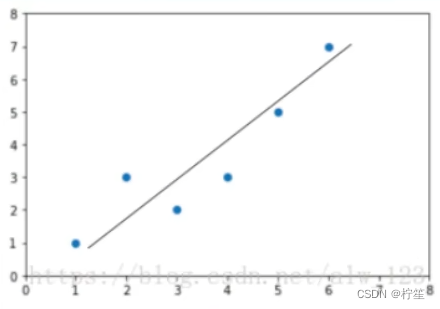
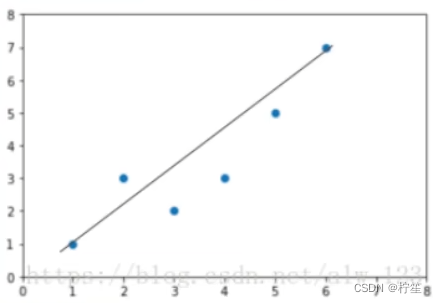
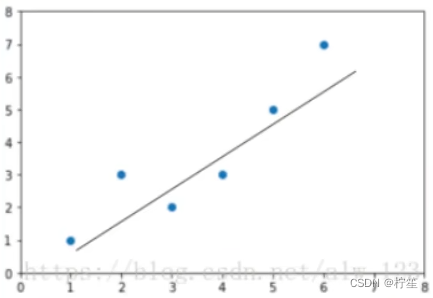
这么多条线,我们的应该选取哪一条作为最终的f(x)呢?针对这个问题,我们引入了一个评判指标——损失函数
什么是损失函数(loss function)?
首先我们明确一个概念:
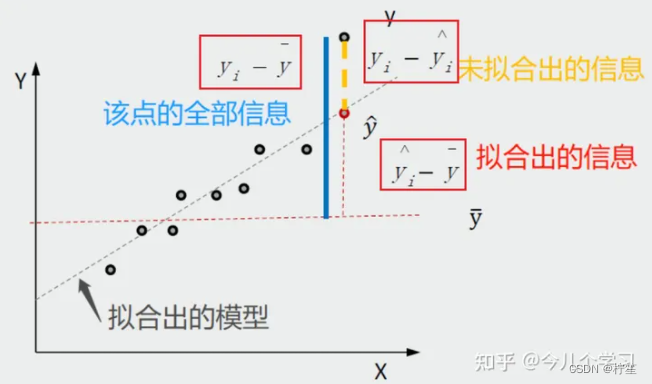
图上这条直线上的点称为预测点,图上这些离散的点称为真实点。既然是预测就会存在误差,这里我们把真实值和预测值之间的差值称为——残差
残差公式:
e
=
y
−
y
^
e = y - \hat y
e=y−y^
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-VzQhEmg3-1685858452100)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230601091424515.png)]](https://img-blog.csdnimg.cn/58d106f79da04a39b89f3d088fa4b58d.png)
对于单个具体点我们可以用残差来衡量评估标准,但对于图中所有的点,我们要进行整体评估,因此数学上一般将所有点的残差的平方加和等到一个总和
残差平方和公式(SSE):
Q
=
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
=
∑
i
=
1
n
(
y
i
−
(
β
^
0
+
β
^
1
x
i
)
)
2
Q = \sum_{i=1}^{n}(y_i-\hat y_i)^2=\sum_{i=1}^{n}(y_i-(\hat \beta_0+\hat \beta_1x_i))^2
Q=i=1∑n(yi−y^i)2=i=1∑n(yi−(β^0+β^1xi))2
我们可以通过这个SSE公式来评估我们的直线的误差,不断动态调整我们的直线,尽可能逼近最小误差
这个时候又会有另外一个疑问,误差评判标准是唯一不变的吗?
针对这个问题,马克思曾说过:要具体问题具体分析。因此损失函数的选择不是唯一的,但是有些函数常常会被我们用到,举例如下:
- 均方误差MSE
1 n ∑ i = 1 n ( y i − y ^ i ) 2 \frac{1}{n}\sum_{i=1}^{n}(y_i-\hat y_i)^2 n1i=1∑n(yi−y^i)2
- 均方根误差RMSE
1 n ∑ i = 1 n ( y i − y ^ i ) 2 \sqrt{\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat y_i)^2} n1i=1∑n(yi−y^i)2
- 平均绝对误差MAE
1 n ∑ i = 1 n ∣ y i − y ^ i ∣ \frac{1}{n}\sum_{i=1}^{n}|y_i-\hat y_i| n1i=1∑n∣yi−y^i∣
- 根均方百分比误差RMSPE
1 n ∑ i = 1 n ( y i − y ^ i y i ) 2 \frac{1}{n}\sqrt{\sum_{i=1}^{n}(\frac{y_i-\hat y_i}{y_i})^2} n1i=1∑n(yiyi−y^i)2
由于篇幅有限加上初期接触,这里不再过多拓展,更多详情在损失函数拓展篇
这个时候就会有人说,是不是我选择了一个好的损失函数,并且使其损失值最小化。我的模型就可以在工业应用中有着优秀表现呢?
答案可能是不一定的,还是那句话具体问题要具体分析,因此我们引入了另外一个评估角度——评价指标
什么是评价指标(evaluation metric)?
既然要去评价一个东西,那必须多维度全方面的去评估,因此机器学习中给出了一些常用的评价指标。
这里我们以“二分类”问题为例,所谓二分类就是把一个东西分成两类,看各自分类的正确率和错误率。
- Confusion Matrix(混淆矩阵)
| 真实情况 | 预测结果 | |
| 正例 | 反例 | |
| 正例(P) | TP(真正例) | FN(假反例) |
| 反例(N) | FP(假正例) | TN(真反例) |
- Accuracy(准确率)
真实情况和预测结果一致的样本占总样本的比例
A
c
c
u
r
a
c
y
=
T
P
+
T
N
P
+
N
Accuracy =\frac{TP+TN}{P+N}
Accuracy=P+NTP+TN
- Precision(精准率)(又称查准率)
被分为正例中真实情况为正例的比例
P
r
e
c
i
s
i
o
n
=
T
P
T
P
+
F
P
Precision =\frac{TP}{TP+FP}
Precision=TP+FPTP
- Recall(召回率)(又称查全率)
真实情况中正例被正确分类的比例
R
e
c
a
l
l
=
T
P
T
P
+
F
N
Recall =\frac{TP}{TP+FN}
Recall=TP+FNTP
- F1 Score(F1分数)
F1值是评估二元分类模型性能中精准性和召回率综合效果的指标
F
1
=
2
⋅
P
r
e
c
i
s
i
o
n
⋅
R
e
c
a
l
l
P
r
e
c
i
s
i
o
n
+
R
e
c
a
l
l
=
2
T
P
2
T
P
+
T
P
+
F
N
F_1 =\frac{2·Precision·Recall}{Precision+Recall}=\frac{2TP}{2TP+TP+FN}
F1=Precision+Recall2⋅Precision⋅Recall=2TP+TP+FN2TP
- AUC(ROC曲线下面积)
AUC的值可以表示为预测模型对于随机选择一个正样本和一个负样本能够给出正确的分类预测的概率大小。因此AUC的值越大,说明模型的分类效果越优秀
ROC曲线以真阳性率为纵坐标,以假阳性率为横坐标绘制的性能评价曲线。
其中真阳性率为
T
P
P
\frac{TP}{P}
PTP
假阳性率为
F
P
N
\frac{FP}{N}
NFP
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EUeiADSa-1685858452101)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230601110704055.png)]](https://img-blog.csdnimg.cn/74ef0da38fbc4d69926bfe66c4ad559b.png)
ROC曲线越靠近左上角,说明其对应模型越可靠。ROC曲线下面的面积(Area Under Curve, AUC)越大,模型越可靠。
- R-squared(R平方)
R方,决定系数,又称拟合优度,通常用来描述数据对模型拟合程度的好坏,表示自变量X对因变量Y的解释程度。R方的取值在[0,1]之间,越接近1,说明回归拟合效果越好。比如R方=0.5,那么说明自变量可以解释因变量50%的变化原因。
R
2
=
1
−
∑
i
=
1
n
(
y
i
−
y
^
i
)
2
∑
i
=
1
n
(
y
i
−
y
ˉ
i
)
2
=
1
−
S
S
E
S
S
T
=
S
S
R
S
S
T
R^2 = 1-\frac{\sum_{i=1}^{n}(y_i-\hat y_i)^2}{\sum_{i=1}^{n}(y_i-\bar y_i)^2} = 1-\frac{SSE}{SST}=\frac{SSR}{SST}
R2=1−∑i=1n(yi−yˉi)2∑i=1n(yi−y^i)2=1−SSTSSE=SSTSSR
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-hF6hryV9-1685858452102)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230601112430309.png)]](https://img-blog.csdnimg.cn/9c73b0cdf12f4ada8a4ac4f0c91c4baa.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-t0j0jC6w-1685858452104)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230601112350131.png)]](https://img-blog.csdnimg.cn/0841b6545e92489282ab35d31ab1b30f.png)
具体内容
针对前面的铺垫内容,我们来开始对线性模型的具体学习,一般我们在实际应用中待检测的物体都有多种属性,根据多个属性值x来确定最终的结果值y。用数学描述如下:

线性回归模型:
f
(
x
)
=
w
1
x
1
+
w
2
x
2
+
.
.
.
+
w
d
x
d
+
b
f(x)=w_1x_1+w_2x_2+...+w_dx_d+b
f(x)=w1x1+w2x2+...+wdxd+b
向量形式:
f
(
x
)
=
w
T
x
+
b
f(x)=w^Tx+b
f(x)=wTx+b
将问题抽象成数学公式后,就转化成了对w、b值进行求解的数学问题,那如何求解出w和b呢?
上一节讲到的损失函数就是重要的解题依据,我们采用均方误差最小化的形式来使f(x)无限逼近真实值,从而确定w和b
首先对于单个属性值的预测结果
f
(
x
i
)
=
w
x
i
+
b
使得
f
(
x
i
)
∽
y
i
f(x_i)=wx_i+b 使得 f(x_i)\backsim y_i
f(xi)=wxi+b使得f(xi)∽yi
使得均方误差最小化:(因为1/m是固定值,不影响最后结果可以省去)
(
w
∗
,
b
∗
)
=
a
r
g
m
i
n
∑
i
=
1
m
(
f
(
x
i
)
−
y
i
)
2
=
a
r
g
m
i
n
∑
i
=
1
m
(
y
i
−
w
x
i
−
b
)
2
=
a
r
g
m
i
n
E
(
w
,
b
)
(w^*,b^*)=argmin\sum_{i=1}^{m}(f(x_i)-y_i)^2=argmin\sum_{i=1}^{m}(y_i-wx_i-b)^2=argminE_{(w,b)}
(w∗,b∗)=argmini=1∑m(f(xi)−yi)2=argmini=1∑m(yi−wxi−b)2=argminE(w,b)
- 应用:最小二乘法:找到一条直线,使得所有样本到直线上的欧式距离之和最小
分别对w、b求导可得
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-isy8O584-1685858452106)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230602182910621.png)]](https://img-blog.csdnimg.cn/a8df1a58f7cd48d9bdc2af70d132f181.png)
∂ E ( w , b ) ∂ w = 2 ( w ∑ i = 1 m x i 2 − ∑ i = 1 m ( y i − b ) x i ) \frac{\partial E_{(w,b)} }{\partial w}=2(w\sum_{i=1}^{m}x_i^2-\sum_{i=1}^{m}(y_i-b)x_i) ∂w∂E(w,b)=2(wi=1∑mxi2−i=1∑m(yi−b)xi)
∂ E ( w , b ) ∂ b = 2 ( m b − ∑ i = 1 m ( y i − w x i ) ) \frac{\partial E_{(w,b)}}{\partial b}=2(mb-\sum_{i=1}^{m}(y_i-wx_i)) ∂b∂E(w,b)=2(mb−i=1∑m(yi−wxi))
令导数值为0得到w、b表达式
多元线性回归
上述我们对单个属性对应的单个w和b进行计算,但是在实际应用中,样本数据中可能会有多个属性,他们共同影响着最终的预测值f(x),因此我们要把一维的情况拓展到多维,得到更一般的表达式:
f
(
x
i
)
=
w
T
x
i
+
b
,
使得
f
(
x
i
)
∽
y
i
f(x_i)=w^Tx_i+b,使得f(x_i)\backsim y_i
f(xi)=wTxi+b,使得f(xi)∽yi
将w和
吸收入向量中:
w
^
=
(
w
1
w
2
⋮
w
d
b
)
=
(
w
b
)
\hat{w}=\left( \begin{matrix} w_{1} \\ w_{2} \\ \vdots \\ w_{d} \\ b \\ \end{matrix} \right) = \left( \begin{matrix} w \\ b \\ \end{matrix} \right)
w^=
w1w2⋮wdb
=(wb)
X = [ x 11 x 12 ⋯ x 1 d 1 x 21 x 22 ⋯ x 2 d 1 ⋮ ⋮ ⋱ ⋮ ⋮ x m 1 x m 2 ⋯ x m d 1 ] = [ x 1 T 1 x 2 T 1 ⋮ ⋮ x m T 1 ] = [ X 1 X 2 ⋮ X m ] X = \left[ \begin{matrix} x_{11} & x_{12} & \cdots & x_{1d} & 1 \\ x_{21} & x_{22} & \cdots & x_{2d} & 1 \\ \vdots & \vdots & \ddots & \vdots & \vdots \\ x_{m1} & x_{m2} & \cdots & x_{md} & 1 \\ \end{matrix} \right] = \left[ \begin{matrix} x_1^T & 1 \\ x_2^T & 1 \\ \vdots & \vdots \\ x_m^T & 1 \\ \end{matrix} \right] = \left[ \begin{matrix} X_1\\ X_2\\ \vdots \\ X_m\\ \end{matrix} \right] X= x11x21⋮xm1x12x22⋮xm2⋯⋯⋱⋯x1dx2d⋮xmd11⋮1 = x1Tx2T⋮xmT11⋮1 = X1X2⋮Xm
所有样本点对应的真实值:
y
=
(
y
1
y
2
⋮
y
m
)
y = \left( \begin{matrix} y_{1} \\ y_{2} \\ \vdots \\ y_{m} \\ \end{matrix} \right)
y=
y1y2⋮ym
对于单个样本的预测值可以如下式子表示:
f
(
x
1
)
=
x
1
T
⋅
w
+
b
=
X
1
⋅
w
^
f(x_1) = x_1^T · w + b = X_1·\hat{w}
f(x1)=x1T⋅w+b=X1⋅w^
所有样本的预测值可以如下式子表示:
f
(
x
)
=
X
w
^
f(x) = X\hat{w}
f(x)=Xw^
因此多元情况下的差值函数也类似于单元,可以利用向量进行运算。
差
值
2
=
(
y
i
−
f
(
x
i
)
)
2
=
(
y
−
X
w
^
)
2
=
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
差值² = (y_i-f(x_i))^2 = (y-X\hat{w})^2=(y-X\hat{w})^T(y-X\hat{w})
差值2=(yi−f(xi))2=(y−Xw^)2=(y−Xw^)T(y−Xw^)
利用最小二乘法来找到合适的w、b值
(
w
∗
,
b
∗
)
=
w
^
∗
=
a
r
g
m
i
n
(
y
−
X
w
^
)
T
(
y
−
X
w
^
)
(w^*,b^*)=\hat{w}^*=argmin(y-X\hat{w})^T(y-X\hat{w})
(w∗,b∗)=w^∗=argmin(y−Xw^)T(y−Xw^)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Wo62c97U-1685858452108)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230602182938877.png)]](https://img-blog.csdnimg.cn/ba9a6f3119fe438fac0c170d161ed194.png)
∂ E w ^ ∂ w ^ = 2 X T ( X w ^ − y ) \frac{\partial E_{\hat{w}}}{\partial \hat{w}} = 2X^T(X\hat{w}-y) ∂w^∂Ew^=2XT(Xw^−y)
w ^ ∗ = ( X T X ) − 1 X T y \hat{w}^* = (X^TX)^{-1}X^Ty w^∗=(XTX)−1XTy
f ( x ^ i ) = X w ^ = x ^ i ( X T X ) − 1 X T y f(\hat{x}_i) = X\hat{w} = \hat{x}_i(X^TX)^{-1}X^Ty f(x^i)=Xw^=x^i(XTX)−1XTy
阅读到这里我们要去思考一个问题,就是对于X^TX这个矩阵,它是否一定可逆呢?
答案是不一定的,因此可能在实际求解中,w有多个值,均可以使差值最小化。
拓展知识:
∂
(
x
T
A
x
)
∂
x
=
A
x
+
A
T
x
,其中
A
是常数矩阵
\frac{\partial (x^T A x)}{\partial x}=Ax+A^Tx,其中A是常数矩阵
∂x∂(xTAx)=Ax+ATx,其中A是常数矩阵
∂ ( x T α ) ∂ x = ∂ ( α T x ) ∂ x = α ,其中 a 为常数向量 \frac{\partial(x^T \alpha)}{\partial x}=\frac{\partial(\alpha^Tx)}{\partial x}=\alpha,其中a为常数向量 ∂x∂(xTα)=∂x∂(αTx)=α,其中a为常数向量
广义线性模型
针对之前学习的线性回归模型思考几个问题:
- x与y之间的变化不是线性的,存在非线性关系还可以像之前那样定义吗?
- 预测数据和真实之间的差值不是常数,且随x变化,如何来界定呢?
- 线性回归假设在因变量正态分布的前提上,导致因变量必须是连续的,若是离散值如何处理呢?
因此在原来线性回归的基础上又衍生出了种类繁多的线性类模型。
在线性回归基础上,在等号的左边或右边加上了一个函数,从而能够让模型更好的捕捉一般规律,此时该模型就被称为广义线性模型,该函数就被称为联系函数。
广义线性模型的提出初衷上还是为了解决非线性相关的预测问题。
y = g − 1 ( w T x + b ) 其中 g ( ⋅ ) 是联系函数 y = g^{-1}(w^Tx+b) 其中g(·)是联系函数 y=g−1(wTx+b)其中g(⋅)是联系函数
实战解析(讲的很好)
逻辑回归模型(对数几率回归)
事先申明,虽然它叫逻辑“回归”,但是它的主要任务是进行二分类。
几率(odd)与对数几率
几率不是概率,而是一个事件发生与不发生的概率的比值。假设某件事发生的概率为p,则该件事不发生的概率为1-p,则该事件的几率:
o
d
d
(
p
)
=
p
1
−
p
odd(p)=\frac{p}{1-p}
odd(p)=1−pp
在几率的基础上取e为底的对数,怎么这件事的对数几率(logit):
l
o
g
i
t
(
p
)
=
l
n
p
1
−
p
logit(p)=ln\frac{p}{1-p}
logit(p)=ln1−pp
对数几率模型
如果我们将对数几率看成是一个函数,并将其作为联系函数,则该广义线性模型为:
g
(
y
)
=
l
n
y
1
−
y
=
w
^
T
⋅
x
^
g(y)=ln\frac{y}{1-y}=\hat w^T·\hat x
g(y)=ln1−yy=w^T⋅x^
可以将其反解出来:
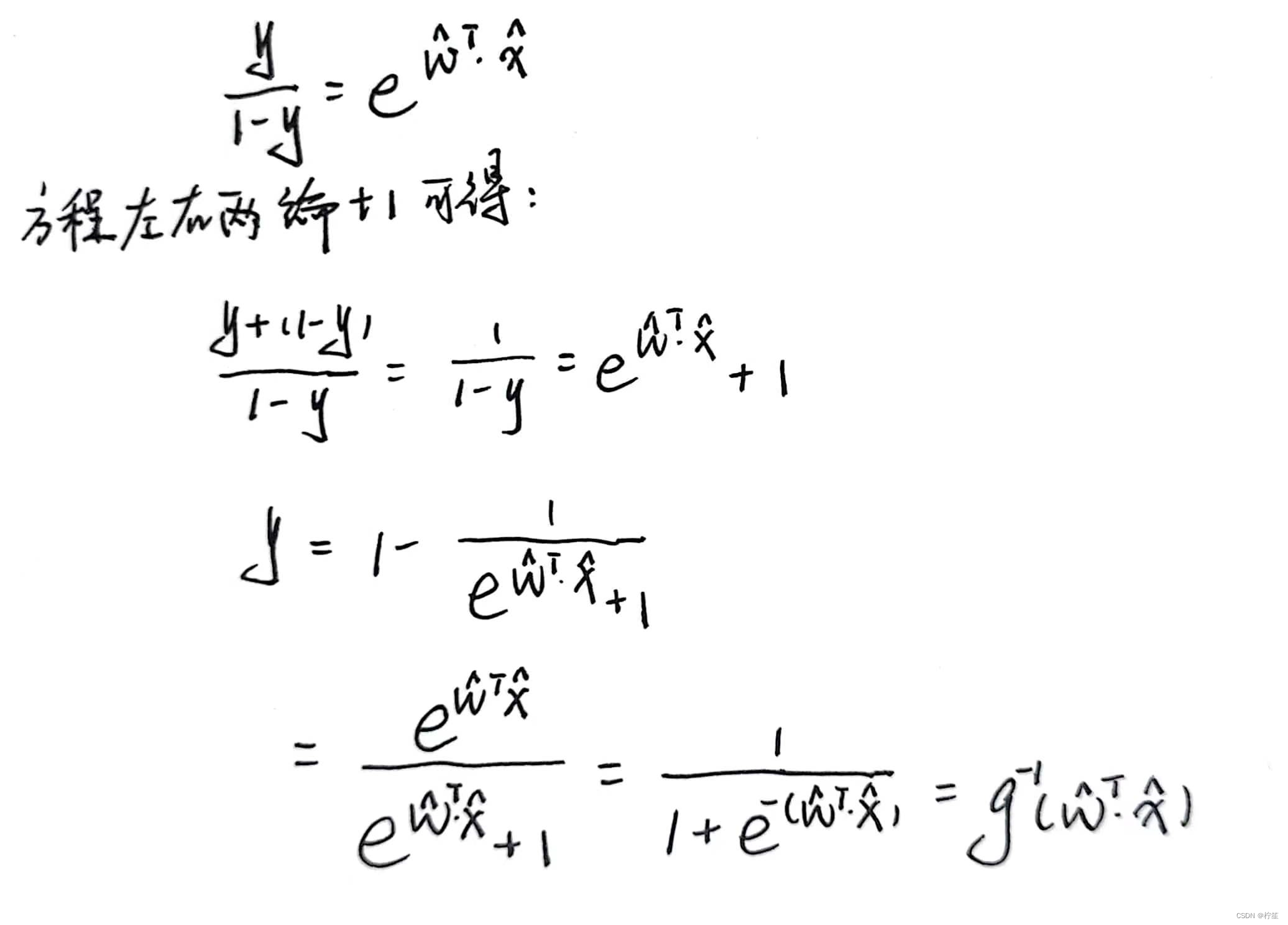
我们将其抽象成数学公式的话,其实可以表示为:
f
(
z
)
=
1
1
+
e
−
z
f(z) =\frac{1}{1+e^{-z}}
f(z)=1+e−z1
那我们将这个图像绘制出来看看它的特性:
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-LblcXVZi-1685858452114)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230603112413160.png)]](https://img-blog.csdnimg.cn/3704af60cf5f4dfdb932ca0524a415a0.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-BPq9iCMi-1685858452116)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230603112455478.png)]](https://img-blog.csdnimg.cn/3c396627d3cb459f945cf1f5c142f279.png)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-IrcjbcRe-1685858452117)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230603225320507.png)]](https://img-blog.csdnimg.cn/f490ce4689154c349e4d57ed96237305.png)
读到这里大家可能会产生疑问:
-
为什么非得探讨对数的情况?指数、绝对值情况不可以吗?
-
为什么最后是sigmoid函数,不可以是其他的函数吗?
拓展了解广义线性回归
数学基础:伯努利分布、极大似然估计、高斯(正态)分布、梯度下降
引入了sigmoid函数,我们可以做什么?
我们假设有一个分类任务,我们要求出正例和反例各自的概率,不妨假设预测函数就是sigmoid函数,具体示例如下:
h
θ
(
x
)
=
g
(
θ
T
x
)
=
1
1
+
e
−
θ
T
x
θ
=
(
w
;
b
)
h_{\theta}(x)=g({\theta}^Tx)=\frac{1}{1+e^{{-\theta}^Tx}} \\ \theta = (w;b)
hθ(x)=g(θTx)=1+e−θTx1θ=(w;b)
正例: P ( y = 1 ∣ x ; θ ) = h θ ( x ) 反例: P ( y = 0 ∣ x ; θ ) = 1 − h θ ( x ) 整合: P ( y ∣ x ; θ ) = ( h θ ( x ) ) y ( 1 − h θ ( x ) ) 1 − y 二分类任务 y 只取 0 , 1 正例:P(y=1|x;\theta)=h_{\theta}(x) \\ 反例:P(y=0|x;\theta)=1-h_{\theta}(x) \\ 整合:P(y|x;\theta)=(h_{\theta}(x))^y(1-h_{\theta}(x))^{1-y}\\ 二分类任务y只取0,1 正例:P(y=1∣x;θ)=hθ(x)反例:P(y=0∣x;θ)=1−hθ(x)整合:P(y∣x;θ)=(hθ(x))y(1−hθ(x))1−y二分类任务y只取0,1
似然函数:
L
(
θ
)
=
∏
i
=
1
m
P
(
y
i
∣
x
i
;
θ
)
=
∏
i
=
1
m
(
h
θ
(
x
i
)
)
y
i
(
1
−
h
θ
(
x
i
)
)
1
−
y
i
L(\theta)=\prod_{i=1}^mP(y_i|x_i;\theta) =\prod_{i=1}^m(h_{\theta}(x_i))^{y_i}(1-h_{\theta}(x_i))^{1-y_i}
L(θ)=i=1∏mP(yi∣xi;θ)=i=1∏m(hθ(xi))yi(1−hθ(xi))1−yi
概率的连乘会使最后数据过小无法有效计算,想办法消去连乘,便引进了对数似然函数:
l
(
θ
)
=
l
o
g
L
(
θ
)
=
∑
i
=
1
m
(
y
i
l
o
g
h
θ
(
x
i
)
+
(
1
−
y
i
)
l
o
g
(
1
−
h
θ
(
x
i
)
)
)
l(\theta)=logL(\theta)=\sum_{i=1}^{m}(y_ilogh_\theta(x_i)+(1-y_i)log(1-h_\theta(x_i)))
l(θ)=logL(θ)=i=1∑m(yiloghθ(xi)+(1−yi)log(1−hθ(xi)))
此时要求对数似然函数的最大值:但是求最大是一个梯度上升的问题,我们平常所熟悉的是梯度下降的问题,那就要进行问题的转化。
J
(
θ
)
=
−
1
m
l
(
θ
)
J(\theta)=- \frac{1}{m}l(\theta)
J(θ)=−m1l(θ)
利用梯度下降方法求出迭代方向(即导数值)
![[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-DlulRH3J-1685858452118)(C:\Users\liyi0\AppData\Roaming\Typora\typora-user-images\image-20230603225351181.png)]](https://img-blog.csdnimg.cn/13f904139a6a4a53bfa135a503599fd2.png)
x
i
j
表示第
i
个样本的第
j
个特征
x_i^j 表示第i个样本的第j个特征
xij表示第i个样本的第j个特征
参数更新:
θ
j
:
=
θ
j
−
α
1
m
∑
i
=
1
m
(
h
θ
(
x
i
)
−
y
i
)
x
i
j
\theta_j :=\theta_j-\alpha\frac{1}{m}\sum_{i=1}^{m}(h_\theta(x_i)-y_i)x_i^j
θj:=θj−αm1i=1∑m(hθ(xi)−yi)xij
这个式子中的α表示更新的步长(学习率),后面表示方向。方向乘以步长表示我要更新的内容
拓展:多分类的softmax
类别不平衡问题
什么时候需要去处理类别不平衡的问题:在这里插入图片描述
当一个样本中的“小类”比样本中的“大类”更为重要时才需要对类别不平衡进行处理。在这里插入图片描述


推荐讲解:周志华老师西瓜书
本文为机器学习入门篇,暂时不对复杂问题进行探讨。对于中间提到的公式最好是手动推导!