算法原理

t-SNE 的基本思想是将高维数据映射到低维空间，同时保留数据间的局部结构。具体而言，给定一个高维数据集 X = { x 1 , … , x n } \mathbf{X}=\{\mathbf{x}_1,\dots,\mathbf{x}_n\} X={x1​,…,xn​}，其中 ${\mathbf{x}}_i\in {\mathbb{R}}^D$，要将其映射到一个 $d$ 维的空间 Y = { y 1 , … , y n } \mathbf{Y}=\{\mathbf{y}_1,\dots,\mathbf{y}_n\} Y={y1​,…,yn​}，其中 ${\mathbf{y}}_i\in {\mathbb{R}}^d$，且 $d\ll D$。

与其他降维算法不同的是，t-SNE 旨在保持数据点之间的局部相似性，即将高维空间中距离接近的点映射到低维空间中距离仍然较近的位置。为了实现这个目标，t-SNE 建立了一个概率模型，用于将数据点从高维空间映射到低维空间。具体地，它假设在高维空间中距离接近的点在低维空间中也有更大的概率被选择为临近点。

在 t-SNE 中，每个高维数据点 ${\mathbf{x}}_i$ 对应一个在低维空间中的概率分布 $q_i$，用于描述 ${\mathbf{x}}_i$ 在低维空间中的位置。与此同时，为了保留其局部结构，还需要为每个 ${\mathbf{x}}_i$ 建立一个概率分布 $p_i$，用于描述 ${\mathbf{x}}_i$ 与其它数据点之间的相似性。在 t-SNE 中，用采用的是高斯分布，即

$$p_{i,j}=\frac{p({\mathbf{x}}_i|{\mathbf{x}}_j)}{{\sum }_{k\ne i}p({\mathbf{x}}_i|{\mathbf{x}}_k)},$$

其中 $p({\mathbf{x}}_i|{\mathbf{x}}_j)$ 表示在高维空间中，${\mathbf{x}}_i$ 在以 ${\mathbf{x}}_j$ 为中心的局部高斯分布中出现的概率密度。它的定义为：

$$p({\mathbf{x}}_i|{\mathbf{x}}_j)=\frac{\exp (-\Vert {\mathbf{x}}_i-{\mathbf{x}}_j{\Vert }^2/(2{\sigma }_j^2))}{{\sum }_{k\ne j}\exp (-\Vert {\mathbf{x}}_i-{\mathbf{x}}_k{\Vert }^2/(2{\sigma }_j^2))}$$

其中 ${\sigma }_j$ 是一个尺度参数，用于控制局部邻域的大小。

同样地，我们也需要定义一个低维空间中的概率分布 $q_{i,j}$。在 t-SNE 中，这个概率分布是由一个类似于 softmax 的归一化因子给出的，形式为：

$$q_{i,j}=\frac{(1+\Vert {\mathbf{y}}_i-{\mathbf{y}}_j{\Vert }^2{)}^{-1}}{{\sum }_{k\ne l}(1+\Vert {\mathbf{y}}_k-{\mathbf{y}}_l{\Vert }^2{)}^{-1}}$$

其中 $(1+\Vert {\mathbf{y}}_i-{\mathbf{y}}_j{\Vert }^2{)}^{-1}$ 可以解释成一个 t-分布。

t-SNE 的目标函数定义为两个概率分布之间的 KL 散度，即

$$\mathrm{KL}(P||Q)=\sum _i\sum _j{p}_{i,j}\log \frac{p_{i,j}}{q_{i,j}}$$

为了最小化 KL 散度，可以采用梯度下降法来求解。因为 KL 散度没有解析解，所以梯度需要通过自动微分或其他数值方法进行计算。

t-SNE 的基本思想是在高维数据空间和低维嵌入空间中分别构建高斯分布和 t-分布，在两个空间中寻找相同的邻居，并最小化两个概率分布之间的差异。

示例一

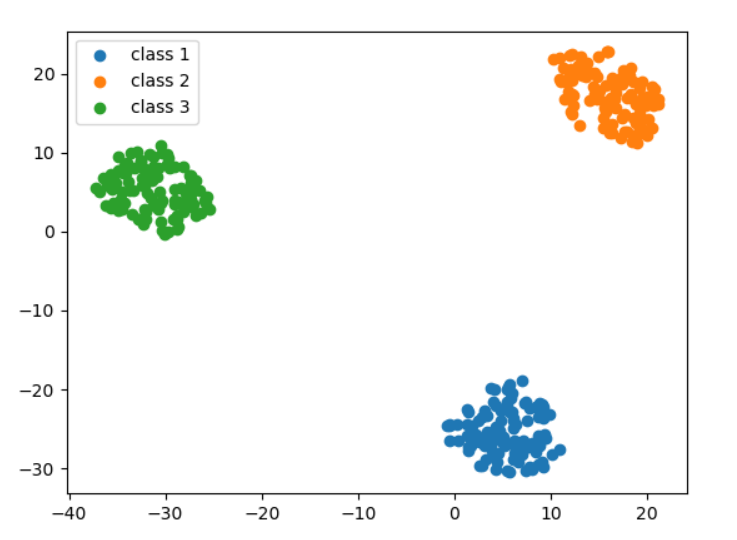
生成一批符合高斯分布的高维样本，把它们降到二维来可视化。这些高斯分布的样本符合以下三个特征：

1. 所有的数据点分别属于三个类别，
2. 每一个样本点是三维的，
3. 第一类样本均值为(0,0,0), 第二类均值为(1,1,0),第三类均值为(-1,1,1)

from sklearn.datasets import make_blobs
from sklearn.manifold import TSNE
import matplotlib.pyplot as plt
import numpy as np

# 生成三个高斯分布，每个高斯分布包含100个样本点
X, y = make_blobs(n_samples=300, centers=[[0, 0, 0], [1, 1, 0], [-1, 1, 1]], cluster_std=0.2)

# 初始化 t-SNE 模型，设置降维后的维度为 2 维
tsne = TSNE(n_components=2)

# 对数据进行降维
X_tsne = tsne.fit_transform(X)

# 将三个类别的数据点分别提取出来
class_1 = X_tsne[y == 0]
class_2 = X_tsne[y == 1]
class_3 = X_tsne[y == 2]

# 可视化结果
plt.scatter(class_1[:, 0], class_1[:, 1], label='class 1')
plt.scatter(class_2[:, 0], class_2[:, 1], label='class 2')
plt.scatter(class_3[:, 0], class_3[:, 1], label='class 3')
plt.legend()
plt.show()

示例二

把MINIST直接展开可视化

from sklearn.manifold import TSNE
from sklearn.datasets import fetch_openml
import matplotlib.pyplot as plt

# 获取 MNIST 数据集
mnist = fetch_openml('mnist_784')

# 取前1000张图片和对应的标签作为数据进行处理
X = mnist.data[:1000]
y = mnist.target[:1000]

# 初始化 t-SNE 模型，设置降维后的维度为 2 维
tsne = TSNE(n_components=2)

# 对数据进行降维
X_tsne = tsne.fit_transform(X)

# 绘制结果
plt.figure(figsize=(10, 10))
plt.scatter(X_tsne[:, 0], X_tsne[:, 1], c=y.astype(int), cmap='jet')
plt.colorbar()
plt.show()

参考资料：

[1] van der Maaten, L.J.P., Postma, E.O. and van den Herik, H.J., 2009. Dimensionality reduction: A comparative review. Journal of Machine Learning Research, 10, pp.66-71.

[2] Maaten, L.v.d. and Hinton, G., 2008. Visualizing data using t-SNE. Journal of machine learning research, 9(Nov), pp.2579-2605.
[3]https://distill.pub/2016/misread-tsne
[4]https://scikit-learn.org/stable/auto_examples/manifold/plot_t_sne_perplexity.html