动态规划

动态规划思维（基础）

状态表示（最重要）

状态转移方程（最难）

初始化（细节）

填表顺序（细节）

返回值（结果）

解码方法⭐⭐

【题目解析】

【算法原理】

C++ 算法代码

复杂度分析

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

【DP边界、初始化技巧】

C++ 算法代码

【空间优化 - 滚动数组】

C++ 算法代码

不同路径⭐⭐

【题目解析】

【算法原理】

C++ 算法代码

复杂度分析

【DP边界、初始化】

C++ 算法代码

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

不同路径Ⅱ⭐⭐

【算法原理】

C++ 算法代码

复杂度分析

【DP边界、初始化】

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

礼物的最大价值⭐⭐

【算法原理】

C++ 算法代码

复杂度分析

【DP边界、初始化】

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

下降路径最小和⭐⭐

【算法原理】

C++ 算法代码

复杂度分析

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

最小路径和⭐⭐

【算法原理】

C++ 算法代码

复杂度分析

【DP边界、初始化】

【空间优化 - 滚动数组】

C++ 算法代码

复杂度分析

动态规划

动态规划思维（基础）

动态规划一般会先定义一个dp表，dp表一般为一维数组 / 二位数组。如：一维数组，会先创建一个一维数组（dp表），接下来就是想办法将这个dp填满，而填满之后里面的某一个值就是最终结果。

状态表示（最重要）

#问：是什么？

就是dp[i]所代表的含义。

#问：怎么来？

题目要求。
经验 + 题目要求。
分析问题的过程中，发现重复子问题。

状态转移方程（最难）

#问：是什么？

dp[i] = ?。

初始化（细节）

#问：有什么作用？

保证填表的时候不越界。

dp表是根据状态转移方程进行的，而状态转移方程是通过已有状态推出未知状态。

填表顺序（细节）

#问：有什么作用？

为了填写当前状态的时候，所需要的状态已经计算过了。

返回值（结果）

题目要求 + 状态表示。

解码方法⭐⭐

91. 解码方法 - 力扣（LeetCode）

【题目解析】

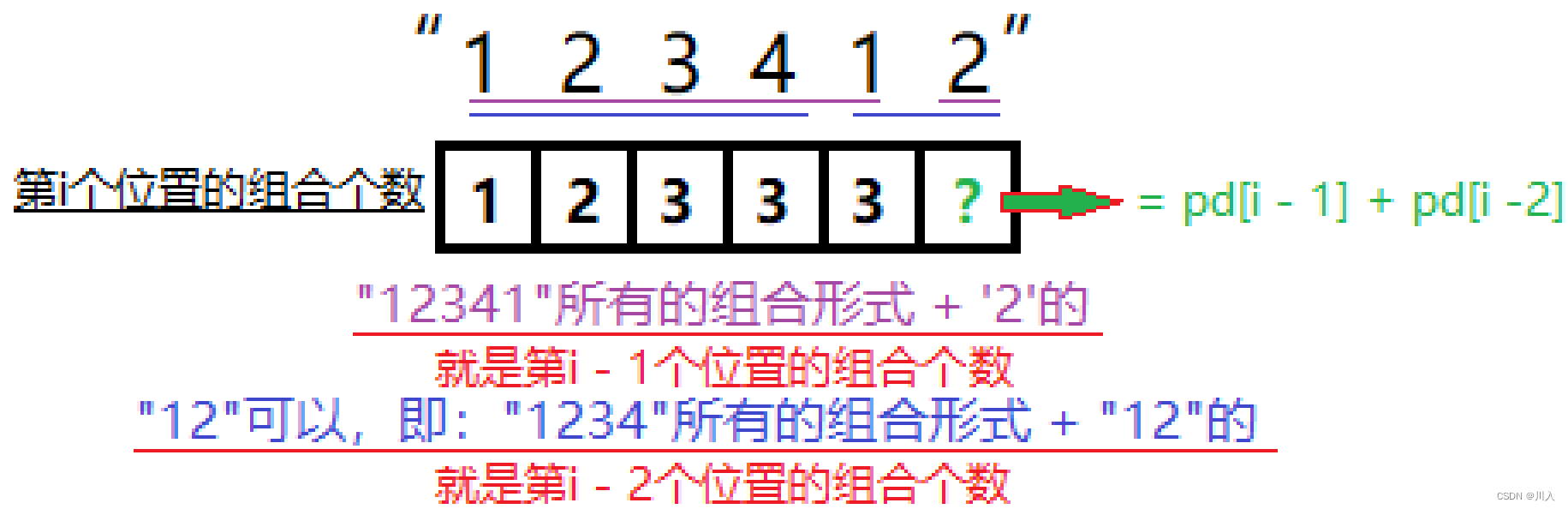
dp[i] 表示：字符串中 [0，i] 区间上，⼀共有多少种编码方法。

【算法原理】

#：状态表示：

根据以往的经验，对于大多数线性 dp ，我们经验上都是「以某个位置结束或者开始」做⽂章，这里我们继续尝试「用 i 位置为结尾」结合「题目要求」来定义状态表示。dp[i] 表示：字符串中 [0 ， i] 区间上，⼀共有多少种编码方法。

#：状态转移方程：

定义好状态表示，我们就可以分析 i 位置的 dp 值，如何由「前面」或者「后面」的信息推导出来。关于 i 位置的编码状况，我们可以分为下⾯两种情况：

让 i 位置上的数单独解码成一个字母，成功：dp[i] += dp[i - 1]，失败：dp[i] += 0
让 i 位置上的数与 i - 1 位置上的数结合，解码成一个字母，成功：dp[i] += dp[i - 2]，失败：dp[i] += 0

#：初始化：

从我们的递推公式可以看出， dp[i] 在 i = 0 以及 i = 1 的时候是没有办法进行推导的，因为 dp[-2] 或 dp[-1] 不是⼀个有效的数据。因此我们需要在填表之前，将 0, 1 位置的值初始化。

#：填表顺序：

毫⽆疑问是「从左往右」。

#：返回值：

应该返回 dp[n - 1] 的值，表示在 [0, n - 1] 区间上的编码方法。

C++ 算法代码

使用⼀维数组：

class Solution {
public:
    int numDecodings(string s) {
        // 处理边界情况
        if(s[0] == '0' || s.empty()) return 0;
        if(s.size() == 1) return 1;

        // 1、创建dp表
        vector<int> dp(s.size(), 0);

        // 2、初始化
        dp[0] = 1;
        if(s[1] == '0' && s.substr(0, 2) > "26") dp[1] = 0;
        else if(s[1] == '0' && s.substr(0, 2) <= "26") dp[1] = 1;
        else if(s.substr(0, 2) > "26") dp[1] = 1;
        else dp[1] = 2;


        // 3、填表
        for(int i = 2; i < s.size(); i++)
        {
            if(s[i] != '0')
                dp[i] += dp[i - 1];
            
            // 计算两位组成是否合格
            if(s[i - 1] != '0' && s.substr(i - 1, 2) <= "26")
                dp[i] += dp[i - 2];
        }

        // 4、返回值
        return dp[s.size() - 1];
    }
};

复杂度分析

时间复杂度：O(n)，一层for循环。
空间复杂度：O(n)。

【空间优化 - 滚动数组】

通过上述图可以发现。

dp[i]是只与前两个元素相关，所以我们可以将代码写为如下：

C++ 算法代码

class Solution {
public:
    int numDecodings(string s) {
        // 处理边界情况
        if(s[0] == '0' || s.empty()) return 0;
        if(s.size() == 1) return 1;

        // 1、创建dp表
        vector<int> dp(2, 0);

        // 2、初始化
        dp[0] = 1;
        if(s[1] == '0' && s.substr(0, 2) > "26") dp[1] = 0;
        else if(s[1] == '0' && s.substr(0, 2) <= "26") dp[1] = 1;
        else if(s.substr(0, 2) > "26") dp[1] = 1;
        else dp[1] = 2;

        // 3、填表
        for(int i = 2; i < s.size(); i++)
        {
            int tmp = 0;
            if(s[i] != '0')
                tmp += dp[1];
            
            // 计算两位组成是否合格
            if(s[i - 1] != '0' && s.substr(i - 1, 2) <= "26")
                tmp += dp[0];
            dp[0] = dp[1], dp[1] = tmp;
        }

        // 4、返回值
        return dp[1];
    }
};

复杂度分析

时间复杂度：O(n)，一层for循环。
空间复杂度：O(1)。

【DP边界、初始化技巧】

在上述的代码中可以发现，代码的初始化写的好长，并且尤其是对于dp[1]的初始化和后续的dp[i]填表的相似度非常的高。那岂不是将初始化dp[1]部分放到填表的环节里更好！

也就是在DP中经常会出现处理，边界复杂、繁琐的情况，而为了能更好的处理这种类似的情况，是由一个技巧的：就是将整个dp表统一向后移动一位，也就是多开一个位置。

虚拟位置的作用。

越过令人讨厌的dp[1]，让其在填表里面去搞定。这个看似是很舒服的，但是我们需要注意两个注意事项：

虚拟节点里面的值，要保证后面的填表的值是正确的。
下标的映射关系。

分析上述，根据填表的规则，并且由于原dp[1]变为现在的dp[2]，所以是dp[2] = dp[0] + dp[1]。而dp[1]完完全全就是我们初始化的，所以不会出错，于是就看dp[0]。而dp[0]是我们进行虚拟出来的，于是其的值是至关重要的。

一般情况下新增的虚拟位置都是0，但是此处不一样。此处如果dp[1] + dp[2]位置的值符合解码为字母，那么就需要加上dp[0]的值，所以证明是找到了一种解码方式，那么就是1，于是dp[0] = 1。

C++ 算法代码

class Solution {
public:
    int numDecodings(string s) {
        // 处理边界情况
        if(s[0] == '0' || s.empty()) return 0;
        if(s.size() == 1) return 1;

        // 1、创建dp表
        vector<int> dp(s.size() + 1, 0);

        // 2、初始化
        dp[0] = 1, dp[1] = 1;

        // 3、填表
        for(int i = 1; i < s.size(); i++)
        {
            if(s[i] != '0')
                dp[i + 1] += dp[i];
            
            // 计算两位组成是否合格
            if(s[i - 1] != '0' && s.substr(i - 1, 2) <= "26")
                dp[i + 1] += dp[i - 1];
        }

        // 4、返回值
        return dp[s.size()];
    }
};

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int numDecodings(string s) {
        if(s[0] == '0' || s.empty()) return 0;
        if(s.size() == 1) return 1;

        // 1、创建dp表
        vector<int> dp(2, 0);

        // 2、初始化
        dp[0] = 1, dp[1] = 1;

        // 3、填表
        for(int i = 1; i < s.size(); i++)
        {
            int tmp = 0;
            if(s[i] != '0')
                tmp += dp[1];
            
            // 计算两位组成是否合格
            if(s[i - 1] != '0' && s.substr(i - 1, 2) <= "26")
                tmp += dp[0];
            dp[0] = dp[1], dp[1] = tmp;
        }

        // 4、返回值
        return dp[1];
    }
};

不同路径⭐⭐

62. 不同路径 - 力扣（LeetCode）

【题目解析】

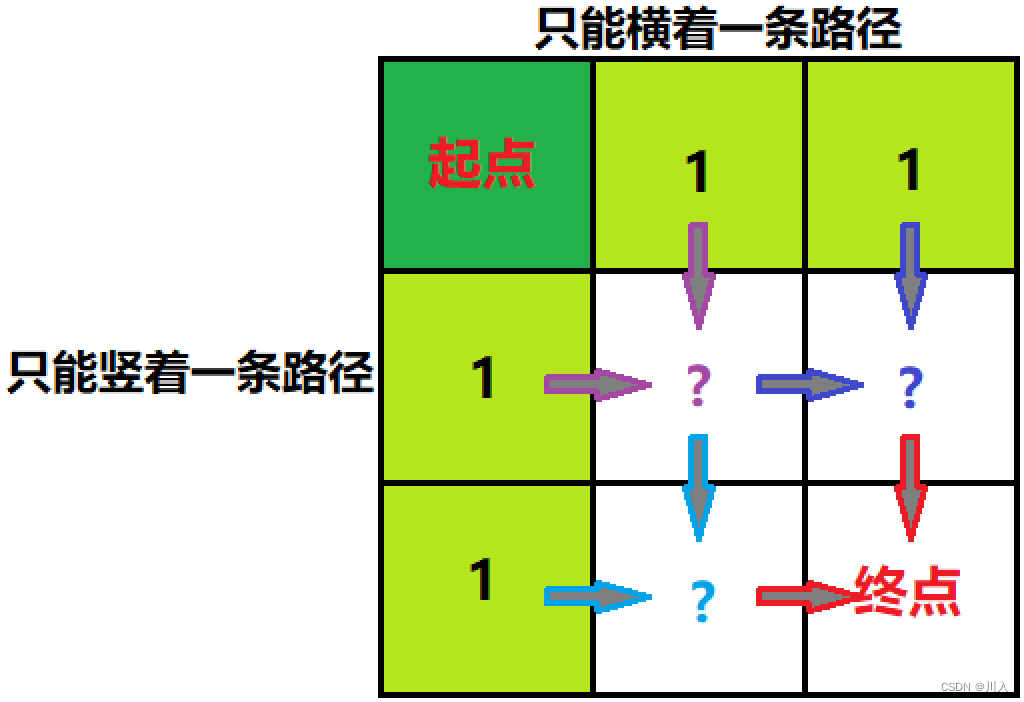
dp[i][j]表示：到达 [i, j] 位置的路径个数。

【算法原理】

#：状态表示：

对于这种「路径类」的问题，我们的状态表示⼀般有两种形式：

从 [i, j] 位置出发，……；
从起始位置出发，到达 [i, j] 位置，……。

这里选择第二种定义状态表示的方式： dp[ i ][ j ] 表示：走到 [ i, j ] 位置处，⼀共有多少种方式。

#：状态转移方程：

如果 dp[ i ][ j ] 表示到达 [ i, j ] 位置的方法数，那么到达 [ i, j ] 位置之前的⼀小步，有两种情况：

从 [ i, j ] 位置的上方（ [ i - 1, j ] 的位置）向下走⼀步，转移到 [ i, j ] 位置
从 [ i, j ] 位置的左方（ [ i, j - 1 ] 的位置）向右走⼀步，转移到 [ i, j ] 位置

由于我们要求的是有多少种方法，因此状态转移方程就呼之欲出了： dp[ i ][ j ] = dp[ i - 1 ][ j ] + dp[ i ][ j - 1 ]。

#：初始化：

对第一行，第一列继续初始化，由于 dp[ 0 ][ j ] 只能由前所来，dp[ i ][ 0 ] 只能由上所来。

#：填表顺序：

根据「状态转移方程」的推导来看，填表的顺序就是「从上往下」填每⼀行，在填写每⼀行的时候「从左往右」。

#：返回值：

根据「状态表示」，我们要返回 dp[m - 1][n - 1] 的值。

C++ 算法代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 处理边界情况
        if(m == 1 && n == 1) return 1;

        // 1、创建dp表
        vector<vector<int>> dp(m, vector(n, 0));

        // 2、初始化
        for(auto& v : dp[0]) v = 1;
        for(int i = 0; i < m; i++) dp[i][0] = 1;

        // 3、填表
        for(int i = 1; i < m; i++)
        {
            for(int j = 1; j < n; j++)
            {
                dp[i][j] += dp[i][j - 1] + dp[i - 1][j];
            }
        }
        
        // 4、返回值
        return dp[m -1][n - 1];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n*m)。

【DP边界、初始化】

可以在最前⾯加上⼀个「辅助结点」，帮助我们初始化。使用这种技巧要注意两个点：

辅助结点里面的值要「保证后续填表是正确的」。
「下标的映射关系」。

在上述的代码中可以发现，代码的初始化需要写两个for循环，无疑也是麻烦的，所以采用DP边界、初始化技巧无疑是很好的。通过上述分析可以发现，由于第一行与第一列，在状态转移方程中 [i - 1]、[j - 1]的越界而导致无法进入填表环节 —— 所以采取多一行，多一列。

将上述的两个for循环初始化值引入：

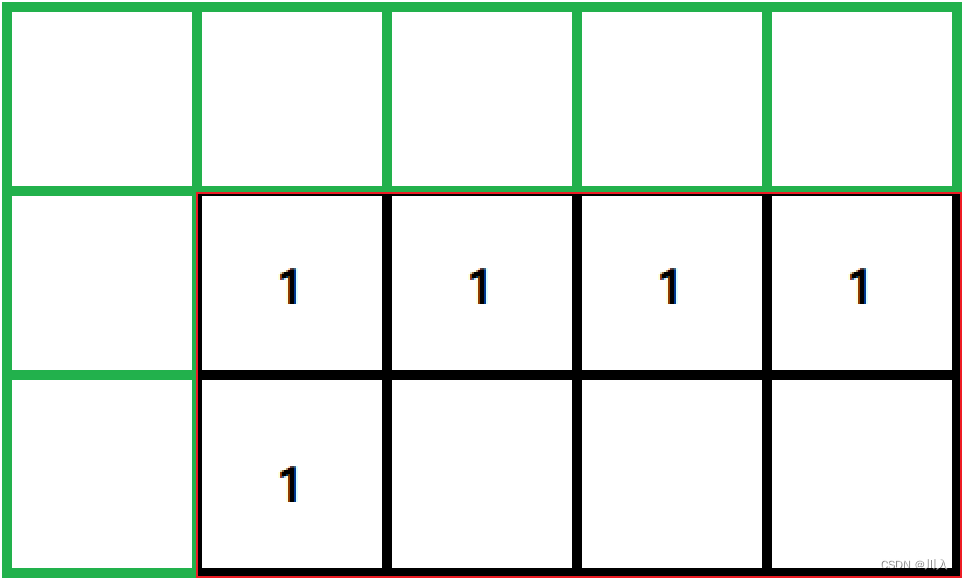
而这个初始化的原因就是第一行只能从左往右，第一列只能从上往下 —— 所以重点是有效范围内的第一个元素为1。

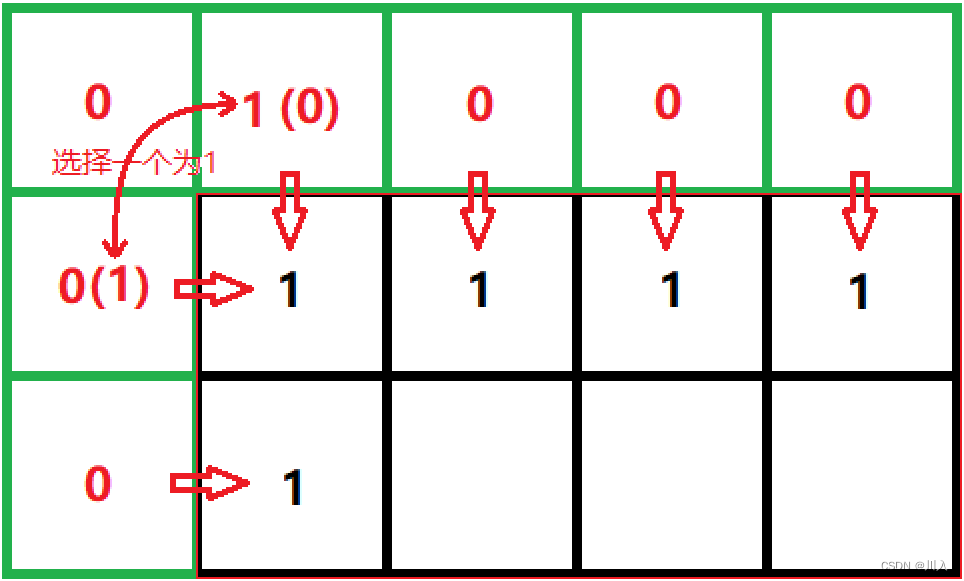
在本题中，添加一行，并且添加⼀列后，只需将 dp[1][0] 的位置初始化为 1 或将 dp[0][1] 的位置初始化为 1 即可。

C++ 算法代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 处理边界情况
        if(m == 1 && n == 1) return 1;

        // 1、创建dp表
        vector<vector<int>> dp(m + 1, vector(n + 1, 0));

        // 2、初始化
        dp[0][1] = 1;
        // dp[1][0] = 1;

        // 3、填表
        for(int i = 1; i < m + 1; i++)
        {
            for(int j = 1; j < n + 1; j++)
            {
                dp[i][j] += dp[i][j - 1] + dp[i - 1][j];
            }
        }
        // 4、返回值
        return dp[m][n];
    }
};

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int uniquePaths(int m, int n) {
        // 处理边界情况
        if(m == 1 && n == 1) return 1;

        // 1、创建dp表
        vector<int> dp(n + 1, 0);

        // 2、初始化
        dp[1] = 1;

        // 3、填表
        for(int i = 1; i < m + 1; i++)
        {
            for(int j = 0; j < n + 1; j++)
            {
                if(j != 0)
                {
                    dp[j] += dp[j - 1];
                }
            }
        }
        
        // 4、返回值
        return dp[n];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n)。

不同路径Ⅱ⭐⭐

63. 不同路径 II - 力扣（LeetCode）

【算法原理】

#：状态表示：

对于这种「路径类」的问题，我们的状态表示⼀般有两种形式：

从 [i, j] 位置出发，……；
从起始位置出发，到达 [i, j] 位置，……。

这里选择第二种定义状态表示的方式： dp[ i ][ j ] 表示：走到 [ i, j ] 位置处，⼀共有多少种方式。

#：状态转移方程：

如果 dp[ i ][ j ] 表示到达 [ i, j ] 位置的方法数，那么到达 [ i, j ] 位置之前的⼀小步，有两种情况：

从 [ i, j ] 位置的上方（ [ i - 1, j ] 的位置）向下走⼀步，转移到 [ i, j ] 位置
从 [ i, j ] 位置的左方（ [ i, j - 1 ] 的位置）向右走⼀步，转移到 [ i, j ] 位置

但是， [i - 1, j] 与 [i, j - 1] 位置都是可能有障碍的，此时从上⾯或者左边是不可能到达 [i, j] 位置的，也就是说，此时的方法数应该是 0。

由此我们可以得出⼀个结论，只要这个位置上「有障碍物」，那么我们就不需要计算这个位置上的值，直接让它等于 0 即可。

#：初始化：

对第一行，第一列继续初始化，由于 dp[ 0 ][ j ] 只能由前所来，dp[ i ][ 0 ] 只能由上所来，并且需要注意的是小心一行 / 一列中出现阻碍，如果有阻碍就会将为唯一的路线卡死。

#：填表顺序：

根据「状态转移方程」的推导来看，填表的顺序就是「从上往下」填每⼀行，在填写每⼀行的时候「从左往右」。

#：返回值：

根据「状态表示」，我们要返回 dp[m - 1][n - 1] 的值。

C++ 算法代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int row = obstacleGrid.size();
        int col = obstacleGrid[0].size();

        // 处理边界情况
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 0) return 1;
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 1) return 0;

        // 1、创建dp表
        vector<vector<int>> dp(row, vector<int>(col, 0));

        // 2、初始化
        int flag = 1;
        for(int i = 0; i<row; i++)
        {
            if(obstacleGrid[i][0] == 1) flag = 0;
            dp[i][0] = flag;
        }
        flag = 1;
        for(int i = 0; i<col; i++)
        {
            if(obstacleGrid[0][i] == 1) flag = 0;
            dp[0][i] = flag;
        }

        // 3、填表
        for(int i = 1; i<row; i++)
        {
            for(int j = 1; j<col; j++)
            {
                if(obstacleGrid[i][j] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        // 4、返回值
        return dp[row - 1][col - 1];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n*m)。

【DP边界、初始化】

与上一题类似的思想。

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int row = obstacleGrid.size();
        int col = obstacleGrid[0].size();

        // 处理边界情况
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 0) return 1;
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 1) return 0;

        // 1、创建dp表
        vector<vector<int>> dp(row + 1, vector<int>(col + 1, 0));

        // 2、初始化
        dp[0][1] = 1;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
        {
            for(int j = 1; j < col + 1; j++)
            {
                if(obstacleGrid[i - 1][j - 1] == 1) continue;
                dp[i][j] = dp[i - 1][j] + dp[i][j - 1];
            }
        }

        // 4、返回值
        return dp[row][col];
    }
};

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
        int row = obstacleGrid.size();
        int col = obstacleGrid[0].size();

        // 处理边界情况
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 0) return 1;
        if(row == 1 && col == 1 && obstacleGrid[0][0] == 1) return 0;

        // 1、创建dp表
        vector<int> dp(col + 1, 0);

        // 2、初始化
        dp[1] = 1;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
        {
            for(int j = 1; j < col + 1; j++)
            {
                if(obstacleGrid[i - 1][j - 1] == 1) 
                    dp[j] = 0;
                else
                    if(j != 0)
                        dp[j] = dp[j - 1] + dp[j];
            }
        }

        // 4、返回值
        return dp[col];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n)。

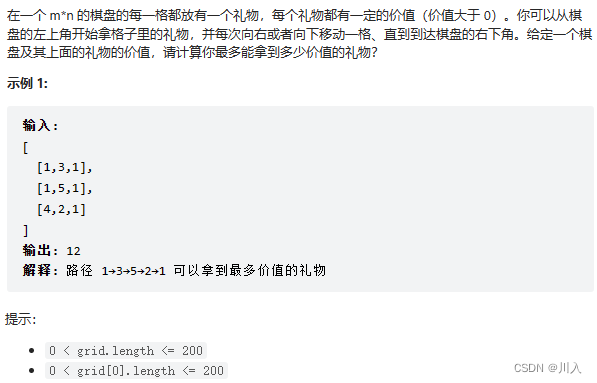
礼物的最大价值⭐⭐

剑指 Offer 47. 礼物的最大价值 - 力扣（LeetCode）

【算法原理】

#：状态表示：

对于这种「路径类」的问题，我们的状态表示⼀般有两种形式：

从 [i, j] 位置出发，……；
从起始位置出发，到达 [i, j] 位置，……。

这里选择第二种定义状态表示的方式： dp[ i ][ j ] 表示：走到 [ i, j ] 位置处，此时的最大价值。

#：状态转移方程：

如果 dp[ i ][ j ] 表示到达 [ i, j ] 位置的方法数，那么到达 [ i, j ] 位置之前的⼀小步，有两种情况：

从 [ i, j ] 位置的上方（ [ i - 1, j ] 的位置）向下走一步，此时到达 [i, j] 位置能拿到的礼物价值为 dp[ i - 1 ][ j ] + grid[ i ][ j ]
从 [ i, j ] 位置的左方（ [ i, j - 1 ] 的位置）向右走一步，此时到达 [i, j] 位置能拿到的礼物价值为 dp[ i ][ j - 1 ] + grid[ i ][ j ]

我们要的是最大值，因此 状态转移方程为：dp[ i ][ j ] = max(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + grid[ i ][ j ] 。

#：初始化：

对第一行，第一列继续初始化，由于 dp[ 0 ][ j ] 只能由前所来，dp[ i ][ 0 ] 只能由上所来。

#：填表顺序：

根据「状态转移方程」的推导来看，填表的顺序就是「从上往下」填每⼀行，在填写每⼀行的时候「从左往右」。

#：返回值：

根据「状态表示」，我们要返回 dp[m - 1][n - 1] 的值。

C++ 算法代码

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(row, vector<int>(col, 0));
        
        // 2、初始化
        dp[0][0] = grid[0][0];
        for(int i = 1; i<col; i++)
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        
        for(int i = 1; i<row; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];

        // 3、填表
        for(int i = 1; i<row; i++)
            for(int j = 1; j<col; j++)
                dp[i][j] = grid[i][j] + max(dp[i - 1][j], dp[i][j - 1]);

        // 4、返回值
        return dp[row - 1][col - 1];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n*m)。

【DP边界、初始化】

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(row + 1, vector<int>(col + 1, 0));
        
        // 2、初始化 - 就是0，创建时已初始化

        // 3、填表
        for(int i = 1; i < row + 1; i++)
            for(int j = 1; j < col + 1; j++)
                dp[i][j] = grid[i - 1][j - 1] + max(dp[i - 1][j], dp[i][j - 1]);

        // 4、返回值
        return dp[row][col];
    }
};

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int maxValue(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<int> dp(col + 1, 0);
        
        // 2、初始化 - 就是0，创建时已初始化

        // 3、填表
        for(int i = 1; i < row + 1; i++)
        {
            for(int j = 1; j < col + 1; j++)
            {
                dp[j] = grid[i - 1][j - 1] + max(dp[j], dp[j - 1]);  
            }
        }

        // 4、返回值
        return dp[col];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n)。

下降路径最小和⭐⭐

931. 下降路径最小和 - 力扣（LeetCode）

【算法原理】

#：状态表示：

对于这种「路径类」的问题，我们的状态表示⼀般有两种形式：

从 [i, j] 位置出发，……；
从起始位置出发，到达 [i, j] 位置，……。

这里选择第二种定义状态表示的方式： dp[ i ][ j ] 表示：走到 [ i, j ] 位置处，所有下降路径中的最小和。

#：状态转移方程：

对于普遍位置 [i, j] ，根据题意得，到达 [i, j] 位置可能有三种情况：

从正上方 [i - 1, j] 位置转移到 [i, j] 位置。
从左上方 [i - 1, j - 1] 位置转移到 [i, j] 位置。
从右上⽅ [i - 1, j + 1] 位置转移到 [i, j] 位置。

我们要的是三种情况下的「最小值」，然后再加上矩阵在 [i, j] 位置的值，于是 状态转移方程为：dp[i][j] = min(dp[i - 1][ j ], min(dp[i - 1][j - 1], dp[i - 1][j + 1])) + matrix[ i ][ j ] 。

#：初始化：

可以在最前⾯加上⼀个「辅助结点」，帮助我们初始化。使⽤这种技巧要注意两个点：

辅助结点里面的值要「保证后续填表是正确的」。
「下标的映射关系」。

在本题中，需要「加上⼀行」，并且「加上两列」。所有的位置都初始化为无穷大，然后将第⼀行初始化为 0 即可。

#：填表顺序：

根据「状态表示」，填表的顺序是「从上往下」。

#：返回值：

注意：这里不是返回 dp[m][n] 的值！题目要求「只要到达最后一行」就行了，因此这里应该返回「 dp 表中最后一行的最小值」。

C++ 算法代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int row = matrix.size();
        int col = matrix[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(row + 1, vector<int>(col + 2, INT_MAX));

        // 2、初始化
        for(int i = 0; i < col + 2; i++)
            dp[0][i] = 0;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
        {
            for(int j = 1; j < col + 1; j++)
            {
                dp[i][j] = matrix[i - 1][j - 1] + min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i - 1][j + 1]));
            }
        }

        return *min_element(dp[row].begin(), dp[row].end());
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n*m)。

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int minFallingPathSum(vector<vector<int>>& matrix) {
        int row = matrix.size();
        int col = matrix[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(2, vector<int>(col + 2, INT_MAX));

        // 2、初始化
        for(int i = 1; i < col + 1; i++)
            dp[0][i] = 0;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
        {
            for(int j = 1; j < col + 1; j++)
            {
                int tmp_i = i % 2;
                int before_i = (i + 1) % 2;
                dp[tmp_i][j] = matrix[i - 1][j - 1] + min(dp[before_i][j - 1], min(dp[before_i][j], dp[before_i][j + 1]));
            }
        }

        // 4、返回值
        return *min_element(dp[row % 2].begin(), dp[row % 2].end());
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n)。

最小路径和⭐⭐

64. 最小路径和 - 力扣（LeetCode）

【算法原理】

#：状态表示：

对于这种「路径类」的问题，我们的状态表示⼀般有两种形式：

从 [i, j] 位置出发，……；
从起始位置出发，到达 [i, j] 位置，……。

这里选择第二种定义状态表示的方式： dp[ i ][ j ] 表示：走到 [ i, j ] 位置处，最小路径和是多少。

#：状态转移方程：

如果 dp[ i ][ j ] 表示到达 [ i, j ] 位置的方法数，那么到达 [ i, j ] 位置之前的⼀小步，有两种情况：

从 [i - 1, j] 向下走一步，转移到 [i, j] 位置
从 [i, j - 1] 向右走一步，转移到 [i, j] 位置

由于到 [ i, j ] 位置两种情况，并且我们要找的是最小路径，因此只需要这两种情况下的最小值，再加上 [ i, j ] 位置上本⾝的值即可。

也就是状态转移方程为：dp[ i ][ j ] = min(dp[ i - 1 ][ j ], dp[ i ][ j - 1 ]) + grid[ i ][ j ] 。

#：初始化：

对第一行，第一列继续初始化，由于 dp[ 0 ][ j ] 只能由前所来，dp[ i ][ 0 ] 只能由上所来。

#：填表顺序：

根据「状态转移方程」的推导来看，填表的顺序就是「从上往下」填每⼀行，在填写每⼀行的时候「从左往右」。

#：返回值：

根据「状态表示」，我们要返回 dp[m - 1][n - 1] 的值。

C++ 算法代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(row, vector<int>(col, 0));
        
        // 2、初始化
        dp[0][0] = grid[0][0];
        for(int i = 1; i<col; i++)
            dp[0][i] = dp[0][i - 1] + grid[0][i];
        
        for(int i = 1; i<row; i++)
            dp[i][0] = dp[i - 1][0] + grid[i][0];

        // 3、填表
        for(int i = 1; i<row; i++)
            for(int j = 1; j<col; j++)
                dp[i][j] = grid[i][j] + min(dp[i - 1][j], dp[i][j - 1]);

        // 4、返回值
        return dp[row - 1][col - 1];
    }
};

复杂度分析

时间复杂度：O(n*m)，两层for循环。
空间复杂度：O(n*m)。

【DP边界、初始化】

极度类似于上述题型，但是不同的是此处要的是最小，于是需要将一行，一列先初始化为最大值201（此处由于dp其余范围初始值不重要，直接全最大值即可）。

然后便是利用 dp[ 0 ][ 1 ] = 1 / dp[ 1 ][ 0 ] = 1，于是推出有效范围中的第一个元素 [ 1 ][ 1 ]。然后利用第一行与第一列的201，一定大于有效范围中的有效值，保证可以在填表环节中不越界的运算。

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<vector<int>> dp(row + 1, vector<int>(col + 1, 201));
        
        // 2、初始化
        dp[0][1] = 0;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
            for(int j = 1; j < col + 1; j++)
                dp[i][j] = grid[i - 1][j - 1] + min(dp[i - 1][j], dp[i][j - 1]);

        // 4、返回值
        return dp[row][col];
    }
};

【空间优化 - 滚动数组】

C++ 算法代码

class Solution {
public:
    int minPathSum(vector<vector<int>>& grid) {
        int row = grid.size();
        int col = grid[0].size();

        // 1、创建dp表
        vector<int> dp(col + 1, 201);
        
        // 2、初始化
        dp[1] = 0;

        // 3、填表
        for(int i = 1; i < row + 1; i++)
            for(int j = 1; j < col + 1; j++)
                dp[j] = grid[i - 1][j - 1] + min(dp[j], dp[j - 1]);

        // 4、返回值
        return dp[col];
    }
};