1 理论基础
粒子群算法(particle swarm optimization,PSO)是计算智能领域,除了蚁群算法、鱼群算法之外的一种群体智能的优化算法。该算法最早由Kennedy和Eberhart在1995年提出的。PSO算法源于对鸟类捕食行为的研究,鸟类捕食时,找到食物最简单有效的策略就是搜寻当前距离食物最近的鸟的周围区域。PSO算法是从这种生物种群行为特征中得到启发并用于求解优化问题的,算法中每个粒子都代表问题的一个潜在解,每个粒子对应一个由适应度函数决定的适应度值。粒子的速度决定了粒子移动的方向和距离,速度随自身及其他粒子的移动经验进行动态调整,从而实现个体在可解空间中的寻优。
PSO算法首先在可行解空间中初始化一群粒子,每个粒子都代表极值优化问题的一个潜在最优解,用位置、速度和适应度值三项指标表示该粒子特征,适应度值由适应度函数计算得到,其值的好坏表示粒子的优劣。粒子在解空间中运动,通过跟踪个体极值Pbest和群体极值Gbest更新个体位置。个体极值Pbest是指个体所经历位置中计算得到的适应度值最优位置,群体极值Gbest是指种群中的所有粒子搜索到的适应度最优位置。粒子每更新一次位置,就计算一次适应度值,并且通过比较新粒子的适应度值和个体极值、群体极值的适应度值更新个体极值Pbest和群体极值Gbest位置。

2 案例背景
2.1 问题描述
本案例寻优的非线性函数为
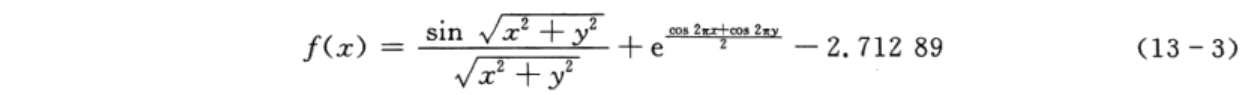
matlab绘图代码和图像如下:
[x,y]=meshgrid(-1.2:0.01:1.2);
z=sin( sqrt(x.^2+y.^2) )./sqrt(x.^2+y.^2)+exp((cos(2*pi*x)+cos(2*pi*y))/2)-2.71289;
mesh(x,y,z)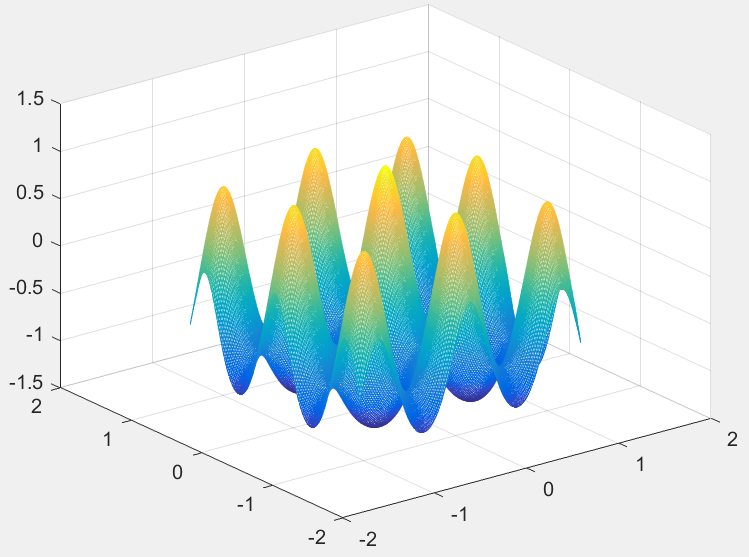
从函数图形可以看出,该函数有很多局部极大值点,而极限位置为(0,0),在(0,0)附近取得极大值。
2.2 解题思路及步骤
基于PSO算法的函数极值寻优算法流程图如图2所示。

其中,粒子和速度初始化随机初始化粒子速度和粒子位置;根据式(13-3)计算粒子适应度值;根据初始粒子适应度值确定个体极值和群体极值;根据式(13-1)与式(13-2)更新粒子速度和位置;根据新种群中粒子适应度值更新个体极值和群体极值。
本案例中,适应度函数为函数表达式,适应度值为函数值。种群粒子数为20,每个粒子的维数为2,算法迭代进化次数为300。
3 MATLAB程序实现
根据PSO算法原理,在MATLAB中编程实现基于PSO算法的函数极值寻优算法。
%% 清空环境
clc
clear
%% 参数初始化
%粒子群算法中的两个参数
c1 = 1.49445;
c2 = 1.49445;
maxgen=300; % 进化次数
sizepop=20; %种群规模
Vmax=0.5;
Vmin=-0.5;
popmax=2;
popmin=-2;
%% 产生初始粒子和速度
for i=1:sizepop
%随机产生一个种群
pop(i,:)=2*rands(1,2); %初始种群
V(i,:)=0.5*rands(1,2); %初始化速度
%计算适应度
fitness(i)=fun(pop(i,:)); %染色体的适应度
end
%% 个体极值和群体极值
[bestfitness bestindex]=max(fitness);
zbest=pop(bestindex,:); %全局最佳
gbest=pop; %个体最佳
fitnessgbest=fitness; %个体最佳适应度值
fitnesszbest=bestfitness; %全局最佳适应度值
%% 迭代寻优
for i=1:maxgen
for j=1:sizepop
%速度更新
V(j,:) = V(j,:) + c1*rand*(gbest(j,:) - pop(j,:)) + c2*rand*(zbest - pop(j,:));
V(j,find(V(j,:)>Vmax))=Vmax;
V(j,find(V(j,:)<Vmin))=Vmin;
%种群更新
pop(j,:)=pop(j,:)+V(j,:);
pop(j,find(pop(j,:)>popmax))=popmax;
pop(j,find(pop(j,:)<popmin))=popmin;
%适应度值
fitness(j)=fun(pop(j,:));
end
for j=1:sizepop
%个体最优更新
if fitness(j) > fitnessgbest(j)
gbest(j,:) = pop(j,:);
fitnessgbest(j) = fitness(j);
end
%群体最优更新
if fitness(j) > fitnesszbest
zbest = pop(j,:);
fitnesszbest = fitness(j);
end
end
yy(i)=fitnesszbest;
end
%% 结果分析
plot(yy)
title('最优个体适应度','fontsize',12);
xlabel('进化代数','fontsize',12);ylabel('适应度','fontsize',12);
最优个体适应度值变化如图3所示。

最终得到的最优个体适应度值为1.0053,对应的粒子位置为(0.0015,-0.0008),PSO 算法寻优得到最优值接近函数实际最优值,说明PSO算法具有较强的函数极值寻优能力。
4 延伸阅读
4.1 惯性权重的选择
惯性权重w体现的是粒子继承先前的速度的能力,Shi.Y最先将惯性权重引入PSO算法中,并分析指出一个较大的惯性权值有利于全局搜索,而一个较小的惯性权值则更利于局部搜索。为了更好地平衡算法的全局搜索与局部搜索能力,Shi.Y提出了线性递减惯性权重(linear decreasing inertia weight,LDIW),即

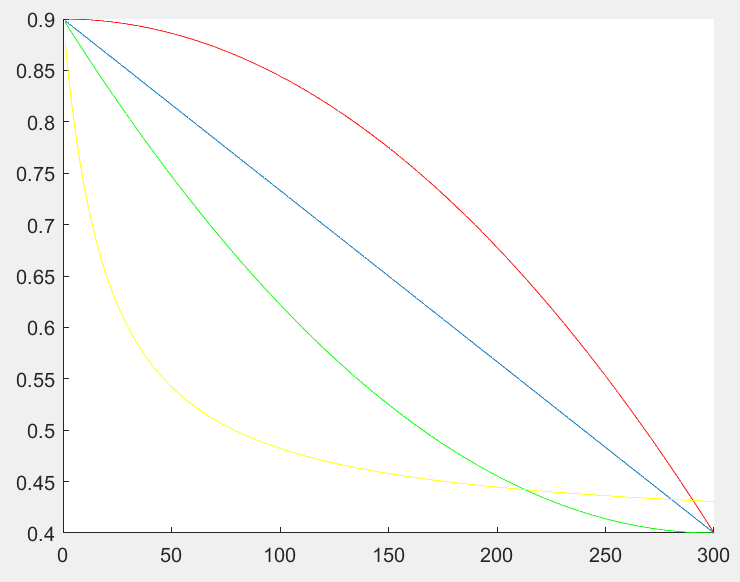
4.2 w变化的算法性能分析
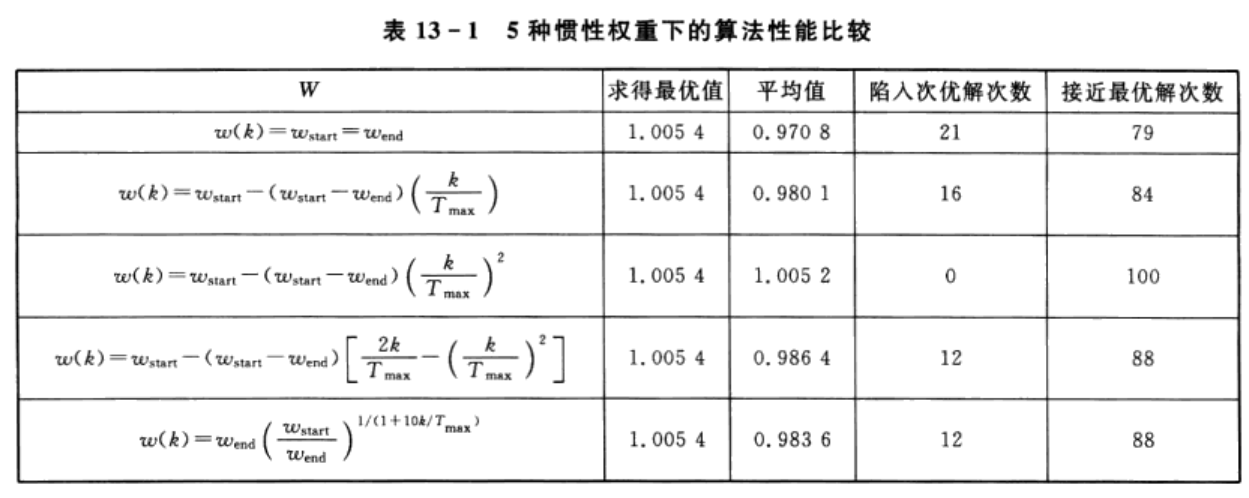
算法参数设置:种群规模20,进化300代。每个实验设置运行100次,将100次的平均值作为最终结果。在上述的参数设置下,运用5种w取值方法对函数进行求解,并比较所得解的平均值、失
效次数和接近最优值的次数,来分析其收敛精度、收敛速度等性能。每种w的算法进化曲线如图13-5所示。
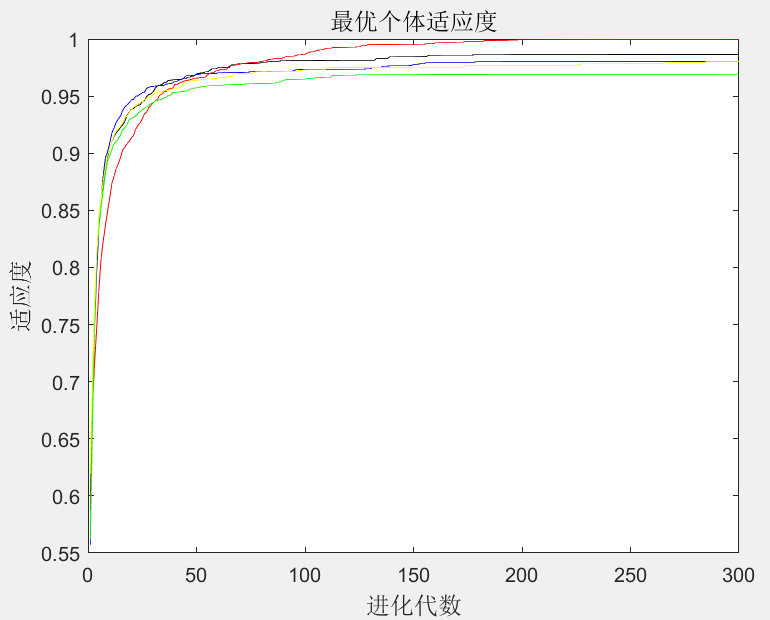
本案例中,将距离最优解1.0054误差为0.01的解视为接近最优解,将0.8477及更小的解视为陷入局部最优的解。
由图13-5和表13-1可以看出,惯性权重w不变的粒子群优化算法虽然具有较快的收敛速度,但其后期容易陷入局部最优,求解精度低;而几种w动态变化的算法虽然在算法初期收敛稍慢,但在后期局部搜索能力强,利于算法跳出局部最优而求得最优解,提高了算法的求解精度。
式(13-5)中w动态变化方法,前期w变化较慢,取值较大,维持了算法的全局搜索能力;后期w变化较快,极大地提高了算法的局部寻优能力,从而取得了很好的求解效果。