菜鸟的刷题之路之二叉树

news2024/11/27 4:31:04

💕“成功不是终点，失败不是终结，勇气才是启程的第一步。”💕
🐼作者：不能再留遗憾了🐼
🎆专栏：菜鸟的刷题之路🎆
🚗本文章主要内容：将有序数组转换为二叉搜索树、二叉搜索树中第K小的元素和叶子相似的树的详细题解🚗

文章目录

将有序数组转换为二叉搜索树
- 题目要求
- 做题思路
- 代码实现
二叉搜索树中第K小的元素
- 题目要求
- 做题思路
- 代码实现
叶子相似的树
- 题目要求
- 做题思路
- 代码实现

将有序数组转换为二叉搜索树

将有序数组转换为二叉搜索树（难度：简单）

题目要求

给你一个整数数组 nums ，其中元素已经按升序排列，请你将其转换为一棵高度平衡二叉搜索树。

高度平衡二叉树是一棵满足「每个节点的左右两个子树的高度差的绝对值不超过 1 」的二叉树。

示例：
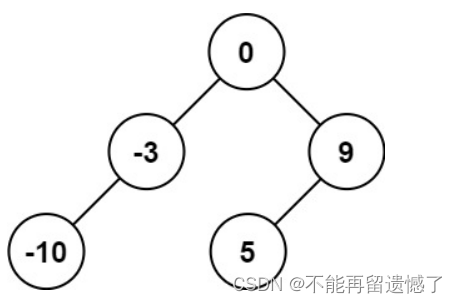
在这里插入图片描述

输入：nums = [-10,-3,0,5,9]
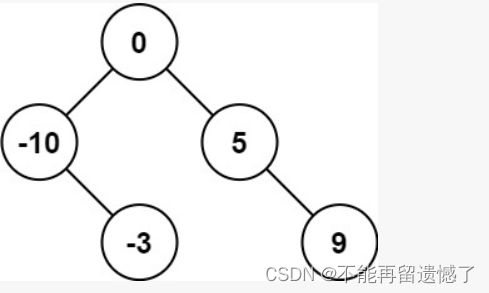
输出：[0,-3,9,-10,null,5]
解释：[0,-10,5,null,-3,null,9] 也将被视为正确答案：
在这里插入图片描述

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {

    }
}

做题思路

这个题目用到了二叉搜索树相关的知识，如果大家不了解或者忘记了，可以去看看这篇文章二叉搜索树。

二叉树是一种具有特殊性质的二叉树，它的根节点关键字总是大于左孩子的关键字，小于右孩子的关键字。并且这个题目是要求你将有序数组转换成一个高度平衡的二叉搜索树，所以我们就需要保证根节点的左右子树的高度差不超过一，那就是说我们可以每次取有序数组的最中间的值作为根节点，该中间值的左半部分作为左子树，右半部分作为右子树，然后重复进行该操作。

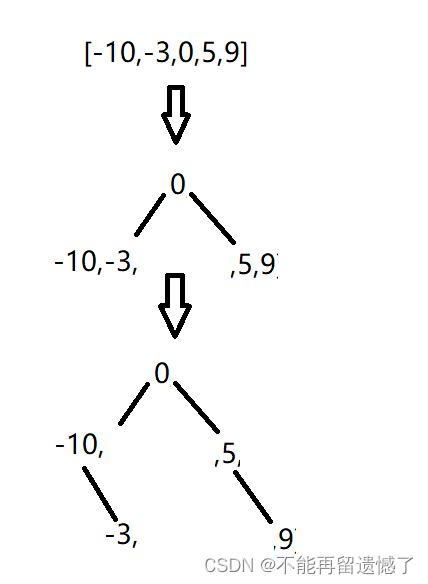
在这里插入图片描述

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public TreeNode sortedArrayToBST(int[] nums) {
        return sortedArrayToBSTChild(nums,0,nums.length-1);
    }

    public TreeNode sortedArrayToBSTChild(int[] nums,int left,int right) {
        if(left > right) return null;
        int mid = left + (right-left) / 2;
        TreeNode root = new TreeNode(nums[mid]);
        root.left = sortedArrayToBSTChild(nums,left,mid - 1);
        root.right = sortedArrayToBSTChild(nums,mid + 1,right);

        return root;
    }
}

在这里插入图片描述

二叉搜索树中第K小的元素

二叉搜索树中第K小的元素（难度：中等）

题目要求

给定一个二叉搜索树的根节点 root ，和一个整数 k ，请你设计一个算法查找其中第 k 个最小元素（从 1 开始计数）。

示例：
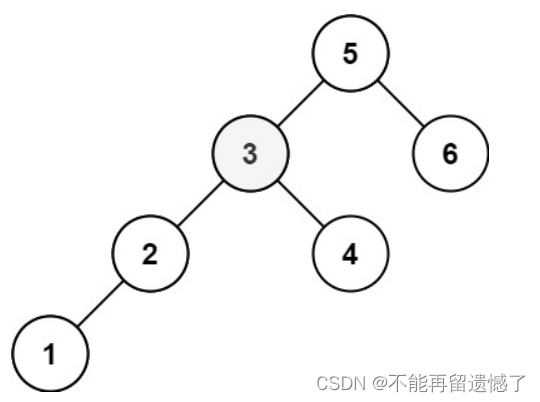
在这里插入图片描述

输入：root = [5,3,6,2,4,null,null,1], k = 3
输出：31

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {

    }
}

做题思路

因为二叉搜索数的根节点的关键字总是大于左孩子的关键字，小于右孩子的关键字，所以我们可以先在根节点的左树中查找是否存在第 k个最小元素，如果不存在就看根节点是否是最小的第 k 个最小元素，最后在右子树中查找。在查找子树的过程中同样是左孩子 - 根节点 -右孩子的顺序查找。要想实现这种功能，我们需要借助栈这种数据结构，将从根节点到最左边的左孩子节点路径上的节点放入栈中，那么栈顶的元素总是栈中最小的数据，当左孩子不是我们要找的节点时，就看根节点，最后是右孩子。

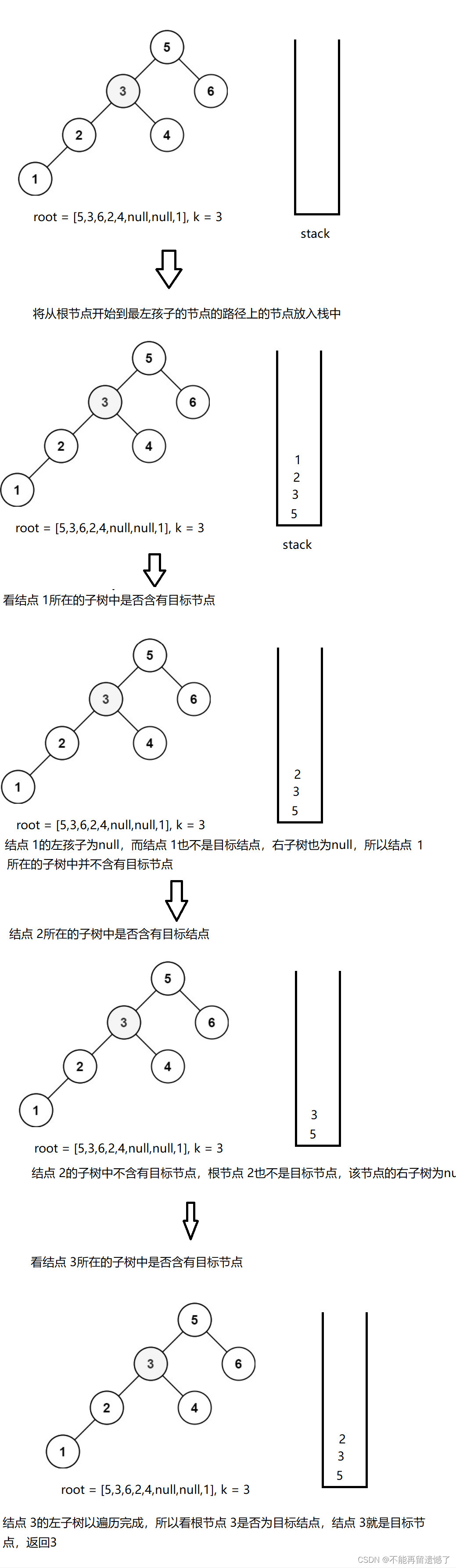
在这里插入图片描述

以上思路就是递归的大概思路

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public int kthSmallest(TreeNode root, int k) {
        Stack<TreeNode> stack = new Stack<>();
        while(root != null || !stack.empty()) {
            while(root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if(--k == 0) break;
            root = root.right;
        }

        return root.val;
    }
}

在这里插入图片描述

叶子相似的树

叶子相似的树（难度：简单）

题目要求

请考虑一棵二叉树上所有的叶子，这些叶子的值按从左到右的顺序排列形成一个叶值序列。
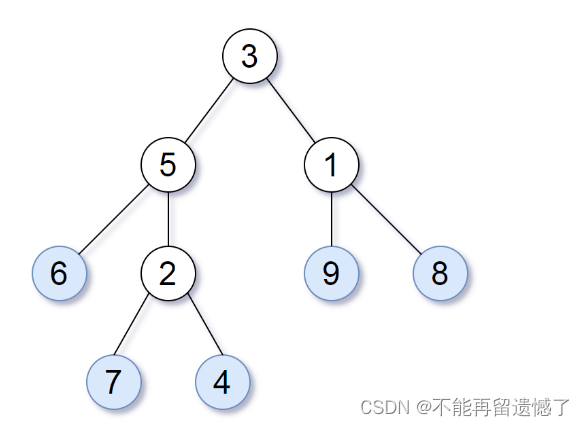
在这里插入图片描述

举个例子，如上图所示，给定一棵叶值序列为 (6, 7, 4, 9, 8) 的树。

如果有两棵二叉树的叶值序列是相同，那么我们就认为它们是叶相似的。

如果给定的两个根结点分别为 root1 和 root2 的树是叶相似的，则返回 true；否则返回 false 。

示例：
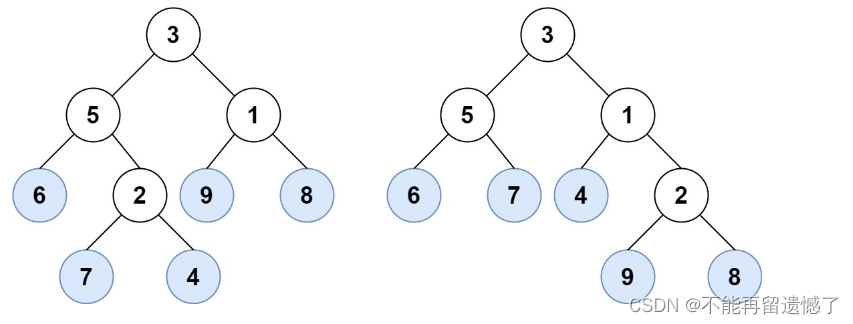
在这里插入图片描述

输入：root1 = [3,5,1,6,2,9,8,null,null,7,4], root2 = [3,5,1,6,7,4,2,null,null,null,null,null,null,9,8]
输出：true

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean leafSimilar(TreeNode root1, TreeNode root2) {

    }
}

做题思路

这个题目我们可以参考上面的一个题目，采用中序遍历的方法，判断该节点是否为叶子节点，如果是，就把它放入链表中。分别遍历这两个树，将叶子节点放入链表中，然后看这两个链表是否相同。

代码实现

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public boolean leafSimilar(TreeNode root1, TreeNode root2) {
        if(root1 == null || root2 == null) return false;
        List<TreeNode> list1 = new ArrayList<>();
        List<TreeNode> list2 = new ArrayList<>();
        leafSimilarChild(root1,list1);
        leafSimilarChild(root2,list2);
        if(list1.size() != list2.size()) return false;
        for(int i = 0; i < list1.size(); ++i) {
            if(list1.get(i).val != list2.get(i).val) return false;
        }

        return true;
    }

    private void leafSimilarChild(TreeNode root,List<TreeNode> list) {
        if(root == null) return;
        leafSimilarChild(root.left,list);
        if(root.left == null && root.right == null) list.add(root);
        leafSimilarChild(root.right,list);
    }
}