2. IMU原理及姿态融合算法详解

一、组合

IMU全称是惯性导航系统，主要元件有陀螺仪、加速度计和磁力计。其中，陀螺仪可以得到各个轴的加速度，而加速度计能够得到$x$、$y$、$z$方向的加速度，而磁力计能获得周围磁场的信息。

主要的工作便是将三个传感器的数据融合得到较为准确的姿态信息。

二、 原理

a) 陀螺仪

陀螺仪是通过测量科氏力来检测角速度的，科氏力在大学物理中提到过，如下图：

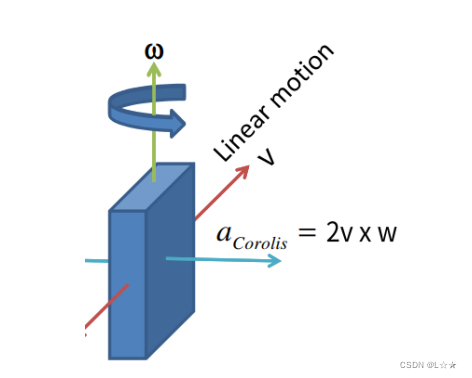
一个物体以固定的线速度$v$ 运动，同时受到一个角速度的影响，这时候在叉乘方向上会有一个科氏力的作用，测量这个力便能直到角速度 $w$ 的大小。

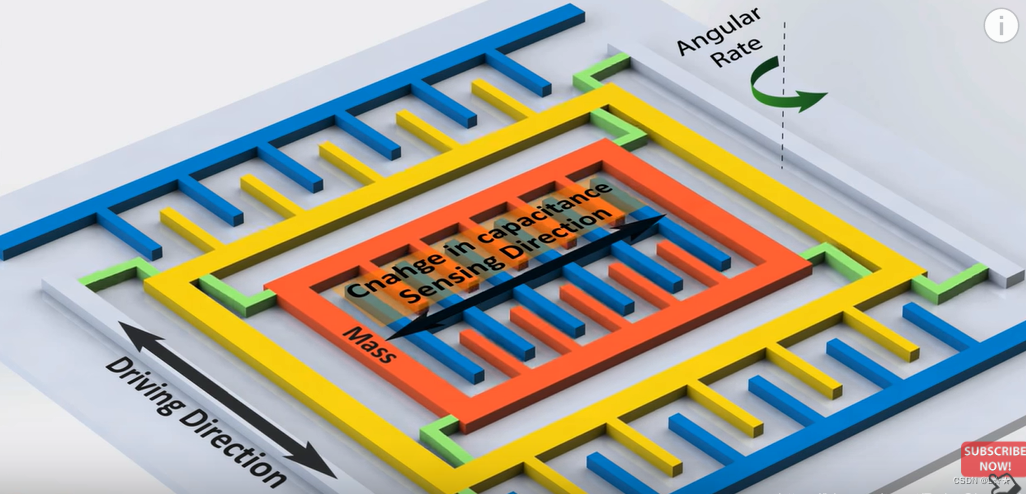
在实际的MEME传感器中，大致结构如图，在一个方向保持左右运动。若有旋转的角速度则会在垂直的方向产生科氏力，通过电容的变化来反应这个力的大小便能得到旋转速度的大小。

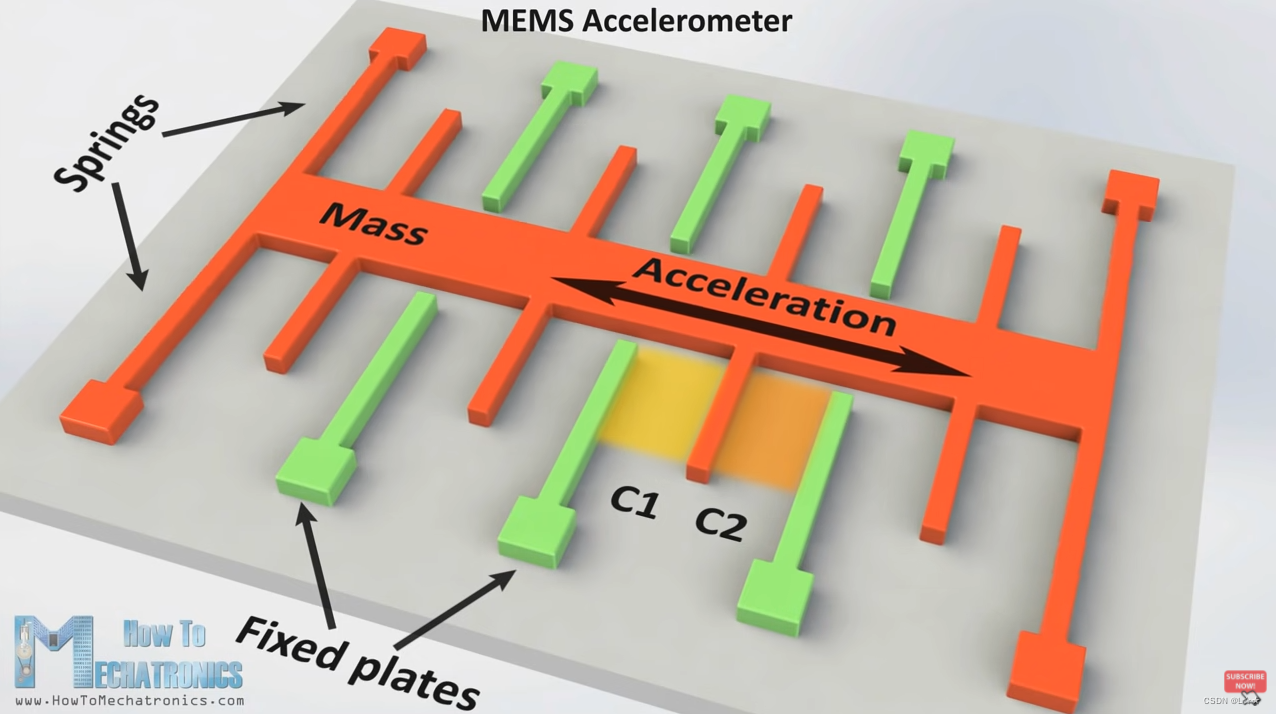
b) 加速度计

加速度计的原理较为简单，就是通过牛顿第二定律来测量三轴的加速度。图中的质量块受到加速度的作用会左右运动，而两侧的电容能测量质量块的位置，从而计算出加速度的大小。

c) 磁力计

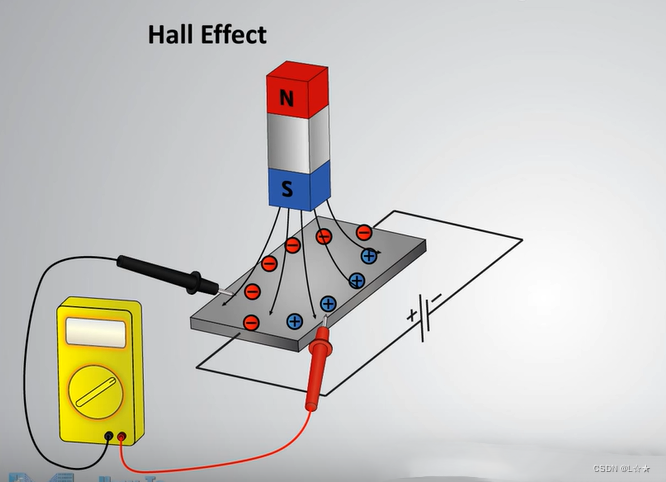
磁力计则是通过霍尔效应来测量磁场的强度，高中物理中学过霍尔效应也很简单，如图。一端通电，在磁场的作用下电子会往垂直的方向上跑，从而在侧面产生电场，通过测量这个电场的强度及正负则能间接测量出厂强的大小。

视频介绍如下： https://www.youtube.com/watch?v=eqZgxR6eRjo&feature=youtu.be

三、 旋转的表达

a) 欧拉角

对姿态的描述，最直观的便是欧拉角。可以用维基百科上的一张动图直观的表示：

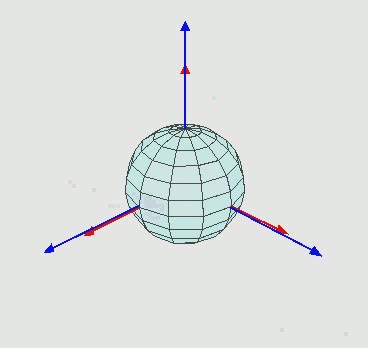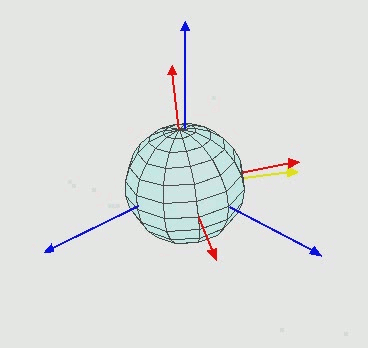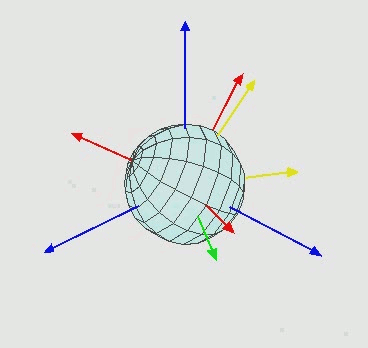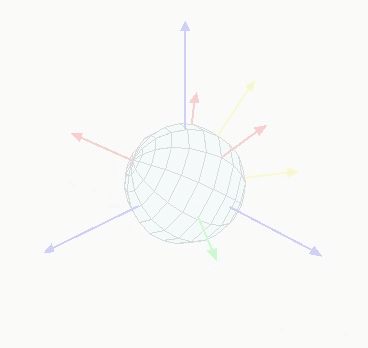
b) 旋转矩阵

线性代数中，有讲解过，使用 $3\times 3$ 的矩阵可以表达物体的旋转，如绕 $Z$ 轴的旋转可以表示为：
$$\left[\begin{array}{c}{x}^{{}^{\prime }}\\ y^{{}^{\prime }}\\ z^{{}^{\prime }}\\ 1\end{array}\right]=\left[\begin{array}{cccc}\cos \theta & -\sin \theta & 0& 0\\ \sin theta& \cos \theta & 0& 0\\ 0& 0& 1& 0\\ 0& 0& 0& 1\end{array}\right]\cdot \left[\begin{array}{c}x\\ y\\ z\\ 1\end{array}\right]\text{\hspace{1em}(1)}$$
其他轴旋转可以自行百度。

c) 四元数

四元数的运算表达比较难理解，但是在数学上却可以优雅而完美的表达三维空间中的旋转。它可以很好的避免欧拉角存在的万向锁问题，和轴角存在的不适合插值的缺点，同时它所需的参数量较少，因此现有的大部分效果较好的解法都是采用四元数解算的。

这里主要介绍如何通过四元数来更新姿态：

已知当前姿态为四元数$q_1$ ，在$\Delta t$ 时间内的角速度为 $\omega$， 求下一刻的四元数。

一般来说，采用一阶龙格库塔法来更新四元数，主要的思路便是 泰勒展开式，然后一阶近似。

具体计算流程如下：
$${\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]}_{t+\Delta t}={\left[\begin{array}{c}{q}_0\\ q_1\\ q_2\\ q_3\end{array}\right]}_t+\frac{\Delta t}{2}\left[\begin{array}{c}-{\omega }_x{q}_1-{\omega }_y{q}_2-{\omega }_z{q}_3\\ {\omega }_x{q}_0+{\omega }_z{q}_2-{\omega }_y{q}_3\\ {\omega }_y{q}_0-{\omega }_z{q}_1+{\omega }_x{q}_3\\ {\omega }_z{q}_0+{\omega }_y{q}_1-{\omega }_x{q}_2\end{array}\right]\text{\hspace{1em}(2)}$$

d) 李群 $\text{SO}(3)$ 及 李代数 $\text{so}(3)$

对于这两种表达方法在主流陀螺仪的姿态解算中并不常见，但是在某些算法中需要对姿态进行求导时，便需要采用李群的方法去表达姿态。

比如对旋转的求导如下：
$$\begin{array}{rl}\frac{\partial \text{Rp}}{\partial \phi }& =\underset{\phi \to 0}{\lim }\frac{\exp ({\phi }^{\wedge })\exp ({\varphi }^{\wedge })\text{p}-\exp ({\varphi }^{\wedge })\text{p}}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{\text{I}+{\phi }^{\wedge }\exp ({\phi }^{\wedge })\text{p}-\exp ({\phi }^{\wedge })\text{p}}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{{\phi }^{\wedge }\text{Rp}}{\phi }\\ & =\underset{\phi \to 0}{\lim }\frac{-(\text{Rp}{)}^{\wedge }\phi }{\phi }\\ & =-(\text{Rp}{)}^{\wedge }\end{array}\text{\hspace{1em}(3)}$$

具体可参考高翔博士的《视觉SLAM 14讲》

博客：https://www.cnblogs.com/gaoxiang12/p/5137454.html

视频：https://www.bilibili.com/video/BV16t411g7FR?p=3&vd_source=484659340e491a658a0140936c410c09

个人笔记：https://blog.csdn.net/weixin_43662553/article/details/128161000?spm=1001.2014.3001.5502

四、 传感器的噪声及去除

传感器噪声，一般分为两种：

• 随机噪声：一般认为随机噪声是符合高斯分布的
• 固定误差：固定误差是由于传感器的测量原理导致的，这部分通常是去噪的重点。实际上，由于制造和安装误差，会有许许多多的固定误差。但是由于使用要求不高，且大部分校准需要高精度转台，只能做较为简单的校准工作。

a) 陀螺仪

陀螺仪直接测量的是角速度而非角度，所以需要通过一次积分才能得到角度值。

在积分过程中，若有固定的、某一个方向的数据，则会在积分的过程中，不断加大影响导致角度偏差。

通常来说，陀螺仪的温漂是比较严重的，基本上温漂正比于芯片的价格，越贵的芯片漂的越少。温漂的数据既与温度相关，又与时间相关。也就是说，不同温度下不一样，不同上电时间下也不一样。

通常简单的做法是：在上电的时候静止一段时间计算出此时的零偏，然后每次减去零偏。

更高级的方法需要标定温度与零偏的关系，然后线性插补；另一方面使用艾伦方差分析法得到零偏和时间的关系（艾伦方差法见博客https://blog.csdn.net/yandld/article/details/81101984）。

对于其他的误差，比如三轴不相互垂直，以及尺度因子不一致等误差，都可以忽略。

当然，更好的情况是在电路上做一个温度控制，维持在温度$50°$ 左右（必须要在常温以上）。

b) 加速度计

对于加速度计，同样会有零漂和尺度因子的误差，但是加速度计在静止时可直接得到角度而不需要积分，所以零漂的影响很小，但是尺度因子的影响较大。

同样是重力加速度，各个面朝下时检测到的数值是不一样的。一般来说，校准的方法有六面校准。 就是各个面朝下，然后记录重力的数值，计算得到尺度因子。目前MEMS传感器的精度已经很高了，很多情况下只用正面朝上校准一次即可（仅适用于无人机）。

若要求不高，可以不去校准加速度计，而对于云台有其他的校准思路。

c) 磁力计

磁力计的数据误差较大，校准便显得很重要。

一般可以导出数据到MATLAB中，然后采用 椭球校准的方法 。但是这样比较麻烦，主要用于写论文…

而大多数飞控的做法，都是直接在单片机上处理的，步骤如下：

• 先头朝上，水平旋转一周
• 然后头朝下，再水平旋转一周。
• 若计算能力有限，可直接求最大最小数据的中值，得到偏差，然后计算幅值，

save.mag_offset[i] = 0.5f *(max_t[i] + min_t[i]);//中值校准
save.mag_gain[i] = safe_div(200.0f ,(0.5f *(max_t[i] - min_t[i])),0);//幅值校准

• 若计算能力较充裕，采用LM算法可计算出三维的偏差和三维的尺度因子，具体参考天穹飞控代码。

五、姿态解算原理

IMU的算法紧紧地围绕着如何利用这三个元器件，获得准确的姿态，基本要求有几点：

• 滞后效应不明显
• 角度准确
• 静止时角度不漂

但很多时候，都无法满足所有的要求，需要根据实际情况的需求来有所取舍。

a) 陀螺仪

陀螺仪获得角度的方法很简单，直接积分就好了。但是直接积分会带来巨大的误差！！

第一个原因如图所示：

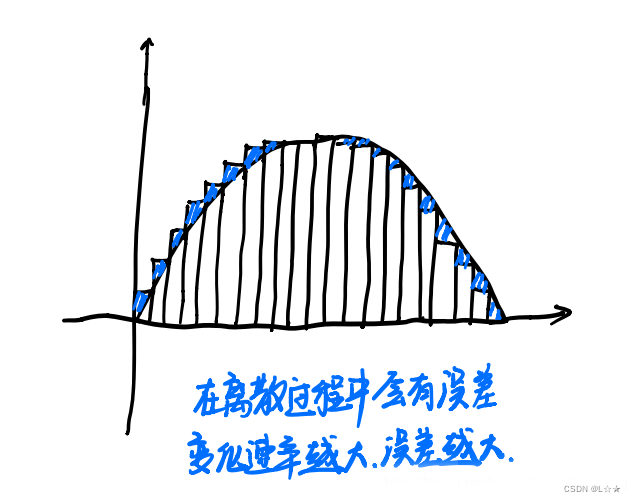
解决方法如下，采用中值积分：

另一个方面，陀螺仪得到的旋转数据是基于机体坐标系的，而我们要求的是世界坐标系下的姿态，这中间必然有一个坐标变换的关系：
$$\left[\begin{array}{c}{\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right]=\left[\begin{array}{ccc}\cos \gamma & 0& -\cos \theta \sin \gamma \\ 0& 1& \sin \theta \\ \sin \gamma & 0& \cos \cos \gamma \end{array}\right]\left[\begin{array}{c}\dot{\theta }\\ \dot{\gamma }\\ \dot{\psi }\end{array}\right]\stackrel{\theta ,\gamma \text{较小}}{⟶}\left[\begin{array}{c}\dot{\theta }\\ \dot{\gamma }\\ \dot{\psi }\end{array}\right]=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]\cdot \left[\begin{array}{c}\theta \\ \gamma \\ \psi \end{array}\right]+\left[\begin{array}{c}{\omega }_x\\ {\omega }_y\\ {\omega }_z\end{array}\right]$$
对于无人机来说，pitch和roll都比较小，可以认为是$0$，则旋转矩阵变为了单位矩阵。

但是对于云台和其他应用场景下，都很难做这个近似，写代码的时候切勿直接积分。

b) 加速度计

加速度计的作用便是直接测量出pitch和roll的角度，对积分得到的角度进行一个矫正。

基本原理见博客：http://www.starlino.com/imu_guide.html

一般情况下，网上都是采用互补滤波来综合加速度计角度不会漂，但噪声大；而陀螺仪角度精度却会漂的特点。

但加速度计计算角度的公式是有前提的：便是物体静止。而对于剧烈运动的物体则会引起巨大的误差，

这个时候有一个很重要的工作，就是做好加速度补偿，一般分为线加速度的补偿和角加速度的校准。

对于线加速度，很难得到有飞控源码中采用辅助姿态解算算法来做补偿（见天穹飞控源码），一般的处理方法可以计算角加速度计的模长，若越大，则加速度的置信度越小。

对于角加速度，可以通过陀螺仪来计算得到。

得到角加速度后，可以计算出切向加速度和法向加速度分别补偿。

c) 磁力计

磁力计可以看成一个指南针，可以对yaw轴 角度进行一个矫正。具体计算公式较为简单，但注意在套用公式前，需要对数据进行倾斜补偿。

具体见博客：https://blog.csdn.net/w8253497062015/article/details/79833321

还有一点需要注意的是：

在实际的工程源码中，通常都对公式进行了简化，这一点需要注意。

六、姿态解算算法

姿态解算算法五花八门，各种各样的都有，同一种算法还可以根据不同的旋转表达方法有不同的表达方式。

所以要用好一个算法需要对原理进行深入的了解，看到算法的最根本的东西，虽然很难，但必须要做。

a) 互补滤波

主要思想在于：把陀螺仪的高频部分和磁力计或加速度计的低频部分叠加在一起，得到更准确、更稳定的姿态。

b) AHRS

AHRS 一般有两种思路——Madgwick 和Mahony，具体的各种Google都可以得到。这里主要介绍各种思想：

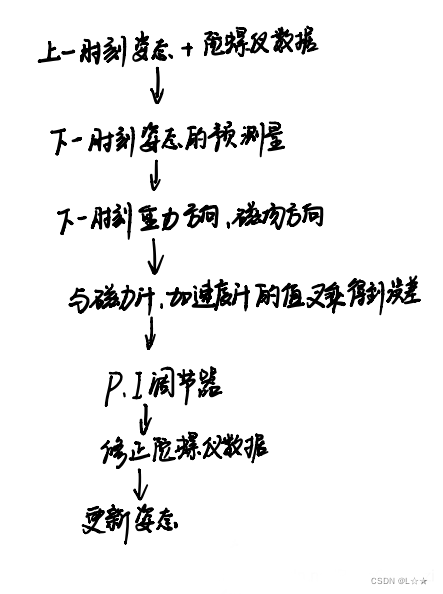
• 首先是飞机较常用的Mahony算法，算法应用在pix上较为成熟和经典

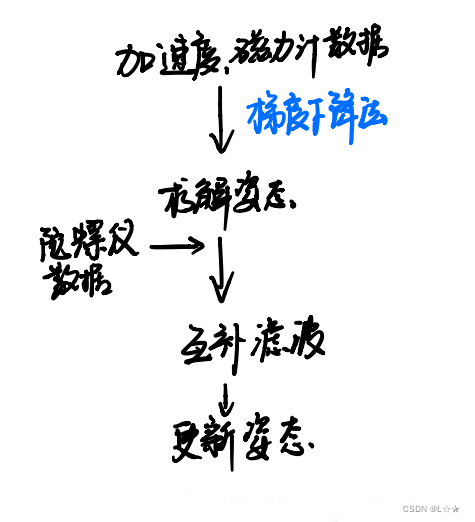
• 其次是，2012年开源出来的madgwick算法，效果更好计算量也更大

c) 卡尔曼

卡尔曼不仅仅用在陀螺仪的姿态解算上，所以对卡尔曼滤波本身的理解也十分重要。

推荐的网站有：https://nbviewer.org/github/rlabbe/Kalman-and-Bayesian-Filters-in-Python/blob/master/table_of_contents.ipynb

对于卡尔曼算法可以建立不同的模型，来估计当前姿态，其中一种较为直观的是互补滤波的推广。

• 预测量：陀螺仪的积分角度
• 观测量：加速度计和磁力计分别计算出的roll、pitch和yaw

七、 云台的特性及要求

1. roll轴角度几乎为零，而pitch轴角度较大
2. 安装位置不在中心，角加速度对加速度计的影响大
3. 机器人起停时，会有较大的线加速度，对加速度计影响大
4. yaw轴零点位置要求不严格，而pitch轴要求零点必须水平

对于云台的yaw轴，通常采用AHRS_Madgwick的思路，需要注意的是：

• 在动态情况下，原论文的互补滤波效果更好
• 在静态情况下，将互补滤波换为卡尔曼滤波更好

陀螺仪的算法基本可以参考Madgwick的算法思路，对陀螺仪算法最最重要的点在于：

• 利用现有的参数对算法进行较好的初始化
• 尽量根据使用场景情况，在算法推导过程中做简化，再根据自己的推导写代码
• 误差的校准，加速度的补偿