区分序列/UIO/特征集示例

从确定性有限状态机进行测试：检查状态

概述
让我们假设我们有一个状态集 S 的 FSM M。还假设我们知道通过转换 t 达到的当前状态是 s 或 s0。
我们如何确定 t 到达了哪个状态？

分离状态
输入序列 w 将两个状态 s 和 s0 分开，如果： 对 w 的响应在 s 和 s0 中不同。
更正式地说，我们要求：

方法
我们想要区分模拟被测系统的未知 FSM MI 的状态。
相反，我们设计了区分 M 状态的序列。
我们可以在检查 MI 的状态时使用这些。我们可能会使用以下之一：
一个区别序列A distinguishing sequence。
独特的输入/输出序列Unique input/output sequences。
一个特征集A characterising se。
理想情况下，测试检查序列（验证它们区分 MI 的状态）

区分序列
输入序列 D 是一个可区分序列，如果：
对于每对状态 s,s0 of M 使得 s /= s0，我们有 λ∗(s, D) /= λ∗(s0, D)。
这意味着：响应 D 产生的输出标识了 M 的状态。要检查转换 t 的最终状态，在 t 之后跟随 D 就足够了。

使用区分序列

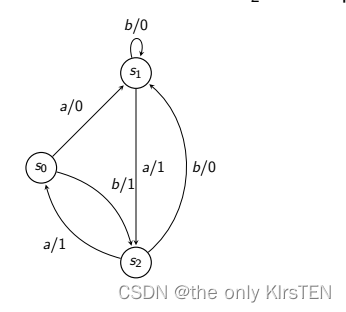
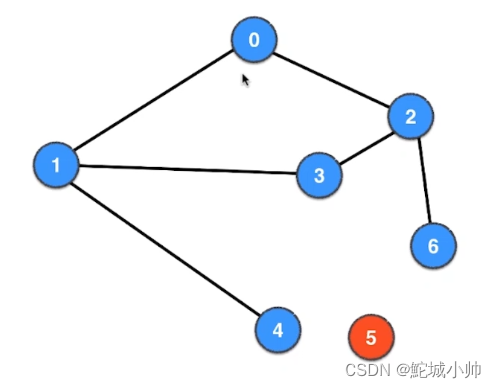
在该示例中，aa 形成一个可区分序列，因为：
从状态 s0 输出序列是 01
从状态 s1 输出序列为 11
从状态 s2 输出序列为 10

如果我们想检查转换 t = (s2, s1, b/0) 我们产生一个测试序列：
以诸如 b/1 的前导码开始，它将 M 带到 t 的起始状态。 接下来是来自 t 的输入/输出对 b/0。然后从结尾应用区分序列aa，得到a/1 a/1
连接这些，我们得到测试序列：b/1 b/0 a/1 a/1。

寻找区别序列
一些 FSM 没有区分序列。
没有有效的算法来决定 FSM 是否具有可区分序列（或生成可区分序列序列，当它们存在时）。但是，我们可以使用简单的搜索技术（例如广度优先）

独特的输入输出序列Unique Input Output Sequences (UIO)
输入/输出序列 x/y 是状态 s 的 UIO，如果：
y = λ∗(s, x) 并且对于 M 的每个状态 s0 使得 s /= s0 我们
有 λ∗(s0, x) /= λ∗(s, x)
这意味着输入 x 标识状态 s，因为：如果 y 是响应 x 产生的，我们一定处于状态 s，否则我们一定处于不同的状态。
注意：可区分序列标识所有状态，但 UIO 可能仅标识一个状态。

UIO 示例

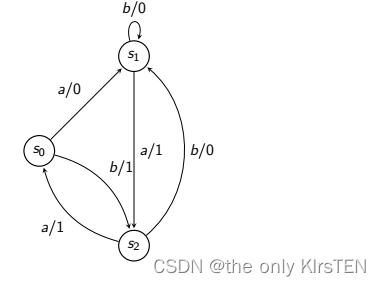
在示例中，a=0 为状态 s0 形成一个 UIO：
从状态 s0 输出序列为 0
从状态 s1 输出序列为 1
从状态 s2 输出序列为 1
请注意，a 不是可区分序列。

使用 UIO 测试转换transitions
为了测试转换 t = (s2, s0, a/1) 我们可以建立一个测试顺序如下：
到达初始状态 t 的前导码 b/1；
转换的输入/输出对 a/1。
最后，为转换的结束状态 (a/0) 选择的 UIO。
这给出了测试序列 b/1 a/1 a/0。

特征集Characterising Sets
一组 W 的输入序列是 M 的特征集，如果：
对于 M 的每对状态 s, s0 使得 s /= s0 我们有某些 w 属于 W，使得 λ∗(s, w) /= λ∗(s0, w)（即 w 区分这些状态）。
这意味着：对于每对状态，都有一些输入(W 区分它们的序列)。

使用特征集
如果我们知道来自 W 的每个输入序列触发的输出，我们就可以识别状态。
要检查转换 t = (si, sj, x/y) 我们可以分别在 t 后面跟上 W 的每个元素。因此，使用特征集会导致对转换进行多次测试。
注意：每个最小 FSM 都有一个特征集——而这些可以在多项式时间内找到。

特征集示例
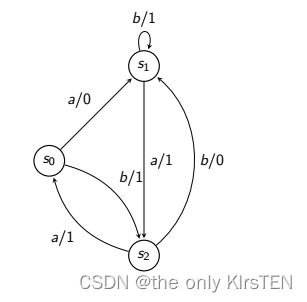
在这个 FSM 中，{a, b} 是一个特征集，因为：


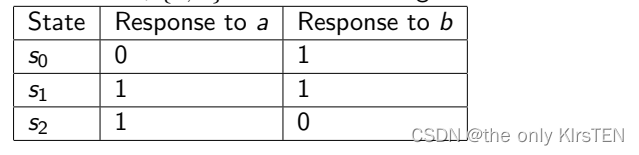
结果
对于这个例子，如果我们正在检查一个转换 t 的最终状态，我们分别在它后面跟上 a 和 b。
因此，我们使用两个测试进行转换。
如果在 t 之后对 a 的响应是 1，而在 t 之后对 b 的响应是 0，则转换必须将实现带到对应于 s2 的状态。

概括
如果我们只对资助输出故障感兴趣，那么简单地执行 M 的所有转换（transition tour）就足够了。
如果我们希望能够发现状态转移错误，那么我们需要使用区分状态的技术。
我们探索了三种备选方案：可区分序列、UIO 和特征集。
接下来我们会遇到一个同样寻找额外状态的方法