10.1 常用技巧

位运算 利用二进制位运算的特性进行优化和计算。

常用的位运算符号包括：^ 按位异或、& 按位与、| 按位或、~ 取反、<< 算术左移、>> 算术右移。

以下是一些常见的位运算特性，其中 0s 和 1s 分别代表只由 0 或 1 构成的二进制数字。

x ^ 0s = x 		x & 0s = 0		x | 0s = x

x ^ 1s = ~x 	x & 1s = x		x | 1s = 1s

x ^ x = 0 		x & x = x		x | x = x

除此之外， n & (n-1) 将 n 的二进制表示中的最低位为1的改为0，例如对于二进制表示 11110100，减一得到 11110011 ，这两个数按位与得到 11110000 。

n & (-n) 可以取得n 最右边的 1，例如对于二进制表示 11110100 ，取负得到 00001100 ， 按位与得到 00000100 。
注： 取负技巧是从左往右，直到遇到第一个 1 都保持不变，之后的数字都变成相反数。

10.2 位运算基础问题

461. 汉明距离（简单）

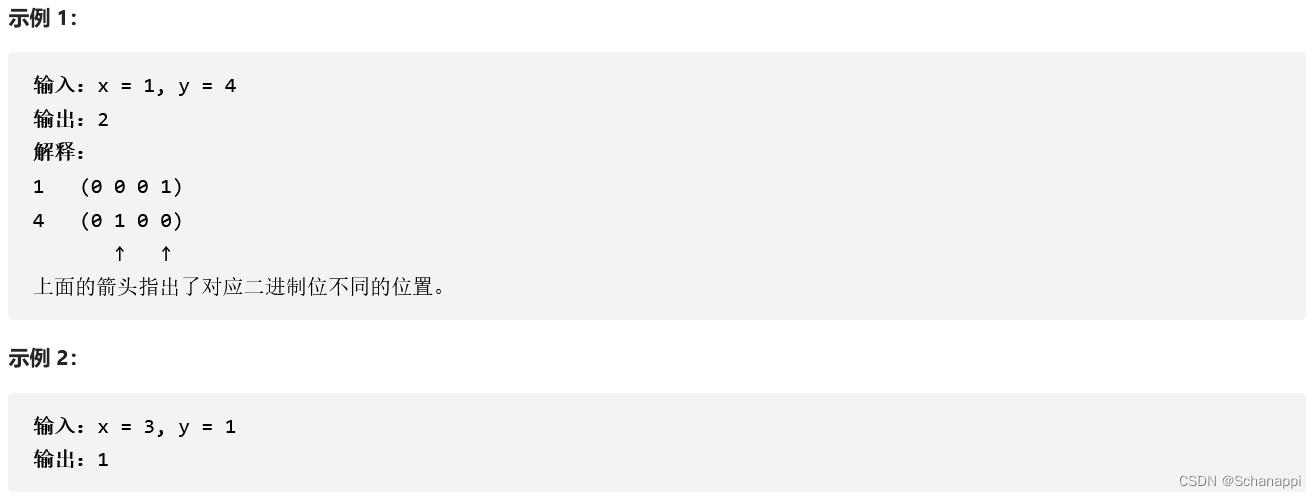
思路及代码： 461. 汉明距离

190. 颠倒二进制位（简单）

思路及代码： 190. 颠倒二进制位

136. 只出现一次的数字（简单）

思路及代码： 136. 只出现一次的数字

10.3 二进制特性

利用二进制的一些特性，我们可以把位运算使用到更多问题上。

例如，我们可以利用二进制和位运算输出一个数组的所有子集。假设我们有一个长度为 n 的数组，我们可以生成长度为 n 的所有二进制，1 表示选取该数字，0 表示不选取。这样我们就得到了 2ⁿ 个子集。

342. 4的幂（简单）

思路及代码： 342. 4的幂

318. 最大单词长度乘积（中等）

思路及代码： 318. 最大单词长度乘积

338. 比特位计数（简单）

思路及代码 ： 338. 比特位计数

10.4 练习

268. 丢失的数字（简单）

思路及代码： 268. 丢失的数字

693. 交替位二进制数（简单）

思路及代码： 693. 交替位二进制数

476. 数字的补数（简单）

思路及代码： 476. 数字的补数

260. 只出现一次的数字 III（中等）

思路及代码： 260. 只出现一次的数字 III