适用于所有 .NET 语言,包括 C#、Visual Basic 和 F#。
CenterSpace Software的NMath TM .NET 数学和统计库为.NET平台上的金融、工程和科学应用程序提供数值组件。

基础 .NET 数学和统计库NMath包括复数类、一般向量和矩阵类、结构化稀疏矩阵类和因式分解、一般稀疏矩阵类和因式分解、一般矩阵分解、最小二乘解、随机数生成器、快速傅里叶变换 (FFT)、数值积分和微分方法、函数最小化、曲线拟合、求根、线性和非线性规划。
此外,还支持数百个统计例程,包括数十个概率密度函数 (PDF)、描述性统计、线性回归、假设检验、方差分析 (ANOVA)、主成分分析、非负矩阵分解 (NMF)、偏最小二乘法(PLS)、数据过滤、Savizy-Golay 拟合和平滑以及许多其他例程。
方差分析
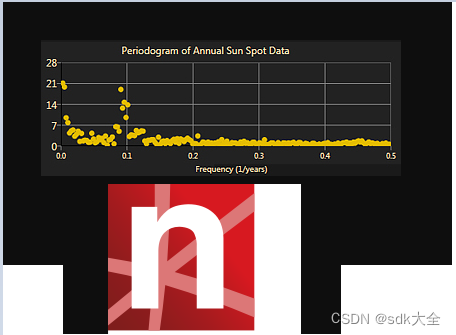
快速傅里叶变换
假设检验
线性规划
线性回归
主成分分析
概率分布
随机数发生器
矢量随机数
N数学
所有NMath例程都可以从任何 .NET 语言调用,包括 C#、Visual Basic.NET 和 F#。
对于许多计算, NMath 使用英特尔® 数学核心函数库 (MKL),它包含高度优化、广泛线程版本的 C 和 FORTRAN 公共领域计算包,称为 BLAS(基本线性代数子例程)和 LAPACK(线性代数包裹)。这为 NMath 例程提供了您可以信赖的准确性,以及 与 C 或 Fortran 相当的性能 水平。我们最先进的面向对象的界面易于使用,并充分利用了 .NET 平台的全部功能。
可以通过我们安全的在线商店下订单 。我们的 销售人员 可以帮助您解决有关我们产品的任何问题。另请参阅我们的常见问题列表。
NMath 特性总结
基础数学
单精度和双精度复数类。
用于各种概率分布的随机数生成器,使用 skip-ahead 和 leapfrog 方法的独立随机数流,以及使用 Niederreiter 和 Sobol 方法的拟随机序列。
快速傅里叶变换(FFT)、小波以及线性卷积和相关。
特殊函数,例如阶乘函数、二项式函数、伽马函数和相关函数、贝塞尔函数、椭圆积分等等。
线性代数
四种数据类型的全功能向量和矩阵类:单精度和双精度浮点数,以及单精度和双精度复数。
使用切片和范围的灵活索引。
对于支持它们的 .NET 语言,重载算术运算符具有它们的常规含义,对于不支持它们的那些具有等效命名方法(、等)。Add()Subtract()
全功能结构化稀疏矩阵类,包括三角形、对称、厄米特矩阵、带状矩阵、三对角矩阵、对称带状矩阵和厄米特带状矩阵。
用于在一般矩阵和结构化稀疏矩阵类型之间进行转换的函数。
用于转置结构化稀疏矩阵、计算内积和计算矩阵范数的函数。
分解结构化稀疏矩阵的类,包括带状和三对角矩阵的 LU 分解、对称和 Hermitian 矩阵的 Bunch-Kaufman 分解,以及对称和 Hermitian 正定矩阵的 Cholesky 分解。构造后,矩阵分解可用于求解线性系统并计算行列式、逆矩阵和条件数。
一般稀疏向量和矩阵类,以及矩阵分解。
一般矩阵的正交分解类,包括 QR 分解和奇异值分解 (SVD)。
一般矩阵的高级最小二乘分解类,包括 Cholesky、QR 和 SVD。
一般矩阵的 LU 因式分解,以及求解线性系统、计算行列式、逆矩阵和条件数的函数。
用于解决对称、厄米特和非对称特征值问题的类。
扩展标准数学函数,例如 Cos()、Sqrt() 和 Exp(),以处理向量、矩阵和复数类。
功能
用于封装一个变量的函数的类,支持数值积分(Romberg 和 Gauss-Kronrod 方法)、微分(Ridders 方法)和函数的代数操作。
多项式封装、插值和精确微分和积分。
使用黄金分割搜索和布伦特方法最小化单变量函数的类。
使用下坡单纯形法、鲍威尔方向集法、共轭梯度法和变量度量(或拟牛顿)法最小化多元函数的类。
模拟退火。
使用 Microsoft Solver Foundation 的线性规划(LP)、非线性规划 (NLP) 和二次规划 (QP)。
最小二乘多项式拟合。
非线性最小二乘最小化、曲线拟合和曲面拟合。
使用正割法、Ridders 法和 Newton-Raphson 法求单变量函数根的类。
双变量函数双积分的数值方法。
使用信赖域方法(Levenberg-Marquardt 方法的一种变体)的非线性最小二乘法最小化。
通过非线性最小二乘法拟合曲线和曲面。
用 Runge-Kutta 方法求解一阶初值微分方程的类。
与 .NET 标准库集成
使用标准 .NET 机制的完全持久数据类。
与 ADO.NET 集成。
NMath 统计功能总结
用于保存各种类型(数字、字符串、布尔值、日期时间和泛型)数据的数据框类,具有用于追加、插入、删除、排序和排列行和列的方法。
用于计算描述性统计的函数,例如平均值、方差、标准差、百分位数、中位数、四分位数、几何平均值、调和平均值、RMS、峰度、偏度等等。
特殊函数,例如阶乘、对数阶乘、二项式系数、对数二项式、对数伽马、不完全伽马、β 和不完全β。
各种概率分布的概率密度函数 (PDF)、累积分布函数 (CDF)、逆 CDF 和随机变量矩,包括 beta、二项式、卡方、指数、F、伽马、几何、逻辑、对数正态分布、负二项式、正态(高斯)、泊松、学生 t、三角和 Weibull 分布。
多元线性回归。
基本假设检验,例如 z 检验、t 检验和 F 检验,以及 p 值、临界值和置信区间的计算。
单向和双向方差分析(ANOVA) 以及重复测量方差分析 (RANOVA)。
非参数检验,例如 Kolmogorov-Smirnov 检验和 Kruskal-Wallis 秩和检验。
多元统计分析,包括主成分分析、因子分析、层次聚类分析和k均值聚类分析。
非负矩阵分解 (NMF),以及使用 NMF 的数据聚类。
偏最小二乘法 (PLS),包括交叉验证以及 SIMPLS 和 NIPALS 算法。
数据过滤,包括移动平均滤波器和 Savitzky-Golay 平滑滤波器。