线段树算法（C++/C）

news2024/11/16 5:57:43

目录​​​​​​​

一、线段树算法的概念

二、为什么需要线段树

三、线段树算法的实现

（1）建树

（2）查询

（3）修改

（4）综合代码，求区间和

（5）综合代码，求区间最大值

四、Lazy标记

一、线段树算法的概念

线段树（Segment Tree）是一种基于二分思想的数据结构，常常用于处理区间查询和区间修改。线段树的常用操作包括建树、查询、修改。

线段树的建树过程可以使用递归实现，也可以使用非递归实现（通常使用栈来实现）。

线段树的查询和修改基本都是从根节点开始，往下遍历到叶子节点或者与查询区间（或修改区间）不相交的节点为止。线段树相关问题经常需要使用懒惰标记（Lazy Tag）来优化。

线段树常用于以下场景：区间最值查询、区间求和、区间修改等

二、为什么需要线段树

考虑这样两个场景:

  1. 对于一个长度为 n 的数组,现在给定 l,r 让你求 l 到 r 所有元素的和,有多个这样的询问.
  2. 对于一个长度为 n 的数组，现在对数组的第 k 个元素进行修改后,给定 l,r 让你求 l 到 r 所有元素的和,有多个这样的询问.

大家看到第一种情况的时候,这不就是前缀和,是的.第二种情况呢,前缀和还能不能用,显然每次修改之后,前缀和就不能使用了,所以又退化为 O(n) 的时间复杂度了.

此时我们就需要用到我们的线段树了.

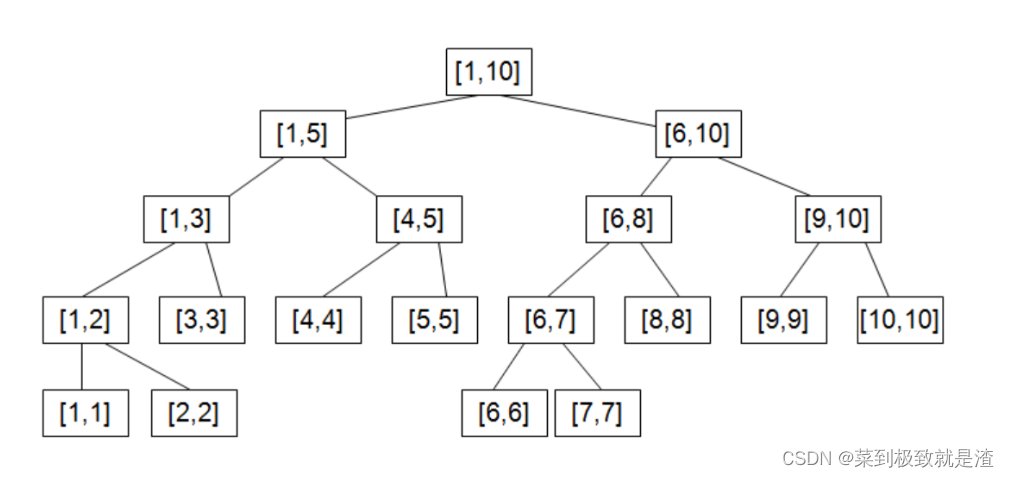
对于线段树中的每一个非叶子节点[a,b]，它的左儿子表示的区间为[a,(a+b)/2]，右儿子表示的区间为[(a+b)/2+1,b]。最后的子节点数目为 N，即整个线段区间的长度。

我们看一下 1-10 的线段树是如何存储的.

三、线段树算法的实现

（1）建树

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 节点p代表区间[l,r]
    if (l == r) { t[p].dat = a[l]; return; } // 叶节点
    int mid = (l + r) / 2; // 折半
    build(p*2, l, mid); // 左子节点[l,mid]，编号p*2
    build(p*2+1, mid+1, r); // 右子节点[mid+1,r]，编号p*2+1
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上传递信息
    t[p].dat = t[p*2].dat+t[p*2+1].dat; // 从下往上传递信息
}

（2）查询

int ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含，直接返回
    int mid = (t[p].l + t[p].r) / 2;
    int val = 0;
    if (l <= mid) val = val+ ask(p*2, l, r); // 左子节点有重叠
    if (r > mid) val = val+ask(p*2+1, l, r); // 右子节点有重叠
    return val;
}

（3）修改

void change(int p, int x, int v) {
    if (t[p].l == t[p].r) { t[p].dat = v; return; } // 找到叶节点
    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p*2, x, v); // x属于左半区间
    else change(p*2+1, x, v); // x属于右半区间
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上更新信息
    t[p].dat = t[p*2].dat+t[p*2+1].dat;
}

（4）综合代码，求区间和

#include<bits/stdc++.h>
using namespace std;

const int SIZE=11;

int a[11]={0,1,2,3,4,5,6,7,8,9,10}; //原始数据

struct SegmentTree {
    int l, r;
    int dat;
} t[SIZE * 4]; // struct数组存储线段树

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 节点p代表区间[l,r]
    if (l == r) { t[p].dat = a[l]; return; } // 叶节点
    int mid = (l + r) / 2; // 折半
    build(p*2, l, mid); // 左子节点[l,mid]，编号p*2
    build(p*2+1, mid+1, r); // 右子节点[mid+1,r]，编号p*2+1
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上传递信息
    t[p].dat = t[p*2].dat+t[p*2+1].dat; // 从下往上传递信息
}

void change(int p, int x, int v) {
    if (t[p].l == t[p].r) { t[p].dat = v; return; } // 找到叶节点
    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p*2, x, v); // x属于左半区间
    else change(p*2+1, x, v); // x属于右半区间
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上更新信息
    t[p].dat = t[p*2].dat+t[p*2+1].dat;
}

int ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含，直接返回
    int mid = (t[p].l + t[p].r) / 2;
    int val = 0;
    if (l <= mid) val = val+ ask(p*2, l, r); // 左子节点有重叠
    if (r > mid) val = val+ask(p*2+1, l, r); // 右子节点有重叠
    return val;
}
int main()
{
    //建树从根节点一点一点往下建立，所以第一个参数就是1号编号
    build(1,1,10);
    //查询区间[4,7]的和，第一个参数是1的原因是查询要从根节点开始递归
    int ans=ask(1,4,7);
    cout<<ans;
    //修改位置4的值变为25，第一个参数是1的原因是修改也要从根节点开始一步一步往下进行修改
    change(1,4,25);
    ans=ask(1,4,7);
    cout<<ans;
    return 0;

}

（5）综合代码，求区间最大值

#include<bits/stdc++.h>
using namespace std;

const int SIZE=11;

int a[11]={0,1,2,3,4,5,6,7,8,9,10}; //原始数据

struct SegmentTree {
    int l, r;
    int dat;
} t[SIZE * 4]; // struct数组存储线段树

void build(int p, int l, int r) {
    t[p].l = l, t[p].r = r; // 节点p代表区间[l,r]
    if (l == r) { t[p].dat = a[l]; return; } // 叶节点
    int mid = (l + r) / 2; // 折半
    build(p*2, l, mid); // 左子节点[l,mid]，编号p*2
    build(p*2+1, mid+1, r); // 右子节点[mid+1,r]，编号p*2+1
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上传递信息
    t[p].dat = max( t[p * 2].dat , t[p * 2 + 1].dat); // 从下往上传递信息
}

void change(int p, int x, int v) {
    if (t[p].l == t[p].r) { t[p].dat = v; return; } // 找到叶节点
    int mid = (t[p].l + t[p].r) / 2;
    if (x <= mid) change(p*2, x, v); // x属于左半区间
    else change(p*2+1, x, v); // x属于右半区间
    // t[p].dat = max(t[p*2].dat, t[p*2+1].dat); // 从下往上更新信息
    t[p].dat = max( t[p * 2].dat , t[p * 2 + 1].dat);
}

int ask(int p, int l, int r) {
    if (l <= t[p].l && r >= t[p].r) return t[p].dat; // 完全包含，直接返回
    int mid = (t[p].l + t[p].r) / 2;
    int val = 0;
    if (l <= mid) val = max(val, ask(p * 2, l, r)); // 左子节点有重叠
    if (r > mid) val =  max(val, ask(p * 2 + 1, l, r)); // 右子节点有重叠
    return val;
}
int main()
{
    build(1,1,10);
    int ans=ask(1,4,7);
    cout<<ans;
    change(1,4,25);
    ans=ask(1,4,7);
    cout<<ans;
    return 0;

}

四、Lazy标记

这种类型的题目，一般都是这样问的：如果每次是对一个区间进行修改,比如让 l,r 区间内的每个值都加 30.然后求和。

如果我们换成对于点的修改,那么时间复杂就太高了.那我们怎么办呢?

我们可以使用 Lazy 标记的方式,进行处理,什么是 Lazy 标记?

若在一次修改操作中发现节点 p 所代表的区间 [pl​,pr​] 被修改区间 [l,r] 完全覆盖，并且随后的查询操作没有利用到范围 [l,r] 的子区间作为候选答案，那么对节点 p 及其子树进行的更新操作将是没有实际效果的。此情况下，我们需要考虑优化算法，避免对整棵子树进行无意义的更新。

在执行修改指令时，如果发现存在 l < pl​ < pr​ < r 的情况，可以立即返回，并在回溯之前向节点 p 添加一个 Lazy 标记，用于表示 '该节点曾被修改，但其子节点尚未被更新'。

在后续的指令中，若需要向下递归至节点 p，应检查节点 p 是否带有标记。如果存在标记，应根据标记信息更新节点 p 的两个子节点，并为这两个子节点添加标记。然后清除节点 p 的标记。

除了在修改指令中直接划分成的 O(logN) 个节点外，对任意节点的修改都延迟到 '在后续操作中递归进入它的父节点时' 再执行。这样一来，每条查询或修改指令的时间复杂度都降低到了 O(logN)。我们将这些标记称为 '延迟标记'，它们提供了线段树中从上往下传递信息的方式。通过延迟标记的设计，我们能够更加高效地处理线段树操作。

这种 '延迟' 的思想是设计算法与解决问题时的一个重要思路，它充分利用了操作的特性，避免了不必要的计算，并提升了算法的效率。延迟标记的应用为线段树操作提供了一种优化策略，使得算法的时间复杂度得以降低。

那我们该如何设计呢.

#include <bits/stdc++.h>
using namespace std;

const int SIZE = 11;

int a[11] = {0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10}; // 原始数据

struct SegmentTree
{
    int l, r;
    long long sum, add;
} tree[SIZE * 4]; // struct数组存储线段树

void build(int p, int l, int r)
{
    tree[p].l = l, tree[p].r = r;
    if (l == r)
    {
        tree[p].sum = a[l];
        return;
    }
    int mid = (l + r) / 2;
    build(p * 2, l, mid);          // 构建左子树
    build(p * 2 + 1, mid + 1, r);  // 构建右子树
    tree[p].sum = tree[p * 2].sum + tree[p * 2 + 1].sum;  // 更新节点的区间和
}

void spread(int p)
{
    // 下传延迟标记
    if (tree[p].add)
    {
        tree[p * 2].sum += tree[p].add * (tree[p * 2].r - tree[p * 2].l + 1);
        tree[p * 2 + 1].sum += tree[p].add * (tree[p * 2 + 1].r - tree[p * 2 + 1].l + 1);
        tree[p * 2].add += tree[p].add;     // 左子树打延迟标记
        tree[p * 2 + 1].add += tree[p].add; // 右子树打延迟标记
        tree[p].add = 0;                    // 清除延迟标记
    }
}

void change(int p, int l, int r, int d)
{
    if (l <= tree[p].l && r >= tree[p].r)
    {
        // 完全覆盖节点的区间
        tree[p].sum = (long long)d * (tree[p].r - tree[p].l + 1);  // 更新节点的区间和
        tree[p].add += d;                                         // 打延迟标记
        return;
    }
    spread(p);
    int mid = (tree[p].l + tree[p].r) / 2;
    if (l <= mid)
        change(p * 2, l, r, d);         // 修改左子树
    if (r > mid)
        change(p * 2 + 1, l, r, d);     // 修改右子树
    tree[p].sum = tree[p * 2].sum + tree[p * 2 + 1].sum;  // 更新节点的区间和
}

long long ask(int p, int l, int r)
{
    if (l <= tree[p].l && r >= tree[p].r)
        return tree[p].sum;
    spread(p);
    int mid = (tree[p].l + tree[p].r) / 2;
    long long val = 0;
    if (l <= mid)
        val += ask(p * 2, l, r);          // 查询左子树
    if (r > mid)
        val += ask(p * 2 + 1, l, r);      // 查询右子树
    return val;
}

int main()
{
    build(1, 1, 10);
    int ans = ask(1, 4, 7);
    cout << ans << endl;
    change(1, 4, 5, 10);
    ans = ask(1, 4, 7);
    cout << ans << endl;
    return 0;
}

 

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/605406.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

从“互联网+”到“互联网医疗+”，免费互联网医院开创新格局

从“互联网+”到“互联网医疗+”，免费互联网医院开创新格局

随着互联网的发展&#xff0c;各行各业都在积极探索“互联网”时代下的创新模式。其中&#xff0c;医疗领域也开始了自己的变革之路&#xff0c;从传统的医疗模式转向了“互联网医疗”的新型格局。免费互联网医院的出现&#xff0c;则更是为这一变革注入了新的活力。 所谓“互联…
阅读更多...
【嵌入式系统应用开发】FPGA——基于HC-SR04超声波测距

【嵌入式系统应用开发】FPGA——基于HC-SR04超声波测距

文章目录 前言环境目标结果 1 实验原理1.1 超声波原理1.2 硬件模块时序图1.3 模块说明 2 设计文件2.1 时钟分频2.2 超声波测距2.3 超声波驱动 3 实验验证3.1 编译3.3 硬件测试 总结 前言 环境 硬件 DE2-115 HC-SR04超声波传感器软件 Quartus 18.1 目标结果 使用DE2-115开发…
阅读更多...
【Linux驱动】认识驱动（驱动的概念、驱动分类）

【Linux驱动】认识驱动（驱动的概念、驱动分类）

目录 1、什么是驱动&#xff1f; 2、应用程序调用驱动基本流程 3、file_operations 结构体 4、驱动的分类 1、什么是驱动&#xff1f; 驱动就是一段程序&#xff0c;能够获取外设或者传感器数据、控制外设。驱动获取到的数据会提交给应用程序。 在 Linux 中一切皆为文件&…
阅读更多...
【实用篇】Elasticsearch02

【实用篇】Elasticsearch02

文章目录 分布式搜索引擎021.DSL查询文档1.1.DSL查询分类1.2.全文检索查询1.2.1.使用场景1.2.2.基本语法1.2.3.示例1.2.4.总结 1.3.精准查询1.3.1.term查询1.3.2.range查询1.3.3.总结 1.4.地理坐标查询1.4.1.矩形范围查询1.4.2.附近查询 1.5.复合查询1.5.1.相关性算分1.5.2.算分…
阅读更多...
Linux开机rc.local不自启动执行脚本问题的排查思路及问题解决

Linux开机rc.local不自启动执行脚本问题的排查思路及问题解决

Linux开机rc.local不自启动执行脚本问题的排查思路及问题解决 问题 Linux系统中&#xff0c;在rc.local里面配置的启动命令等不能能够在开机的时候进行自启动 问题解决 解决问题排查中最大的麻烦&#xff0c;需要进行reboot重启 查看rc-local的运行状态 systemctl status r…
阅读更多...
clickhouse简介与实战

clickhouse简介与实战

文章目录 1&#xff1a;简介1.1&#xff1a;CH是什么&#xff1f;1.2&#xff1a;CH优缺点1.2.1&#xff1a;优势1.2.2&#xff1a;缺点 1.3&#xff1a;架构设计 2&#xff1a;CH接口3&#xff1a;CH引擎1&#xff1a;数据库引擎3.1.1:mysql引擎 2&#xff1a;表引擎3.2.1&…
阅读更多...
路径规划算法：基于模拟退火优化的路径规划算法- 附代码

路径规划算法：基于模拟退火优化的路径规划算法- 附代码

路径规划算法&#xff1a;基于模拟退火优化的路径规划算法- 附代码 文章目录 路径规划算法&#xff1a;基于模拟退火优化的路径规划算法- 附代码1.算法原理1.1 环境设定1.2 约束条件1.3 适应度函数 2.算法结果3.MATLAB代码4.参考文献 摘要&#xff1a;本文主要介绍利用智能优化…
阅读更多...
基于flask的web应用开发——访问漂亮的html页面以及页面跳转

基于flask的web应用开发——访问漂亮的html页面以及页面跳转

目录 0. 前言1. html基本知识2. 编写html文本3. 在Flask中设置访问html4. 实现点击跳转 0. 前言 本节学习如何在flask应用程序下让用户访问你提前制作好的html页面 操作系统&#xff1a;Windows10 专业版 开发环境&#xff1a;Pycahrm Comunity 2022.3 Python解释器版本&am…
阅读更多...
（学习日记）2023.04.27

（学习日记）2023.04.27

写在前面&#xff1a; 由于时间的不足与学习的碎片化&#xff0c;写博客变得有些奢侈。 但是对于记录学习&#xff08;忘了以后能快速复习&#xff09;的渴望一天天变得强烈。 既然如此 不如以天为单位&#xff0c;以时间为顺序&#xff0c;仅仅将博客当做一个知识学习的目录&a…
阅读更多...
防火墙之IPSec VPN实验

防火墙之IPSec VPN实验

防火墙IPSec VPN实验 原理概述: 指采用IPSec协议来实现远程接入的一种VPN技术&#xff0c;IPSec全称为Internet Protocol Security&#xff0c;是由Internet Engineering Task Force (IETF) 定义的安全标准框架&#xff0c;在公网上为两个私有网络提供安全通信通道,通过加密通道…
阅读更多...
【数据结构】单调栈

【数据结构】单调栈

目录 1.概述2.代码框架2.1.单调递增栈2.2.单调递减栈 3.应用3.1.应用一3.2.应用二 1.概述 &#xff08;1&#xff09;单调栈是一种特殊的栈&#xff0c;它在普通栈的基础上要求从栈顶到栈底的元素是单调的&#xff0c;如果栈中的元素从栈顶到栈底是单调递增的&#xff0c;那么…
阅读更多...
Linux CGroup 原理

Linux CGroup 原理

Linux CGroup 原理 1、CGroup简介 cgroups是Linux下控制一个&#xff08;或一组&#xff09;进程的资源限制机制&#xff0c;全称是control groups&#xff0c;可以对cpu、内存等资源做精细化控制。 开发者可以直接基于cgroups来进行进程资源控制&#xff0c;比如8核的机器上…
阅读更多...
JAVA用tess4j识别复杂的验证码，自定义字库，计算题验证码，jTessBoxEditor，tess4j，验证码识别

JAVA用tess4j识别复杂的验证码，自定义字库，计算题验证码，jTessBoxEditor，tess4j，验证码识别

JAVA用tess4j识别复杂的验证码&#xff0c;自定义字库&#xff0c;计算题验证码 场景JAVA用tess4j识别文本MAVEN依赖traineddata文件下载识别英文识别中文 JAVA用tess4j识别验证码常见验证码的类型识别 自定义字库&#xff0c;提高识别率下载jTessBoxEditor解压运行准备素材合并…
阅读更多...
微信小程序入门笔记

微信小程序入门笔记

常用技术&#xff1a;开源库 图表&#xff1a;wxcharts-min.js 网络通信&#xff1a;类似 ajax ui: WeUi JSON 配置文件 小程序中&#xff0c;包含唯一的全局配置文件 app.json&#xff0c;以及每个页面的配置文件 page.json。每单页页面相应的 JSON 文件会覆盖与 app.json相同…
阅读更多...
门控时钟检查（clock gating check）的理解和设计应用（上）

门控时钟检查（clock gating check）的理解和设计应用（上）

在笔者的一篇老文Clock Gating之浅见 中&#xff0c;一起探讨过工具处理门控时钟的方法和门控时钟所带来的相关收益和面积代价。除此之外&#xff0c;门控时钟的检查&#xff08;clock-gating check&#xff09;在STA中也有相应的处理方式&#xff0c;通过这篇文章&#xff0c;…
阅读更多...
4年测试经验，一问三不知，过于离谱...

4年测试经验，一问三不知，过于离谱...

公司今年要招人&#xff0c;面倒是面了很多测试&#xff0c;但没有一个合适的。一开始想要的就是中级的水准&#xff0c;也没指望来大牛&#xff0c;当然来了更好&#xff0c;提供的薪资在10-20k,来面试的人有很多&#xff0c;但平均水准真的是让人失望。 看简历时很多都写着3…
阅读更多...
【瑞萨MCU】玩转 HMI-Board 之 MDK + RASC 点灯

【瑞萨MCU】玩转 HMI-Board 之 MDK + RASC 点灯

此前我们已经配置好了 瑞萨 MCU MDK RASC 的开发环境&#xff0c;接下来进入到瑞萨 MCU 的 HelloWorld 环节&#xff0c;使用 MDK 点亮两个 LED 灯。 这次我们使用的是瑞萨和 RT-Thread 联合推出的 HMI-Board 开发板。 HMI-Board 开发板简介 HMI-Board 为 RT-Thread 联合瑞…
阅读更多...
3.6 多边形游戏

3.6 多边形游戏

博主简介&#xff1a;一个爱打游戏的计算机专业学生博主主页&#xff1a; 夏驰和徐策所属专栏&#xff1a;算法设计与分析 1.什么是多边形游戏&#xff1f; 对于多边形游戏&#xff0c;一种特定类型的玩法&#xff0c;即在给定的简单多边形上进行移动、删除顶点或边&#xff…
阅读更多...
[图表]pyecharts-3D柱状图

[图表]pyecharts-3D柱状图

[图表]pyecharts-3D柱状图 先来看代码&#xff1a; import randomfrom pyecharts import options as opts from pyecharts.charts import Bar3D from pyecharts.faker import Fakerdata [(i, j, random.randint(0, 12)) for i in range(6) for j in range(24)] c (Bar3D().…
阅读更多...
box-shadow盒子阴影几种用法

box-shadow盒子阴影几种用法

box-shadow盒子阴影 语法&#xff1a; 外阴影&#xff1a;box-shadow: X轴 Y轴 Rpx color; 属性说明&#xff08;顺序依次对应&#xff09;&#xff1a; 阴影的X轴(可以使用负值) 阴影的Y轴(可以使用负值) 阴影模糊值&#xff08;大小&#xff09; 阴影的颜色 内阴…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023