文章目录
- A. Grasshopper on a Line
- 1、问题
- 2、分析
- 3、代码
- B. Comparison String
- 1、问题
- 2、分析
- 3、代码
- C. Best Binary String
- 1、问题
- 2、分析
- 3、代码
- D. Bracket Coloring
- 1、问题
- 2、分析
- 3、代码
- E. Playoff Fixing
- 1、问题
- 2、分析
- 3、代码
- F. Editorial for Two
- 1、问题
- 2、分析
- 3、代码
A. Grasshopper on a Line
A. Grasshopper on a Line
1、问题
给定一个 n n n和 k k k, n n n可以写作 m m m个数字的和,但是题目规定这些数字不能是 k k k的倍数。现在需要我们找最小的 m m m,同时输出这 m m m个数字。
2、分析
如果 n n n不是 k k k的倍数,这里可以直接输出 n n n,即 m = 1 m=1 m=1。
如果 n n n是 k k k的倍数,说明我们需要将 n n n进行拆分。这里给定一个结论:对于该种情况下的任意数字 n n n,都只需要拆成两个数字。
证明:
因为
n
n
n是
k
k
k的倍数,我们可以假设
n
=
a
∗
k
n=a*k
n=a∗k。
如果 a ≥ 2 a\geq 2 a≥2
那么我们可以令 p + q = a p+q=a p+q=a,则 n = ( p + q ) ∗ k = p ∗ k + q ∗ k n=(p+q)*k=p*k+q*k n=(p+q)∗k=p∗k+q∗k,此时我们可以让 a n s 1 = p ∗ k + 1 ans_1=p*k+1 ans1=p∗k+1, a n s 2 = q ∗ k − 1 ans_2=q*k-1 ans2=q∗k−1,因为题目规定 k ≥ 2 k \geq 2 k≥2。所以构造后的 p p p和 q q q都不会是 k k k的倍数。
如果 a < 2 a < 2 a<2,即 a = 1 a=1 a=1,此时可以让 p = 1 , q = n − 1 p=1,q=n-1 p=1,q=n−1即可。
3、代码
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n, k;
cin >> n >> k;
if(n % k != 0)
{
cout << 1 << endl;
cout << n << endl;
}
else
{
cout << 2 << endl;
int a = n / k;
if(a == 1)
cout << 1 << " " << n - 1 << endl;
else
cout << (a - 1) * k + 1 << " " << k - 1 << endl;
}
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
B. Comparison String
B. Comparison String
1、问题
给定一个由 ′ < ′ '<' ′<′和 ′ > ′ '>' ′>′构成的字符串S,其中如果S[i]表示 ‘ > ‘ ‘>‘ ‘>‘,则对应的a数组则需要满足: a [ i ] > a [ i + 1 ] a[i]>a[i+1] a[i]>a[i+1],现在请用最少的数字构造出a数组,输出不同数字的个数。
2、分析

根据上面的例子可以看出,如果’>‘或者’<'连续排列的时候,我们的元素个数就会递增。当出现与之相反的符号的时候,我们可以用刚刚出现的数字构造出来。
而通过上述样例不难发现这样一个规律。
'>‘和’<'分别对应一个最长的连续子串,长度分别记为
p
p
p和
q
q
q。那么答案就是:
a
n
s
=
m
a
x
(
p
,
q
)
+
1
ans=max(p,q)+1
ans=max(p,q)+1。
3、代码
#include<bits/stdc++.h>
using namespace std;
void solve()
{
int n;
string s;
cin >> n >> s;
int ans = 0;
for(int i = 0; i < n; i ++)
{
int j = i;
while(j < n && s[j] == s[i])
j ++;
ans = max(ans, j - i);
i = j - 1;
}
cout << ans + 1 << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
C. Best Binary String
C. Best Binary String
1、问题
给定一个字符串,这个字符串是由1,0,?三个字符构成的,其中?部分我们可以填写0也可以填写1,每个?之间是独立的,即某个?的填写并不影响后续?的填写选择。现在我们需要给字符串中的每一个?赋值。得到一个 01 01 01串,那么对于该 01 01 01串可以进行如下操作:选择任意连续子串进行反转。多次操作后,可以将该字符串排列为一个非降序字符串。在这个过程中,会得到一个操作次数。现在我们需要输出一个最小操作次数的 01 01 01字符串。
2、分析
按照题目要求,经过多次操作后,我们的字符串会变成下面的样子:

也就是说,我们需要将所有的1放在一起,所有的0放在一起。

从上面这个例子看出,只要有非连续的1存在,我们就需要一次操作,即存在多少个连续的1的字串,就需要进行几次反转,所以 我们的目的就是尽量减少连续1子串的个数。
从上面这个结论可以看出,只要是形如:“1???1” 的子串存在,中间的问号都需要写成数字1。
如果是**“0???1"或者"1???0”**的话,中间的问号都填0或者都填1其实是无所谓的。那么我们可以规定如果开头是0,就都写0,如果开头是1,就都写1。这样做的目的是为了好写代码。
如果问号出现在开头"???0",如果是这种情况,则需要全写0。因为如果我们全写1的话,会导致1的子串增多。
如果开头是"???1"全写0或者全写1都不影响1子串的个数,可以规定写0。这样的话,我们就可以将开头的情况统一一下:都写0。
如果问号出现在结尾:“1???”,全写1即可。
如果结尾是"0???"全写0即可。即开头是什么就写什么。
因此,上面的所有情况都可以归结为下面的方法:
如果开头是?,就改成0,剩余?都和前一个字符一致即可。(可以按照上述的分类讨论自行验证)
3、代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
void solve()
{
string s;
cin >> s;
if(s[0] == '?')
s[0] = '0';
for(int i = 0; i < s.size() - 1; i ++)
if(s[i + 1] == '?')
s[i + 1] = s[i];
cout << s << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
D. Bracket Coloring
D. Bracket Coloring
1、问题
给定一个括号序列,如果括号序列是能够匹配上的, 例如:“()()”,“(()())”,“((()))”,或者反转以后是能够匹配上的,例如:“)(”, “))((”,就叫做美丽的括号序列。
现在给我们随机的一个括号序列,我们需要给这个括号序列进行染色,相同颜色的括号需要组成一个美丽的括号序列。
现在需要我们输出需要的最少颜色以及染色的策略。如果不论怎么染色都无法构成美丽括号序列的话,就输出-1。
2、分析
因为括号要左右一一匹配,所以如果左括号的个数不等于右括号的个数,则不可能构造出来答案,直接输出-1。
如果左括号的个数等于右括号的个数,则一定可以构造出来。为什么呢?
对于任意1个左括号和右括号,“)(”,“()”,都是美丽的,所以最坏情况下,我们给每一对括号都染色,则就会出现 n 2 \frac{n}{2} 2n个美丽括号。所以一定有解。
在考虑完是否有解后,我们接下来考虑一下最优解如何构造。
这里还是先给出一个结论,再证明:颜色的个数要么是1个,要么是2个。
1个的情况很简单,如果输入的括号序列本身就是美丽的,则只需要染成1个颜色。
接下来看一下2个颜色的情况:

如果是上图的情况,则最少是两种颜色,无可厚非。

如果是左图的情况,可以将后面红色的括号统一为前面蓝色的括号。其余情况同理。
接下来的问题就是涂色的问题了。
对于括号匹配的问题,通常用栈来解决。我们将第一个括号放到栈里,如果出现和第一个括号相同的括号就放到栈里,如果出现与之匹配的括号,就从栈顶取出一个括号与之匹配,然后删除栈顶。
如果遇到了能够和栈中括号匹配的括号,但栈却为空,说明需要涂成另外一个颜色。最后栈中剩下的括号,也需要涂成另外的颜色。
3、代码
#include<bits/stdc++.h>
#define endl '\n'
using namespace std;
void solve()
{
int n;
string s;
cin >> n >> s;
int nums = 0;
for(int i = 0; i < n; i ++)
if(s[i] == '(')
nums ++;
if(2 * nums != n)
{
cout << -1 << endl;
return;
}
string str = "";
for(int i = n - 1; i >=0; i --)
str.push_back(s[i]);
vector<int>ans(n, 0);
stack<pair<char,int>>stk1;
for(int i = 0; i < n; i ++)
{
if(s[i] == s[0])
stk1.push({s[i], i});
else
{
if(stk1.empty())
ans[i] = 2;
else
{
auto t = stk1.top();
stk1.pop();
ans[t.second] = 1;
ans[i] = 1;
}
}
}
while(stk1.size())
{
auto t = stk1.top();
stk1.pop();
ans[t.second] = 2;
}
int x = 0;
for(int i = 0; i < n; i ++)
x += ans[i];
if(x == n || x == 2 * n)
{
cout << 1 << endl;
for(int i = 0; i < n; i ++)
cout << 1 << " ";
cout << endl;
return;
}
cout << 2 << endl;
for(auto x : ans)
cout << x << " ";
cout << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}
E. Playoff Fixing
E. Playoff Fixing
1、问题
2、分析
3、代码
F. Editorial for Two
F. Editorial for Two
1、问题
给定一个 n n n和 k k k,以及一个长度为 n n n数组。现在从 n n n个数中,挑出 k k k个数,称作个子序列。然后将这个子序列分成两部分,记作子序列1和子序列2。那么子序列1和子序列2都有一个对应的和。这两个和能够比较出一个最大值。现在我们要求的是最大值的最小值。
2、分析
这里有一个很常用的套路,当题目中让我们求最大值的最小值或者最小值的最大值的时候,一般采用二分来解决。
我们这里二分最终的答案。
对于二分而言,难点在于 c h e c k check check函数的书写。
这道题中, c h e c k check check函数的作用是判断二分过程中的 m i d mid mid值是否合理。
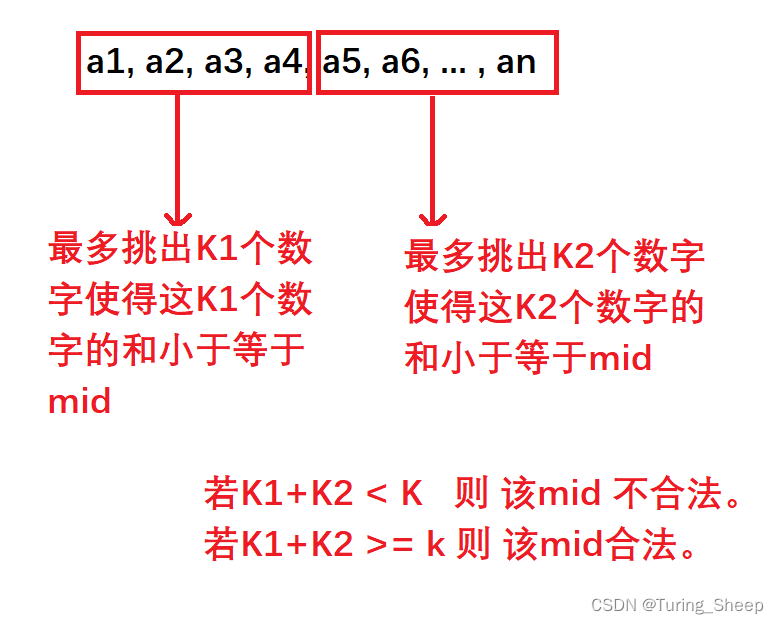
那么这个挑出最多
k
1
k1
k1个数的过程,用到了反悔贪心,反悔贪心的思路就是当所选数字的和小于
m
i
d
mid
mid的时候,就尽可能多的选数字,当大于
m
i
d
mid
mid的时候,就删除选择数字中的最大值,目的是留出更大空间选择更多的数字,而这个选择最大值的过程可以用大根堆来优化。
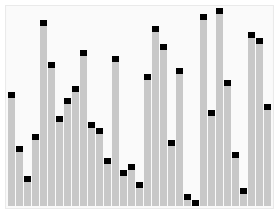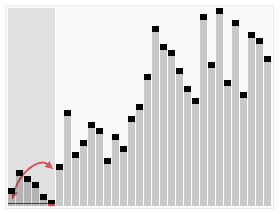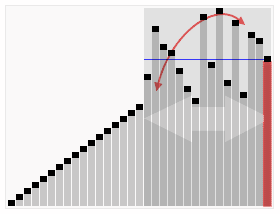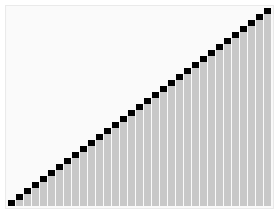
除此以外,图中前缀后缀划分的位置是不确定的,所以我们需要枚举所有的划分位置,找到一个可行的方案。
因此,我们可以先利用反悔贪心先预处理出来所有的前缀后缀中最多选择的数字 k 1 , k 2 k1,k2 k1,k2。然后再枚举划分位置,判断是否存在一组 k 1 + k 2 ≥ k k1+k2 \geq k k1+k2≥k。
复杂度为: O ( l o g ( s u m ) ∗ ( n l o g n + n ) ) = O ( l o g ( s u m ) n l o g n ) O(log(sum)*(nlogn+n))=O(log(sum)\ n\ logn) O(log(sum)∗(nlogn+n))=O(log(sum) n logn)
3、代码
#include<bits/stdc++.h>
#define endl '\n'
#define int long long
using namespace std;
bool check(int maxv, int n, vector<int>a, int k)
{
vector<int>f(n + 1, 0), g(n + 1, 0);
priority_queue<int>q, qq;
int sum = 0;
for(int i = 0; i < n; i ++)
{
if(sum + a[i] <= maxv)
{
sum += a[i];
q.push(a[i]);
f[i + 1] = f[i] + 1;
}
else
{
q.push(a[i]);
sum += a[i];
sum -= q.top();
q.pop();
f[i + 1] = f[i];
}
}
sum = 0;
reverse(a.begin(), a.end());
for(int i = 0; i < n; i ++)
{
if(sum + a[i] <= maxv)
{
sum += a[i];
qq.push(a[i]);
g[i + 1] = g[i] + 1;
}
else
{
sum += a[i];
qq.push(a[i]);
sum -= qq.top();
qq.pop();
g[i + 1] = g[i];
}
}
for(int i = 1; i <= n; i ++ )
{
if(f[i] + g[n - i] >= k)
return true;
}
return false;
}
void solve()
{
int n, k;
cin >> n >> k;
vector<int>a(n);
int sum = 0;
for(int i = 0; i < n; i ++)
{
cin >> a[i];
sum += a[i];
}
int l = 0, r = sum;
while(l < r)
{
int mid = l + r >> 1;
if(check(mid, n, a, k))
r = mid;
else
l = mid + 1;
}
cout << l << endl;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);
cout.tie(0);
int t;
cin >> t;
while(t--)
solve();
}