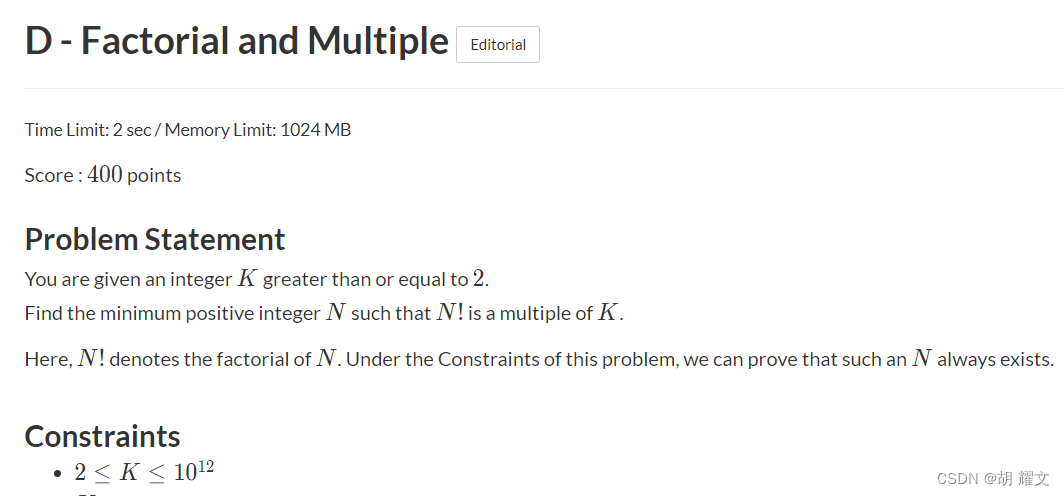
解法1，直接暴力，答案一定在2~1e6里面或者k本身（如果k是个质数的话）

#include<bits/stdc++.h>
using namespace std;
signed main() {
	long long k;
	cin>>k;
	for(long long i=1;i<=2000010;i++) {
		k/=__gcd(k,i);
		if(k==1) {
			cout<<i<<endl;
			return 0;
		}
	}
	cout<<k<<endl;
	return 0;
}

解法2，质因数分解，对每个质因数$$a^b$$
$$找到右边界R,ans=max(ans,R)$$

#include<bits/stdc++.h>
#define int long long
using namespace std;
int n,m,a[11];
int sum(int i,int j){
    int ans=0;
    while(j%i==0)j/=i,ans++;
    return ans;
}
int cal(int i,int cnt){
    for(int j=1;;j++){
        cnt-=sum(i,j*i);
        if(cnt<=0)return i*j;
    }
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    cin>>n;
    int ma=2;
    for(int i=2;i*i<=n;i++){
        if(n%i==0){
            int cnt=0;
            while(n%i==0)n/=i,cnt++;
            ma=max(ma,cal(i,cnt));
        }
    }
    if(n>1)ma=max(ma,n);
    cout<<ma;
}

这道题就不能像上面那样暴力做了，要二分

class Solution {
public:
    long long sum(int x){
        long long ans=0;
        //相当于有多少个是5的倍数，有多少个是25的倍数，有多少个是125的倍数....
        while(x){
            ans+=x/5;
            x/=5;
        }
        return ans;
    }
    long long cal(long long k){
        long long r=k*5;
        long long l=0;
        while(l<r){
            long long mid=l+r>>1;
            if(sum(mid)>=k)r=mid;//找到最左的一个数字x，满足sum(x)大于等于k
            else l=mid+1;
        }
        return r;
    }
    int preimageSizeFZF(int k) {
        return cal(k+1)-cal(k);
    }
};

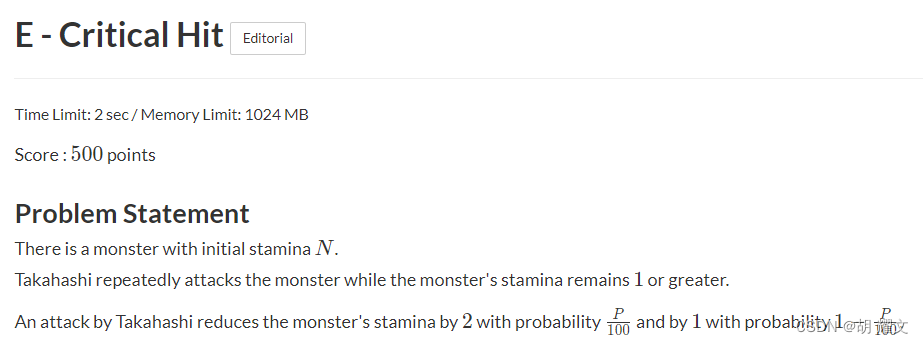
记住当初的错误做法以及为什么错了

#include<bits/stdc++.h>
#define int long long
using namespace std;
int mod=998244353;
int n,p,t,ans,A,B;
const int N=2e5+10;
int fac[N],inv[N];
int qpow(int a,int b){
    int ans=1;
    while(b){
        if(b&1)ans=ans*a%mod;
        b/=2;
        a=a*a%mod;
    }
    return ans;
}
int f[N];
int dfs(int x){
    if(x<=0)return 0;
    if(f[x])return f[x];
    return f[x]=(1+dfs(x-1)*A+dfs(x-2)*B)%mod;
    
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    t=qpow(100,mod-2);
    cin>>n>>p;
    A=(100-p)*t%mod;
    B=p*t%mod;
    cout<<dfs(n);
}

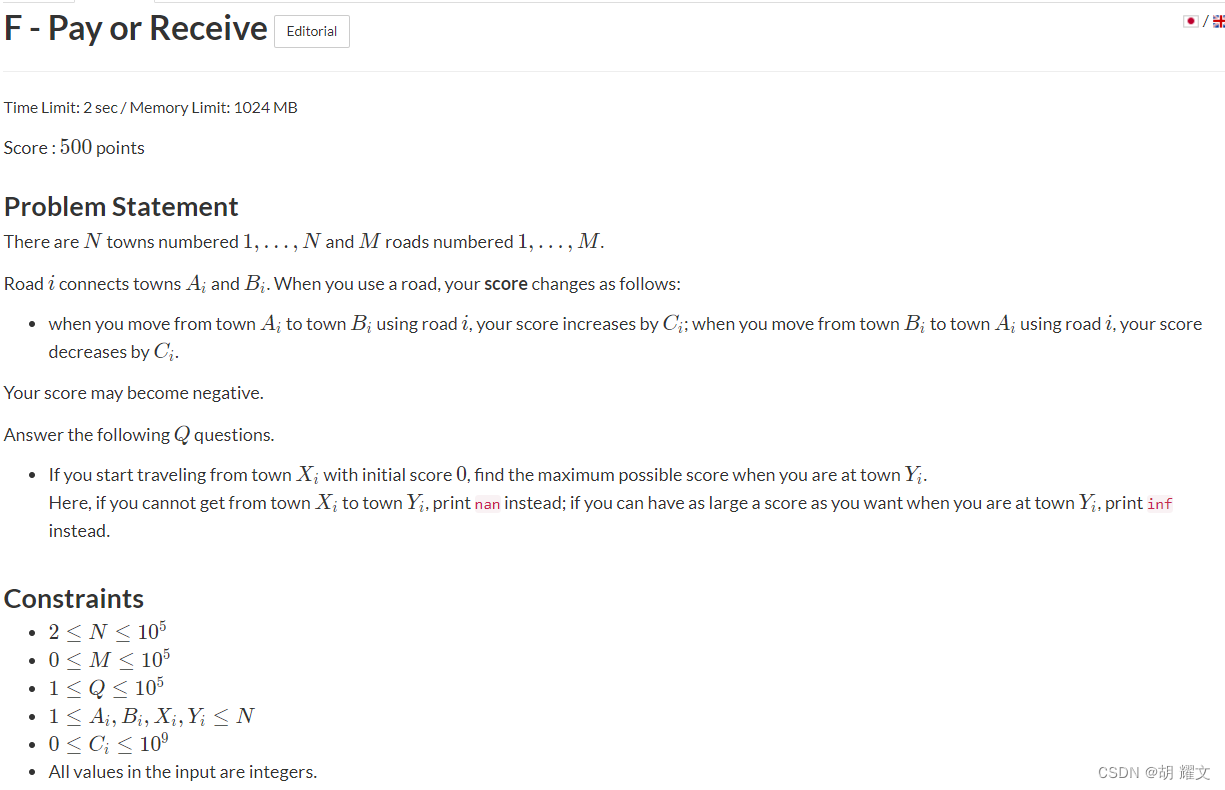
如果不在一个连通分量里面就是nan
如果在一个连通分量里面
$$这个连通分量存在正环->inf$$
$$这个连通分量不存在正环，两点之间距离=d[b]-d[a]$$

#include<bits/stdc++.h>
using namespace std;
#define int long long
const int N=2e5+10;
int n,m,q,a,b,c,rt[N],cir[N],f[N];
typedef pair<int,int>PII;
vector<PII>g[N];
void dfs(int u,int fa){
    rt[u]=fa;
    for(auto [j,w]:g[u]){
        if(rt[j]==fa&&f[j]!=f[u]+w)cir[fa]=1;
        if(rt[j]==0)f[j]=f[u]+w,dfs(j,fa);
        
    }
}
signed main(){
    ios::sync_with_stdio(0);cin.tie(0);
    cin>>n>>m>>q;
    while(m--){
        cin>>a>>b>>c;
        g[a].push_back({b,c});
        g[b].push_back({a,-c});
    }
    for(int i=1;i<=n;i++){
        if(!rt[i])dfs(i,i);
    }
    while(q--){
        cin>>a>>b;
        if(rt[a]!=rt[b]){cout<<"nan"<<'\n';continue;}
        if(cir[rt[a]])cout<<"inf"<<'\n';
        else cout<<f[b]-f[a]<<'\n';
    }
}