leetcode95 – 不同的二叉搜索树 II

原题链接:
https://leetcode.cn/problems/unique-binary-search-trees-ii/

题目描述

给你一个整数 n ，请你生成并返回所有由 n 个节点组成且节点值从 1 到 n 互不相同的不同二叉搜索树。可以按任意顺序返回答案。

示例1:

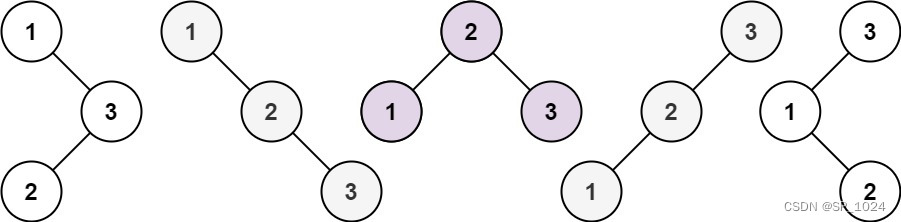
输入：n = 3
输出：[[1,null,2,null,3],[1,null,3,2],[2,1,3],[3,1,null,null,2],[3,2,null,1]]

示例2:
输入：n = 1
输出：[[1]]

提示：
1 <= n <= 8

解题思路

我们用递归去解答.
递归时首先选择不同的数字来当头节点,
选中头节点后,左树能选的数字只能比他小的.
右边子树能选的数字要比这个这个数字大
这样是为了满足搜索二叉树,.
这样递归下去,我们就可以得到左树能组成的所有可能
得到右树所有的可能
然后把两边的可能进行排列组合
组成一颗树,加到集合中,进行返回.

代码演示

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    public List<TreeNode> generateTrees(int n) {
        if(n == 1){
            List<TreeNode> ans = new ArrayList<>();
            ans.add(new TreeNode(n));
        }
        return process(1,n);
    }

	/**
	* 递归
	* L 左边界
	* R 右边界
	*/
    public List<TreeNode> process(int L ,int R){
        List<TreeNode> ans = new ArrayList<>();
        //base case 
        if(L > R){
            ans.add(null);
            return ans;
        }
        //从左边界到右边界依次选择一个数字当头节点
        for(int i = L ; i <= R;i++){
       		 // 左树所有的可能组合
       		 //因为是搜索二叉树,左边的节点的值要比头节点小,
       		 //选择一个数当头节点后,
       		 //左树可选数字只能是小于当前数字的
            List<TreeNode> lefts = process(L,i - 1);
            //右树边界 
            List<TreeNode> rights = process(i + 1,R);
            for(TreeNode left : lefts){
                for(TreeNode rig : rights){
                //排列组合 进行把左树所有的组合和右树所有的组合,
                //组成不同的树,加到集合中
                    TreeNode head = new TreeNode(i);
                    head.left = left;
                    head.right = rig;
                    ans.add(head);

                }
            }
        }
        return ans;

    }
}