84.柱状图中最大的矩形

教程视频：https://www.bilibili.com/video/BV1Ns4y1o7uB
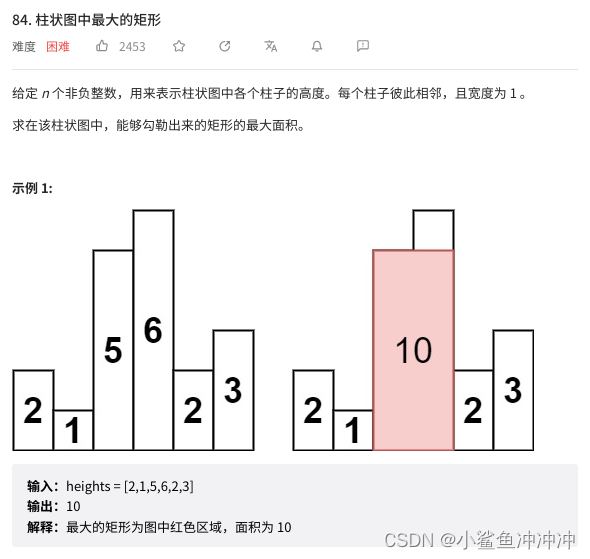
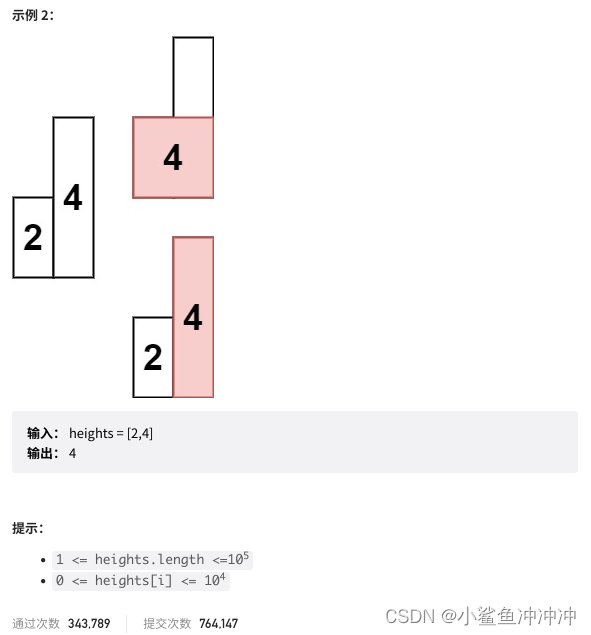
在这里插入图片描述

包含索引i中部分面积的最大矩形面积取决于该索引两侧第一个小于height[i]的值,以及这两个索引之间的距离。
因此本题需要找到索引两侧第一个小于height[i]的值，适合用单调栈来解决。

解法一：单调栈

因为本题是要找每个柱子左右两边第一个小于该柱子的柱子，从栈头（元素从栈头弹出）到栈底的顺序应该是从大到小的顺序！
栈顶决定了最大面积的高度，和栈顶的下一个元素以及要入栈的三个元素决定了最大面积的宽度。

分析清楚如下三种情况：
情况一：当前遍历的元素heights[i]大于栈顶元素heights[stack.peek()]的情况
情况二：当前遍历的元素heights[i]等于栈顶元素heights[stack.peek()]的情况
情况三：当前遍历的元素heights[i]小于栈顶元素heights[stack.peek()]的情况

【注意】
为了保证一定存在左边界，需要再数组开头加个0；
为了保证一定存在右边界，需要再数组末尾加个0，这样才能保证对每个数值都计算对应最大面积（即最后弹出所有元素）。

class Solution {
    public int largestRectangleArea(int[] heights) {
         // 数组扩容，在头和尾各加入一个元素0
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        int result = 0;
        Deque<Integer> stack = new LinkedList<>();
        stack.push(0);
        for(int i=1;i<newHeights.length;i++){
            if(newHeights[i]>newHeights[stack.peek()]){
                stack.push(i);
            }else if(newHeights[i]==newHeights[stack.peek()]){
                stack.pop();
                stack.push(i);
            }else{
                while(!stack.isEmpty() && newHeights[i]<newHeights[stack.peek()]){
                    int mid = stack.pop();
                    if(!stack.isEmpty()){
                        int left = stack.peek();
                        result = Math.max(result, newHeights[mid]*(i-left-1));
                    }
                }
                stack.push(i);
            }
        }
        return result;
    }
}

//精简版
class Solution {
    public int largestRectangleArea(int[] heights) {
        int[] newHeight = new int[heights.length + 2];
        System.arraycopy(heights, 0, newHeight, 1, heights.length);
        newHeight[heights.length+1] = 0;
        newHeight[0] = 0;

        Stack<Integer> stack = new Stack<>();
        stack.push(0);

        int res = 0;
        for (int i = 1; i < newHeight.length; i++) {
            while (newHeight[i] < newHeight[stack.peek()]) {
                int mid = stack.pop();
                int w = i - stack.peek() - 1;
                int h = newHeight[mid];
                res = Math.max(res, w * h);
            }
            stack.push(i);

        }
        return res;
    }
}

解法二：暴力双指针(会超时)

class Solution {
    public int largestRectangleArea(int[] heights) {
        int result=0;
         for(int i=0;i<heights.length;i++){
            int left=i-1;
            while(left>=0){
                if(heights[left]>heights[i])continue;
                left--;
            }
            if(left==-1)left=0;
            
            int right=i+1;
            while(right<heights.length){
                if(heights[right]>heights[i])continue;
                right++;
            }
            if(right==heights.length)right=heights.length-1;
            result=Math.max(result, (right-left-1)*heights[i]);
         }
         return result;
    }
}

解法三:优化双指针

class Solution {
    public int largestRectangleArea(int[] heights) {
        int length = heights.length;
        int[] leftMin = new int[length];
        int[] rightMin = new int[length];
        // 记录左边第一个小于该柱子的下标
        leftMin[0] = -1 ;
        for(int i=1;i<length;i++){
            int temp=i-1;
            while(temp>=0 && heights[temp]>=heights[i]){// 这里不断向左寻找的过程
                temp=leftMin[temp];
            }
            leftMin[i]=temp;
        }
        // 记录每个柱子右边第一个小于该柱子的下标
        rightMin[length-1]=length;
        for(int i=length-2;i>=0;i--){
            int temp=i+1;
            while(temp<length && heights[temp]>=heights[i]){// 这里不断向左寻找的过程
                temp=rightMin[temp];
            }
            rightMin[i]=temp;
        }
         // 求和
        int result = 0;
        for (int i = 0; i < length; i++) {
            int sum = heights[i] * (rightMin[i] - leftMin[i] - 1);
            result = Math.max(sum, result);
        }
        return result;
    }
}