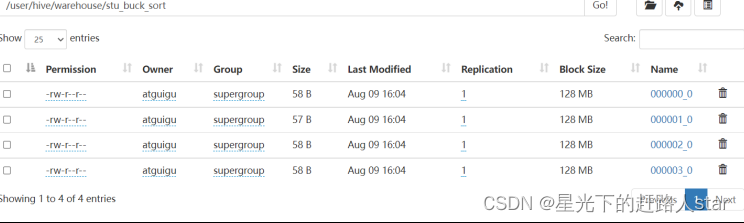
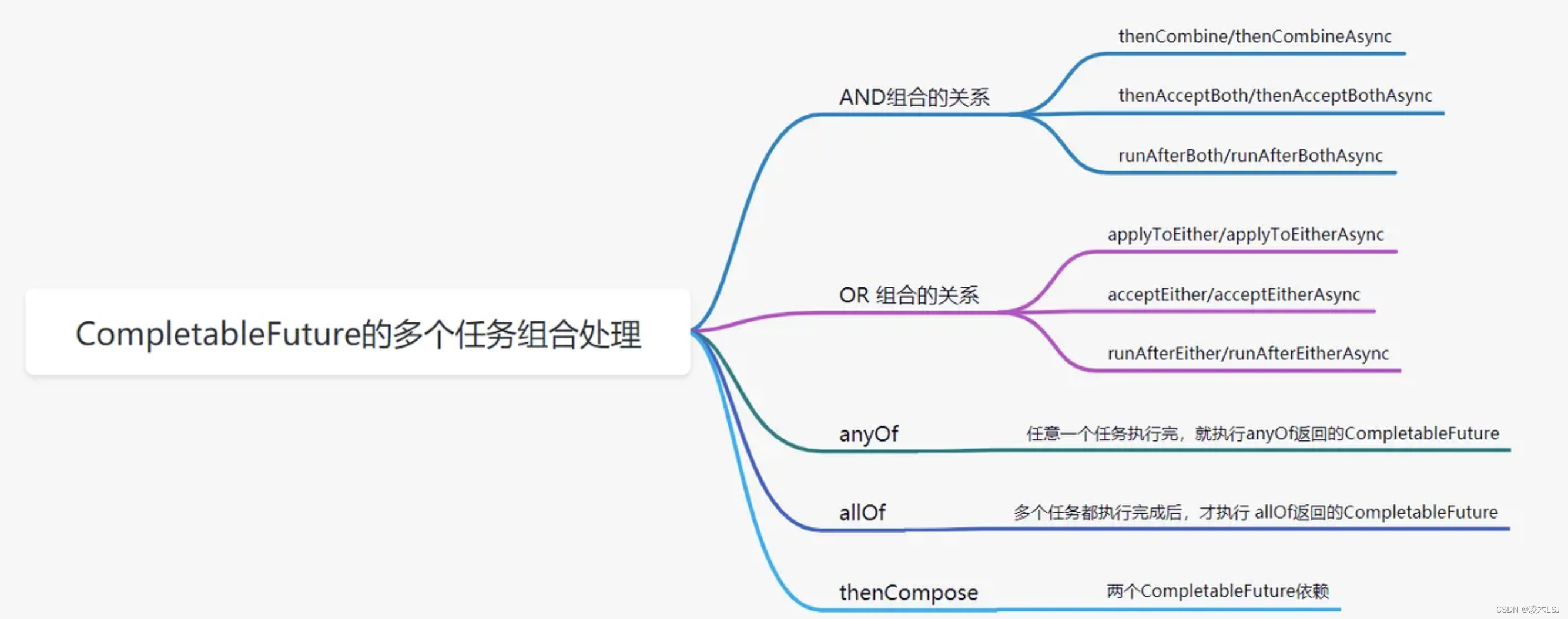
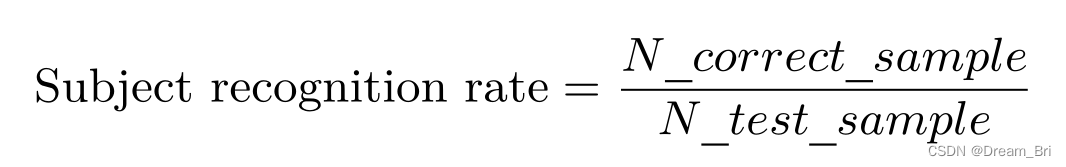如何衡量客户对产品的推荐意愿?净推荐值
趣讲大白话:衡量客户对你好不好
【趣讲信息科技184期】
****************************
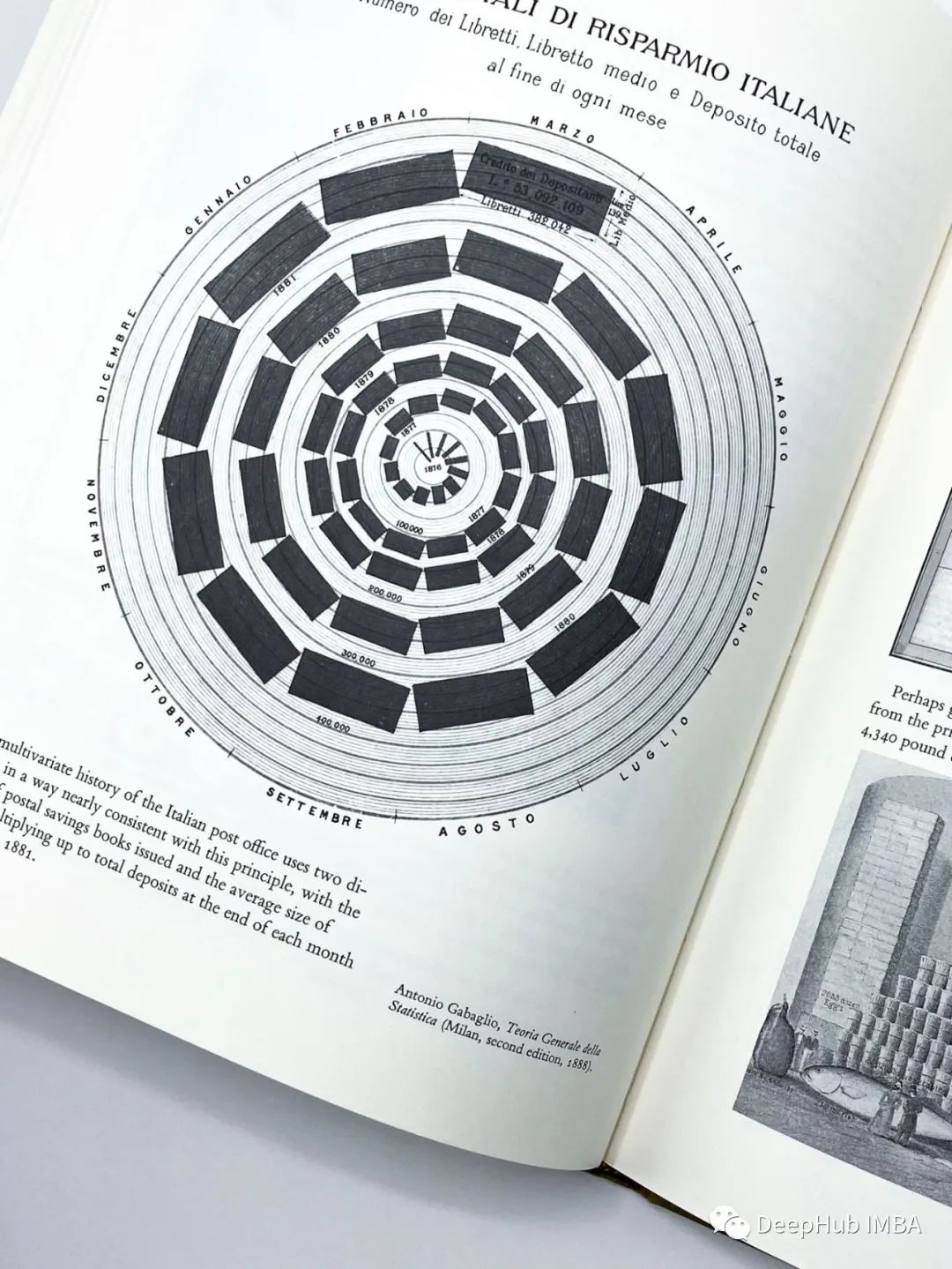
净推荐值(Net Promoter Score,简称NPS)是一种衡量客户忠诚度和推荐意愿的指标。
净推荐值的计算公式为:
NPS = (推荐人数 / 总调查人数) × 100
净推荐值越高,说明客户对公司或品牌的忠诚度和推荐意愿越高。通常认为,净推荐值在70以上是一个好的指标,而在90以上则被认为是非常优秀的指标。
****************************
【#趣讲信息科技#】
#用心琢磨过的学习笔记#
【学习随手笔记】
信息科技为主,企业经营、人生感悟为辅