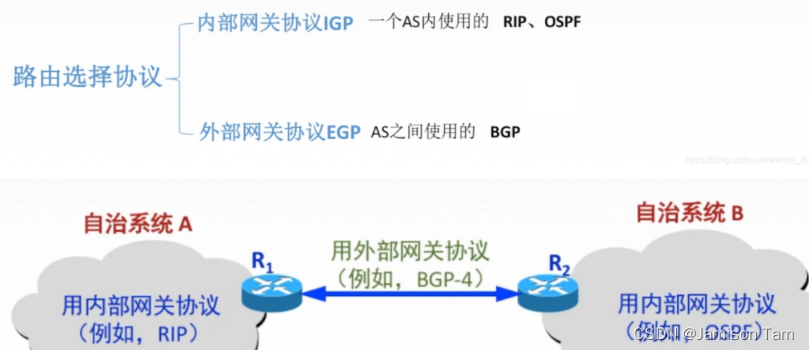
逻辑推理与集合是同一个过程的不同展示方式，这两者具有不同的特点。

逻辑推理通常是一种思维过程、语言文本的形式。

而集合则很容易采用一种可视化的方式进行展示，并且集合很容易进行交集、并集、补集、差集等计算。

把语言的逻辑推理过程转换为集合操作，可以使得推理过程更加简单、更容易理解、更不容易出错。

一个常见的三段论的逻辑推理例子：

人终有一死；
苏格拉底是人；
苏格拉底终有一死。

对应到集合操作可视化为下图

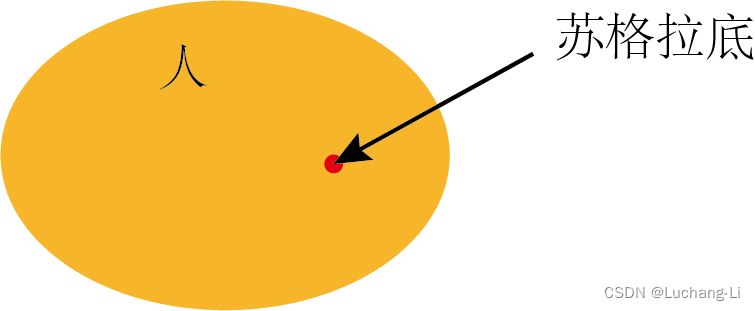
但是怎么根据集合操作得到或者检验最终的结论呢？

这只需要根据：

1. 集合整体成立的条件，其子集成员均成立。

2. 子集满足的特性其父/母集合中其他成员并不一定满足。

上面的例子中，因为苏格拉底是人的子集，因此人的集合整体满足的任何特性，作为人子集的苏格拉底都会满足。但是反过来就不成立：

苏格拉底是人;
苏格拉底终有一死;
人终有一死；

那么具体怎么把自然语言的逻辑推理转换为集合操作呢：

1. 把每个前提条件转换为相应的集合以及集合的交并补差等计算。

2. 得到结论所属的集合。

3. 把结论所属集合作为子集，检验其被包含的更大集合的性质得到该集合的性质。