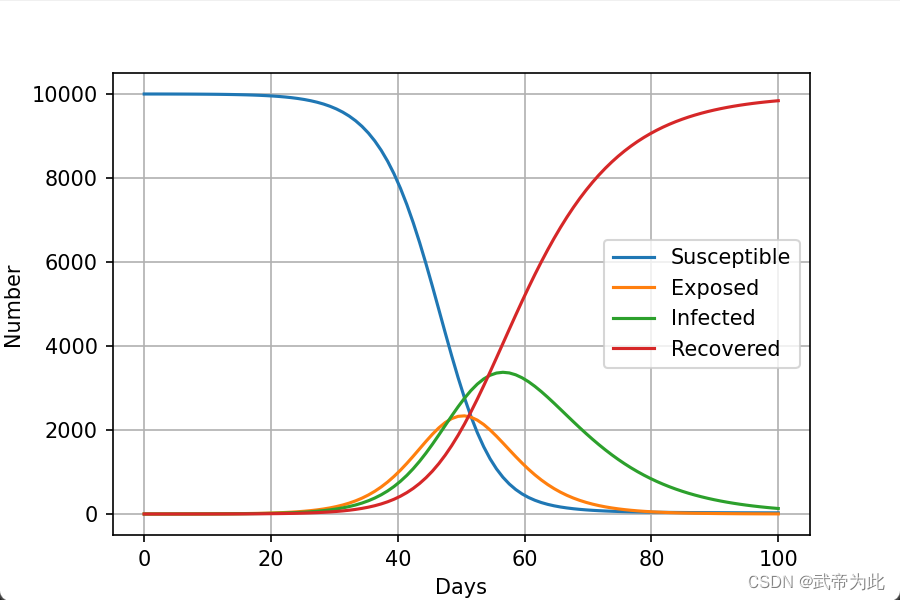
【摘要】 基于物理信息的神经网络(Physics-informed Neural Networks,简称PINNs),是一类用于解决有监督学习任务的神经网络,它不仅能够像传统神经网络一样学习到训练数据样本的分布规律,而且能够学习到数学方程描述的物理定律。与纯数据驱动的神经网络学习相比,PINN在训练过程中施加了物理信息约束,因而能用更少的数据样本学习到更具泛化能力的模型。本文主要解析这种神经网络以及相关应用。
1 论文简介
Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations
https://www.sciencedirect.com/science/article/pii/S0021999118307125
2019年,来自布朗大学应用数学的研究团队提出了一种用物理方程作为运算限制的“物理激发的神经网络” (PINNs) 并发表在了计算物理学领域权威杂志《计算物理学期刊》(Journal of Computational Physics) 上。这篇论文一经发表就获得了大量关注。这篇论文因为代码体系的完整性使得开发人员们很容易上手把相关的学习框架应用到不同领域上去。所以在发表不久之后,一系列不同的PINNs也被其他研究者开发出来。甚至可以不夸张的说,PINN是目前AI物理领域论文中最常见到的框架和词汇之一。
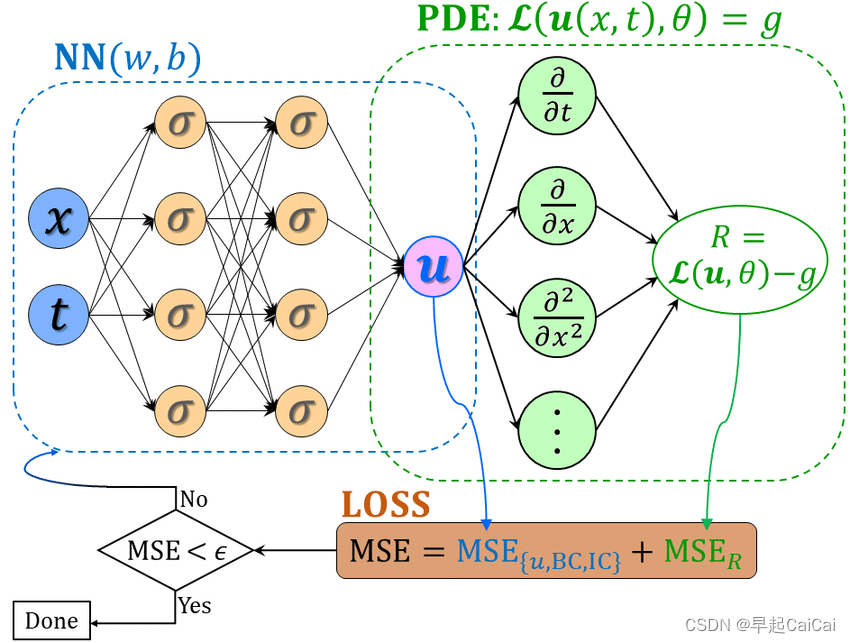
这张图源自?
求解过程
给定一个非线性PDE
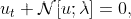
其中
u
u
u 是要求的解,
N
N
N 是非线性偏微分算子,
λ
\lambda
λ 是需要待定的参数。 用一个具体的例子(Burgers方程)来说明主要的想法和步骤:
简单介绍 Burgers方程:
伯格斯方程(Burgers equation) 是一个模拟冲击波的传播和反射的非线性偏微分方程。
Burgers方程是一种常见的非线性对流偏微分方程,它被广泛应用于流体力学、声学、地震学等领域的建模和仿真。Burgers方程可以写成如下形式:
∂ u ∂ t + u ∂ u ∂ x = ν ∂ 2 u ∂ x 2 \frac{\partial u}{\partial t}+u\frac{\partial u}{\partial x}=\nu\frac{\partial^2u}{\partial x^2} ∂t∂u+u∂x∂u=ν∂x2∂2u
其中, u u u是速度场, t t t是时间, x x x是空间位置, ν \nu ν是粘性系数。Burgers方程的左边表示对流项,右边表示扩散项,它们共同描述了速度场的变化规律。
Burgers方程的解析解通常很难求得,因此常常需要使用数值方法进行求解。传统的数值方法包括有限差分法、有限元法等,它们通常需要离散化空间和时间,并且存在精度和稳定性等方面的问题。
参考链接:Burgers方程 - 百度百科
用一个具体的例子(Burgers方程)来说明主要的想法和步骤:
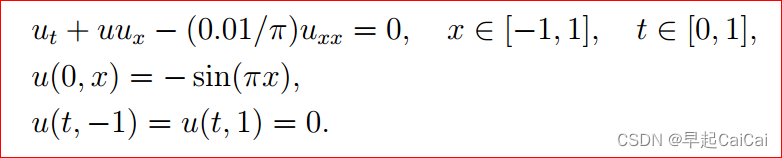
方程1为x空间上的范围为-1到1,时间上的范围为0到1;
约束条件: u u u在 [0,x] 上的方程为 − s i n ( π x ) -sin(\pi x) −sin(πx);这里的0表示t,x表示空间
u u u在 [t,-1] & [t,1]上的方程为0;表示在t时刻,在x为-1或者1时,为0
利用 Neural Networks 来逼近 。 定义损失函数为
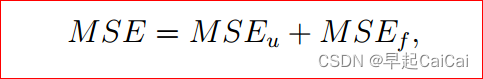
其中:
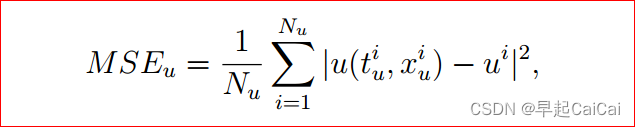
我们来分析一下损失函数。 如果神经网络能很好地求解出PDE的解,那么对于来自初边值的任一个点,其值 M S E u MSE_{u} MSEu 趋于零;对于内部的配置点,因为很好地拟合了微分方程, M S E f MSE_{f} MSEf趋于零,也就是说,损失函数的值为 0 时,我们便可以说在训练集上每个点都有神经网络的值趋于真实值 。这样便将问题转化为如何优化损失函数。利用
神经网络的反向传播机制和L-BFGS便可以求解。
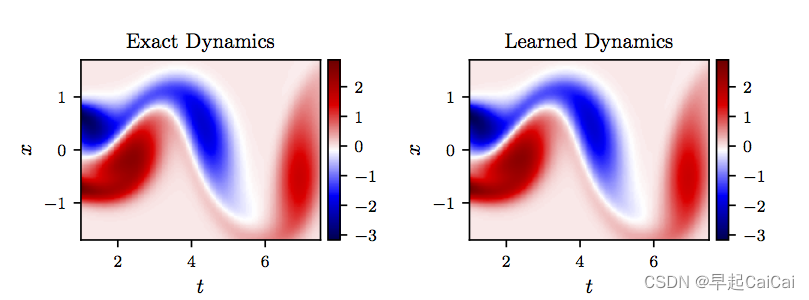
利用神经网络的反向传播机制和L-BFGS便可以求解。 作者使用了
tensorflow1.13版本来求解。
参考链接:基本模型 PINNs : Physics Informed Neural Networks
相关应用论文
Physics-Informed Neural Network Super Resolution for Advection-Diffusion Models
物理信息神经网络超分辨率方法用于平流扩散模型
https://arxiv.org/abs/2011.02519
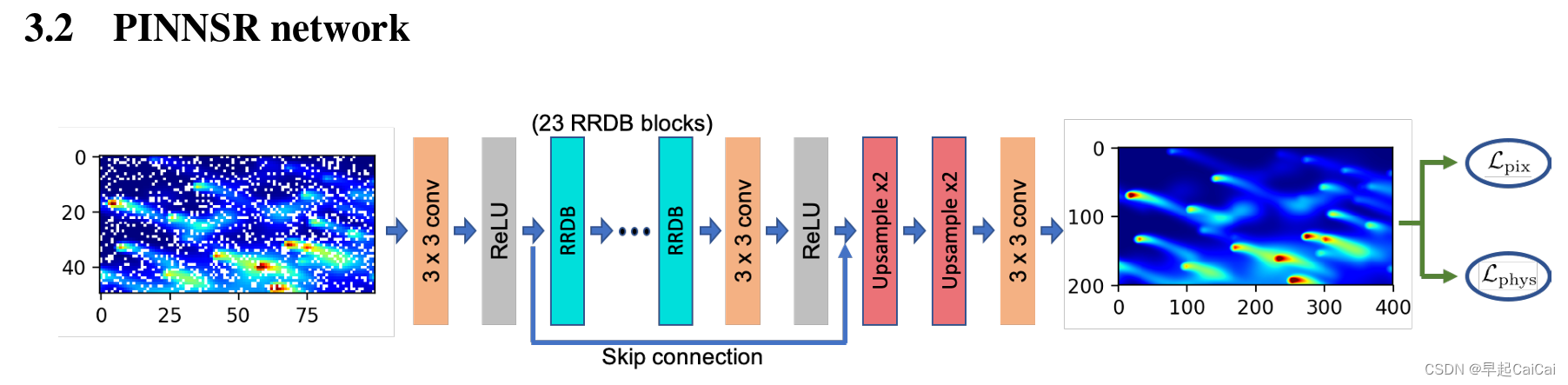
图1:PINNSR的网络结构。输入的低分辨率图像LR是通过在粗网格上进行模拟生成的,而不是从高分辨率图像HR进行下采样。随机像素(白色)被删除以模拟缺失像素。总损失是像素损失 L p i x L_{pix} Lpix 和物理一致性损失 L p h y s L_{phys} Lphys 的加权和。
电力系统动力学求解
Physics-Informed Neural Networks for Power Systems
PINNs for Power Systems
https://ieeexplore.ieee.org/abstract/document/9282004
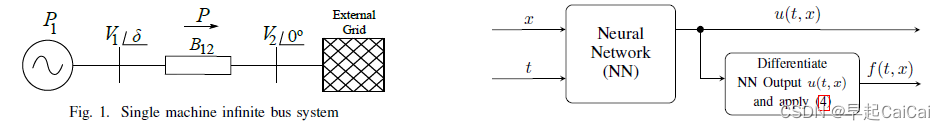
金属表面声波裂缝检测
PHYSICS-INFORMED NEURAL NETWORK FOR ULTRASOUND NONDESTRUCTIVE QUANTIFICATION OF SURFACE BREAKING CRACKS
PINNs for 超声无损评估表面裂纹的数量化
https://link.springer.com/article/10.1007/s10921-020-00705-1

Reference
物理神经网络(PINN)解读
https://blog.csdn.net/waitingwinter/article/details/103979339

![[转载]Nginx 使用 X-Accel-Redirect 实现静态文件下载的统计、鉴权、防盗链、限速等](https://img-blog.csdnimg.cn/img_convert/ea28657bf08077d6373ea049f78454fa.png)