预计阅读时间:10分钟
一、简介
霍夫曼树常处理符号编写工作。根据整组数据中符号出现的频率高低,决定如何给符号编码。如果符号出现的频率越高,则给符号的码越短,相反符号的号码越长。
相关术语
路径:从书中一个节点到另一个节点之间的分支构成这两个节点的路径。
路径长度:即路径上有多少个分支。
树的路径长度:从树根到每一个节点的路径长度之和。
带权路径长度:从根节点到叶子节点的路程长度与该节点权值的积。
树的带权路径长度:树中所有带权叶子节点的路径长度之和。
霍夫曼编码就是再霍夫曼树上进行实现的。
从树根开始,从待译电文中逐个取码。若编码为0,就往左走;编码为1,就往右走,一旦到达了叶子节点,就是译出了一个字符;在从根出发,直到电文结束。
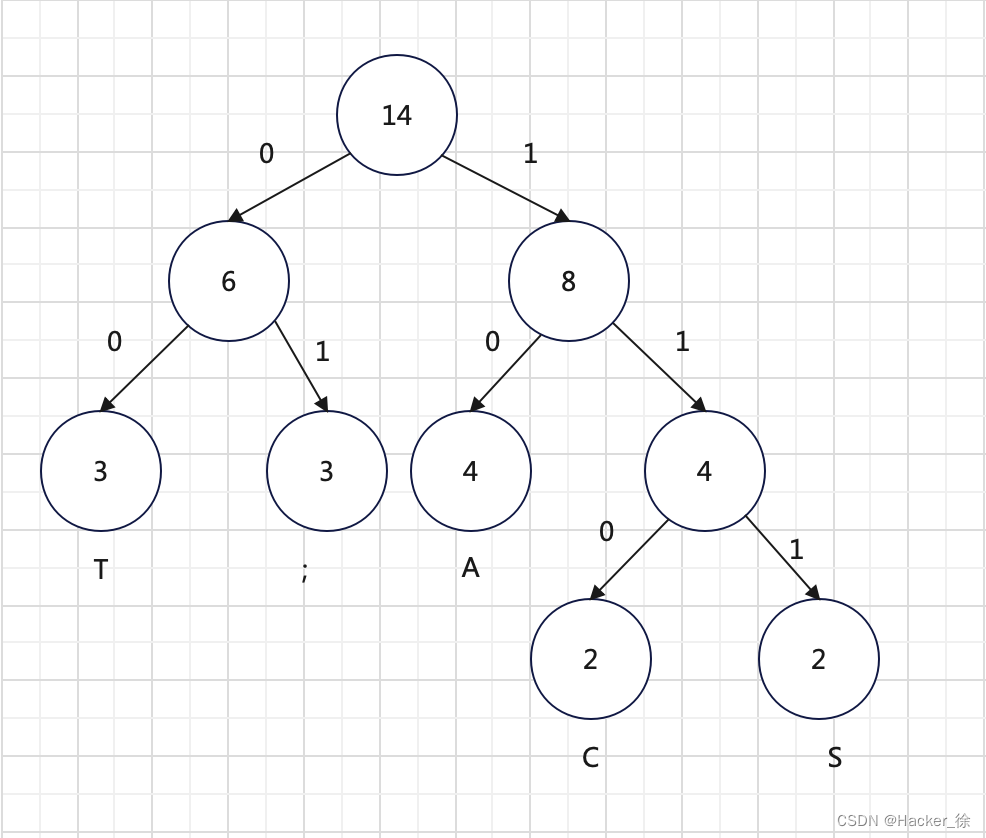
T:00 ;:00 A:10 C:110 S:111
参考图1:
电文是{CAS;CAT;SAT;AT}
编码就是11010111011101000011111000011000
电文如果是1101000
译文就是CAT
假设我们要给一个英文单字"FORGET"进行霍夫曼编码。
演算过程
(一)进行编码前,要先创建一个霍夫曼树。
⒈将每个英文字母依照出现频率由小排到大,最小在左,如Fig.1;
⒉每个字母都代表一个终端节点(叶节点),比较F.O.R.G.E.T六个字母中每个字母的出现频率,将最小的两个字母频率相加合成一个新的节点。如Fig.2所示,发现F与O的频率最小,故相加2+3=5;
⒊比较5.R.G.E.T,发现R与G的频率最小,故相加4+4=8;
⒋比较5.8.E.T,发现5与E的频率最小,故相加5+5=10;
⒌比较8.10.T,发现8与T的频率最小,故相加8+7=15;
⒍最后剩10.15,没有可以比较的对象,相加10+15=25。
最后产生的树状图就是霍夫曼树。
(二)进行编码
1.给霍夫曼树的所有左链接'0'与右链接'1';
2.从树根至树叶依序记录所有字母的编码。
二、代码实现
#include <bits/stdc++.h>
using namespace std;
//霍夫曼树的结构
typedef struct
{
//叶子结点权值
unsigned int weight;
//指向双亲,和孩子结点的指针
unsigned int parent;
unsigned int lChild;
unsigned int rChild;
}Node,*HuffmanTree;
//动态分配数组,存储哈夫曼编码
typedef char *HuffmanCode;
//选择两个parent为0,且weight最小的结点s1和s2的方法实现
//n 为叶子结点的总数,s1和 s2两个指针参数指向要选取出来的两个权值最小的结点
void select(HuffmanTree *huffmanTree,int n,int *s1,int *s2)
{
//标记i
int i=0;
//记录最小权值
int min;
//遍历全部结点,找出单节点
for(i=1; i<=n; i++)
{
//如果此结点的父亲没有,那么把结点号赋值给 min,跳出循环
if((*huffmanTree)[i].parent==0)
{
min=i;
break;
}
}
//继续遍历全部结点,找出权值最小的单节点
for(i=1; i<=n; i++)
{
//如果此结点的父亲为空,则进入 if
if((*huffmanTree)[i].parent==0)
{
//如果此结点的权值比 min 结点的权值小,那么更新 min 结点,否则就是最开始的 min
if((*huffmanTree)[i].weight<(*huffmanTree)[min].weight)
{
min=i;
}
}
}
//找到了最小权值的结点,s1指向
*s1=min;
//遍历全部结点
for(i=1; i<=n; i++)
{
//找出下一个单节点,且没有被 s1指向,那么i 赋值给 min,跳出循环
if((*huffmanTree)[i].parent==0&&i!=(*s1))
{
min=i;
break;
}
}
//继续遍历全部结点,找到权值最小的那一个
for(i=1; i<=n; i++)
{
if((*huffmanTree)[i].parent==0&&i!=(*s1))
{
//如果此结点的权值比 min 结点的权值小,那么更新 min 结点,否则就是最开始的 min
if((*huffmanTree)[i].weight<(*huffmanTree)[min].weight)
{
min=i;
}
}
}
//s2指针指向第二个权值最小的叶子结点
*s2=min;
}
//创建霍夫曼树并求霍夫曼编码的算法如下,w数组存放已知的n个权值
void createHuffmanTree(HuffmanTree *huffmanTree, int w[], int n)
{
//m为哈夫曼树总共的结点数,n为叶子结点数
int m=2*n-1;
//s1和s2为两个当前结点里,要选取的最小权值的结点
int s1;
int s2;
//标记
int i;
//创建哈夫曼树的结点所需的空间,m+1,代表其中包含一个头结点
*huffmanTree=(HuffmanTree)malloc((m+1)*sizeof(Node));
//1--n号存放叶子结点,初始化叶子结点,结构数组来初始化每个叶子结点,初始的时候看做一个个单个结点的二叉树
for(i=1; i<=n; i++)
{
//其中叶子结点的权值是 w[n]数组来保存
(*huffmanTree)[i].weight=w[i];
//初始化叶子结点(单个结点二叉树)的孩子和双亲,单个结点,也就是没有孩子和双亲,==0
(*huffmanTree)[i].lChild=0;
(*huffmanTree)[i].parent=0;
(*huffmanTree)[i].rChild=0;
}
//非叶子结点的初始化
for(i=n+1; i<=m; i++)
{
(*huffmanTree)[i].weight=0;
(*huffmanTree)[i].lChild=0;
(*huffmanTree)[i].parent=0;
(*huffmanTree)[i].rChild=0;
}
printf("\n HuffmanTree: \n");
//创建非叶子结点,建哈夫曼树
for(i=n+1; i<=m; i++)
{
//在(*huffmanTree)[1]~(*huffmanTree)[i-1]的范围内选择两个parent为0
//且weight最小的结点,其序号分别赋值给s1、s2
select(huffmanTree,i-1,&s1,&s2);
//选出的两个权值最小的叶子结点,组成一个新的二叉树,根为 i 结点
(*huffmanTree)[s1].parent=i;
(*huffmanTree)[s2].parent=i;
(*huffmanTree)[i].lChild=s1;
(*huffmanTree)[i].rChild=s2;
//新的结点i的权值
(*huffmanTree)[i].weight=(*huffmanTree)[s1].weight + (*huffmanTree)[s2].weight;
printf("%d (%d, %d)\n",(*huffmanTree)[i].weight,(*huffmanTree)[s1].weight,(*huffmanTree)[s2].weight);
}
printf("\n");
}
//哈夫曼树建立完毕,从 n 个叶子结点到根,逆向求每个叶子结点对应的哈夫曼编码
void creatHuffmanCode(HuffmanTree *huffmanTree, HuffmanCode *huffmanCode, int n)
{
//指示biaoji
int i;
//编码的起始指针
int start;
//指向当前结点的父节点
int p;
//遍历 n 个叶子结点的指示标记 c
unsigned int c;
//分配n个编码的头指针
huffmanCode=(HuffmanCode *)malloc((n+1) * sizeof(char *));
//分配求当前编码的工作空间
char *cd = (char *)malloc(n * sizeof(char));
//从右向左逐位存放编码,首先存放编码结束符
cd[n-1] = '\0';
//求n个叶子结点对应的哈夫曼编码
for(i = 1; i <= n; i++)
{
//初始化编码起始指针
start = n - 1;
//从叶子到根结点求编码
for(c = i, p = (*huffmanTree)[i].parent; p != 0; c = p, p = (*huffmanTree)[p].parent)
{
if( (*huffmanTree)[p].lChild == c)
{
//从右到左的顺序编码入数组内
cd[--start] = '0'; //左分支标0
}
else
{
cd[--start] = '1'; //右分支标1
}
}// end of for
//为第i个编码分配空间
huffmanCode[i] = (char *)malloc((n - start) * sizeof(char));
strcpy(huffmanCode[i], &cd[start]);
}
free(cd);
//打印编码序列
for(i=1; i<=n; i++)
{
printf("HuffmanCode of %3d is %s\n", (*huffmanTree)[i].weight, huffmanCode[i]);
}
printf("\n");
}
int main()
{
HuffmanTree HT;
HuffmanCode HC;
int *w,i,n,wei,m;
printf("\nn = " );
scanf("%d",&n);
w=(int *)malloc((n+1)*sizeof(int));
printf("\ninput the %d element's weight:\n",n);
for(i=1; i<=n; i++)
{
printf("%d: ",i);
fflush(stdin);
scanf("%d",&wei);
w[i]=wei;
}
createHuffmanTree(&HT, w, n);
creatHuffmanCode(&HT,&HC,n);
return 0;
}参考文献:
【C++】霍夫曼树与编码(原理详细&代码注释)_米莱虾的博客-CSDN博客哈夫曼树(最优二叉树)❥分享大一所做笔记❥知识点解析WPL:树的所有叶结点的带权路径长度之和,称为树的带权路径长度表示为WPL不带权值的话,完全(满)二叉树的路径长度最小最优二叉树 != 最佳判定树权值相等或不存在的话,最优二叉树就是完全二叉树代码(注释详细)#include <bits/stdc++.h>using namespace std;//haffman 树的结构ty...https://blog.csdn.net/Luoxiaobaia/article/details/122460555以上就是本文的全部内容啦!感谢阅读!