剑指 Offer 03. 数组中重复的数字

在一个长度为 n 的数组 nums 里的所有数字都在 0～n-1 的范围内。数组中某些数字是重复的，但不知道有几个数字重复了，也不知道每个数字重复了几次。请找出数组中任意一个重复的数字。

示例 1：

输入：
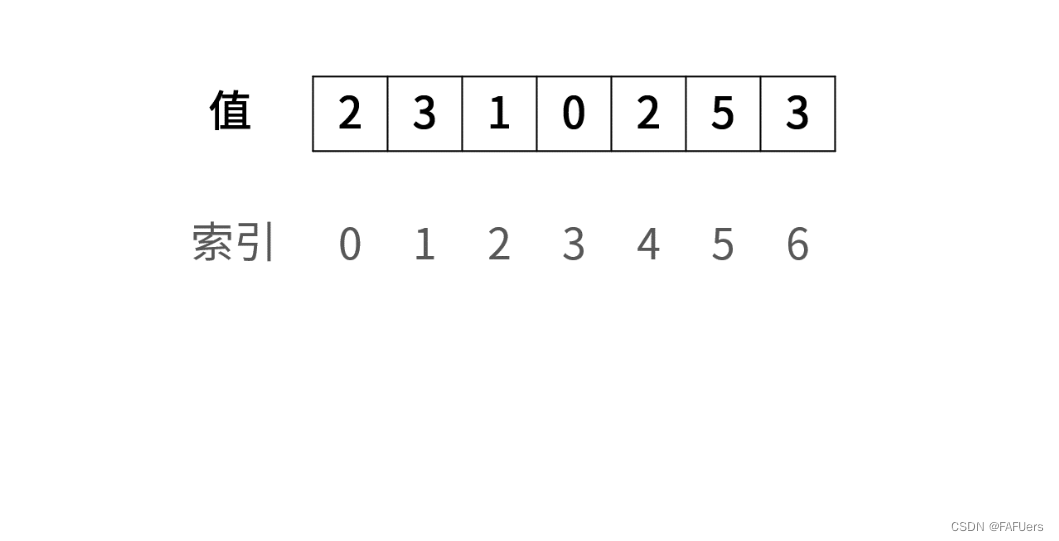
[2, 3, 1, 0, 2, 5, 3]
输出：2 或 3 

class Solution {
    public int findRepeatNumber(int[] nums) {

    }
}

解题思路

数组元素的 索引 和 值 是 一对多 的关系。
因此，可遍历数组并通过交换操作，使元素的 索引 与 值 一一对应（即 nums[i] = i ）。因而，就能通过索引映射对应的值，起到与字典等价的作用。

遍历中，第一次遇到数字 x 时，将其交换至索引 x 处；而当第二次遇到数字 x 时，一定有 nums[x]=x ，此时即可得到一组重复数字。

算法流程：
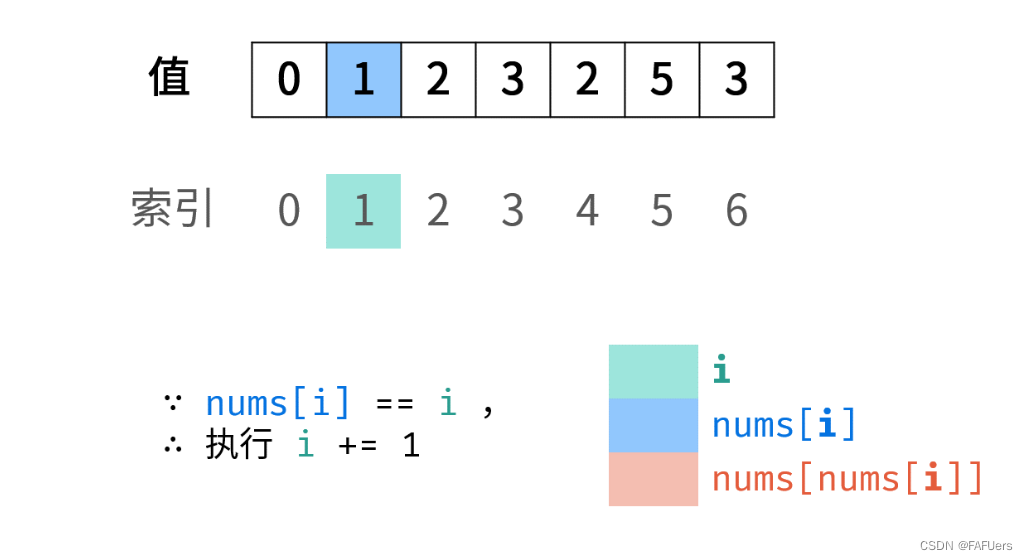
遍历数组 nums ，设索引初始值为 i = 0 :

若 nums[i] =i ： 说明此数字已在对应索引位置，无需交换，因此跳过；
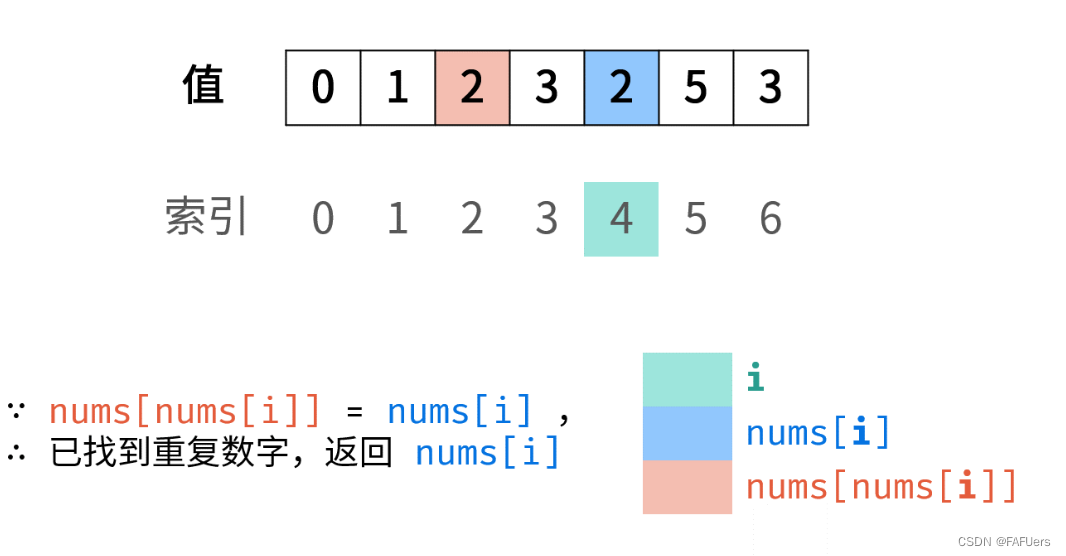
若 nums[nums[i]] = nums[i] ： 代表索引 nums[i]处和索引 i 处的元素值都为nums[i] ，即找到一组重复值，返回此值 nums[i] ；
否则： 交换索引为 i 和 nums[i] 的元素值，将此数字交换至对应索引位置。
若遍历完毕尚未返回，则返回 -1 。

 

 

 

 

 

 

 

 代码如下：

class Solution {
    public int findRepeatNumber(int[] nums) {
        int i = 0;
        while(i < nums.length) {
            if(nums[i] == i) {
                i++;
                continue;
            }
            if(nums[nums[i]] == nums[i]) return nums[i];
            int tmp = nums[i];
            nums[i] = nums[tmp];
            nums[tmp] = tmp;
        }
        return -1;
    }
}

---

剑指 Offer 53. 在排序数组中查找数字

统计一个数字在排序数组中出现的次数。

示例 1:

输入: nums = [5,7,7,8,8,10], target = 8
输出: 2
示例 2:

输入: nums = [5,7,7,8,8,10], target = 6
输出: 0

class Solution {
    public int search(int[] nums, int target) {

    }
}

解题思路

算法解析：
初始化： 左边界 i = 0 ，右边界 j = len(nums) - 1 。
循环二分： 当闭区间 [i, j]无元素时跳出；
计算中点 m = (i + j) / 2（向下取整）；
若 nums[m] < target ，则target 在闭区间[m+1,j] 中，因此执行 i = m + 1；
若 nums[m] > target ，则 target 在闭区间 [i, m - 1] 中，因此执行 j = m - 1；
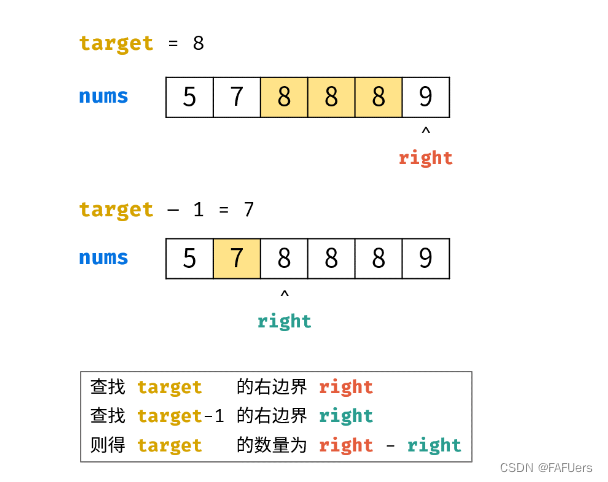
若 nums[m] = target，则右边界right 在闭区间[m+1,j] 中；左边界left 在闭区间 [i,m−1] 中。因此分为以下两种情况：
若查找 右边界 right ，则执行 i = m + 1；（跳出时 i 指向右边界）
若查找 左边界 left ，则执行j=m−1 ；（跳出时 j 指向左边界）
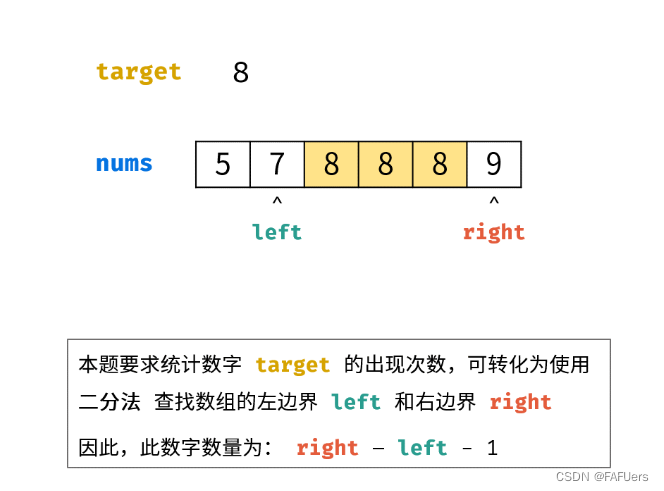
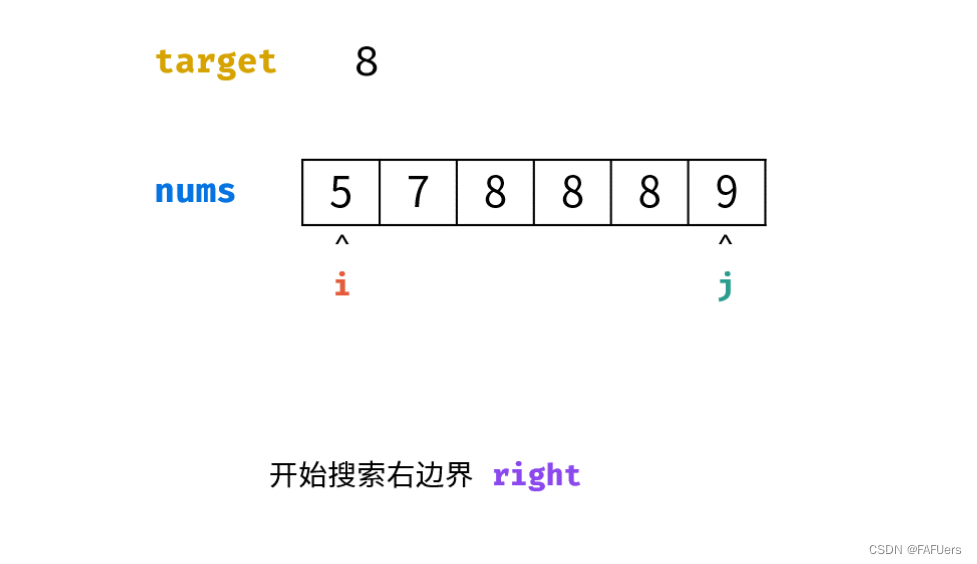
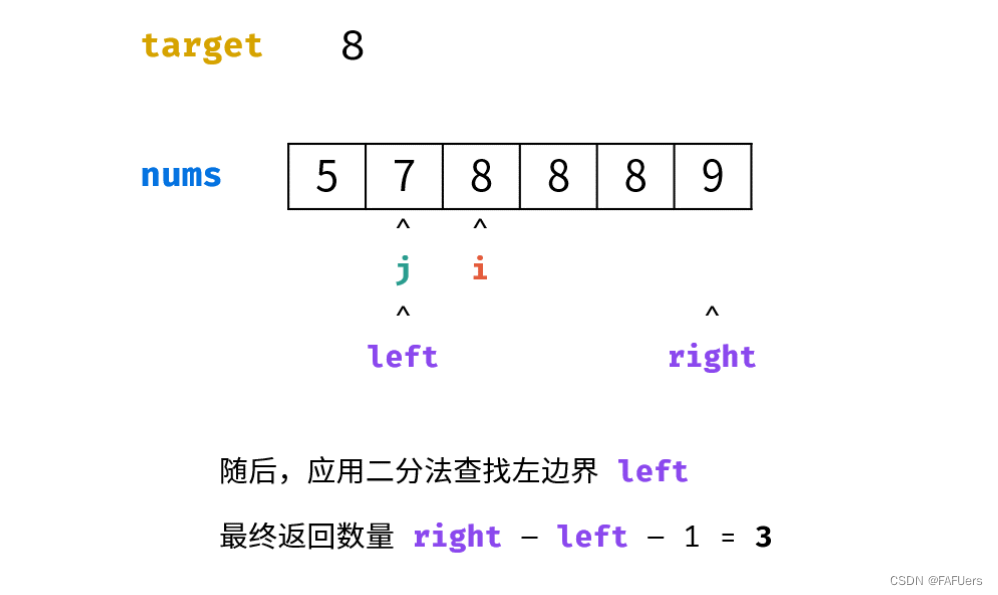
返回值： 应用两次二分，分别查找right 和 left ，最终返回 right - left - 1即可

 

 

 

 

 

代码如下：

class Solution {
    public int search(int[] nums, int target) {
        // 搜索右边界 right
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= target) i = m + 1;
            else j = m - 1;
        }
        int right = i;
        // 若数组中无 target ，则提前返回
        if(j >= 0 && nums[j] != target) return 0;
        // 搜索左边界 right
        i = 0; j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] < target) i = m + 1;
            else j = m - 1;
        }
        int left = j;
        return right - left - 1;
    }
}

以上代码显得比较臃肿（两轮二分查找代码冗余）。为简化代码，可将二分查找右边界 right 的代码 封装至函数 helper() 。 

 

class Solution {
    public int search(int[] nums, int target) {
        return helper(nums, target) - helper(nums, target - 1);
    }
    int helper(int[] nums, int tar) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] <= tar) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}

---

剑指 Offer 53. 0～n-1 中缺失的数字 

一个长度为n-1的递增排序数组中的所有数字都是唯一的，并且每个数字都在范围0～n-1之内。在范围0～n-1内的n个数字中有且只有一个数字不在该数组中，请找出这个数字。

示例 1:

输入: [0,1,3]
输出: 2
示例 2:

输入: [0,1,2,3,4,5,6,7,9]
输出: 8

class Solution {
    public int missingNumber(int[] nums) {

    }
}

解题思路

算法解析：
初始化： 左边界 i = 0，右边界j=len(nums)−1 ；代表闭区间[i,j] 。
循环二分： 当 i≤j 时循环 （即当闭区间 [i,j] 为空时跳出） ；
计算中点 m=(i+j)/2 ；
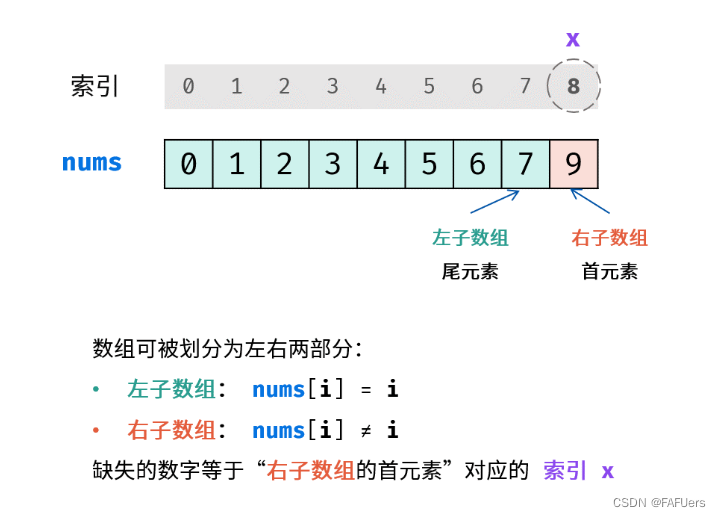
若 nums[m] = m ，则 “右子数组的首位元素” 一定在闭区间[m+1,j] 中，因此执行i=m+1；
若 nums[m] !=m ，则 “左子数组的末位元素” 一定在闭区间 [i,m−1] 中，因此执行j=m−1；
返回值： 跳出时，变量 i 和 j 分别指向 “右子数组的首位元素” 和 “左子数组的末位元素” 。因此返回 i 即可。

 

 

 

 

 

代码如下：

class Solution {
    public int missingNumber(int[] nums) {
        int i = 0, j = nums.length - 1;
        while(i <= j) {
            int m = (i + j) / 2;
            if(nums[m] == m) i = m + 1;
            else j = m - 1;
        }
        return i;
    }
}