图像变换
下面的所有变换假设都是针对一幅图像,即一个三维数组(HWC),这里为简单起见,假设图像都是单通道(C=1)的。
- ( x , y ) (x,y) (x,y): 原图像中某一点 A 的位置
- ( x ′ , y ′ ) (x′,y′) (x′,y′): 变换后图像中 A 点对应的位置
几种常用的线性变换
平移(translation)
若将原图像沿 x和 y方向分别平移δx和δy,即:
x
′
=
x
+
δ
x
y
′
=
x
+
δ
y
x′=x+δx\\y′=x+δy
x′=x+δxy′=x+δy
写成矩阵形式如下:
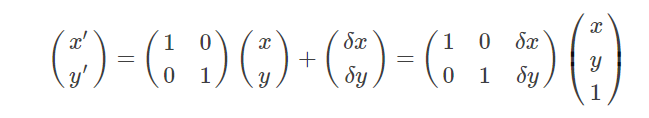
缩放(Scaling)
假设将图像分别沿 x和 y方向分别缩放 p倍和 q倍,且 p>0,q>0,即:
x ′ = p x y ′ = q y x′=px\\y′=qy x′=pxy′=qy
写成矩阵形式如下:
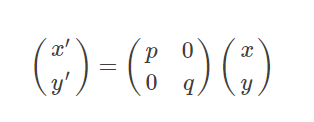
旋转(Rotation)
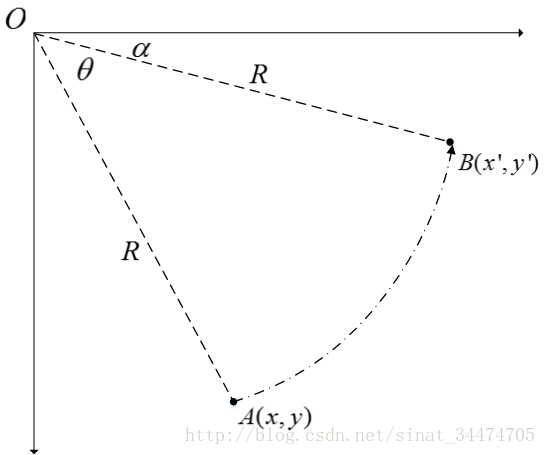
如上图所示,点 A旋转θ角到点 B,由 B点可得
x ′ = R c o s α y ′ = R s i n α x′=Rcosα\\y′=Rsinα x′=Rcosαy′=Rsinα
由A点可得:
x = R c o s ( α + θ ) = R c o s ( α ) c o s θ + R s i n ( α ) s i n ( θ ) y = R s i n ( α + θ ) = R s i n ( α ) c o s θ − R c o s ( α ) s i n ( θ ) x=Rcos(α+θ)=Rcos(α)cosθ+Rsin(α)sin(θ)\\ y=Rsin(α+θ)=Rsin(α)cosθ−Rcos(α)sin(θ) x=Rcos(α+θ)=Rcos(α)cosθ+Rsin(α)sin(θ)y=Rsin(α+θ)=Rsin(α)cosθ−Rcos(α)sin(θ)
整理可得:
x
′
=
x
c
o
s
θ
+
y
s
i
n
θ
y
′
=
−
x
s
i
n
θ
+
y
c
o
s
θ
x′=xcosθ+ysinθ\\ y′=−xsinθ+ycosθ
x′=xcosθ+ysinθy′=−xsinθ+ycosθ
写成矩阵形式如下:
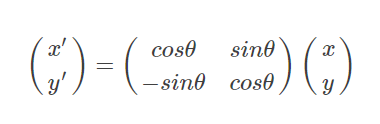
剪切 (Shear)
剪切变换相当于将图片沿 x和 y两个方向拉伸,且 x方向拉伸长度与 y有关,y方向拉伸长度与 x有关,用矩阵形式表示前切变换如下:
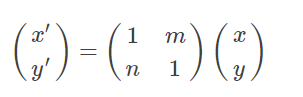
仿射变换
其实上面几种常见变换都可以用同一种变换来表示,就是仿射变换,它有更一般的形式,如下:
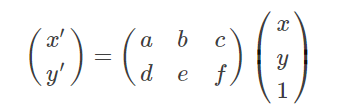
-
当 a = e = 1 , b = c = d = f = 0 a=e=1,b=c=d=f=0 a=e=1,b=c=d=f=0为恒等变换,即输入图像不变;
-
当 a = e = 1 , b = d = 0 a=e=1,b=d=0 a=e=1,b=d=0时,为平移变换;
-
当 a = c o s θ , b = s i n θ , d = − s i n θ , e = c o s θ , c = f = 0 a=cosθ,b=sinθ,d=−sinθ,e=cosθ,c=f=0 a=cosθ,b=sinθ,d=−sinθ,e=cosθ,c=f=0时,为旋转变换;
-
当 a = e = 1 , c = f = 0 a=e=1,c=f=0 a=e=1,c=f=0时,为剪切变换。
-
当 6 个参数取其他值时,为一般的仿射变换,效果相当于从不同的位置看同一个目标。
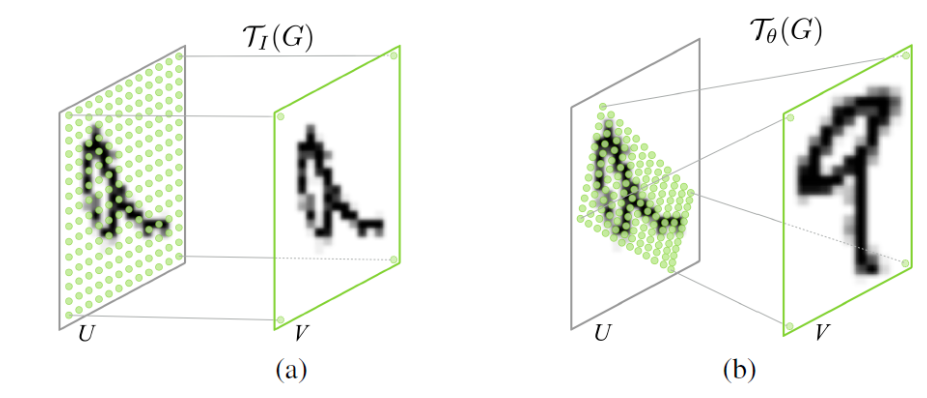
双线性插值
在对图像进行仿射变换时,会出现一个问题,当原图像中某一点的坐标映射到变换后图像时,坐标可能会出现小数(如图 2 所示),而我们知道,图像上某一像素点的位置坐标只能是整数,那该怎么办?这时候双线性插值就起作用了。
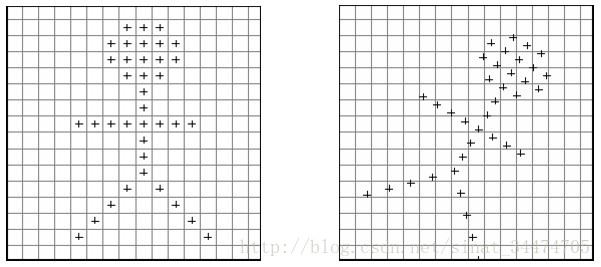
在实现时我们通常将变换后图像上所有的位置映射到原图像计算(这样做比正向计算方便得多),即依次遍历变换后图像上所有的像素点,根据仿射变换矩阵计算出映射到原图像上的坐标(可能出现小数),然后用双线性插值,根据该点周围 4 个位置的值加权平均得到该点值。过程可用如下公式表示:
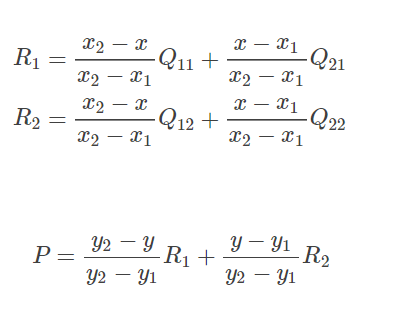
将 (11) 代入 (12) 整理得:
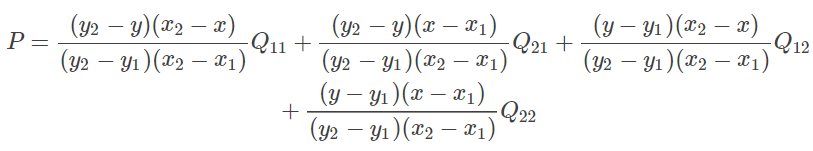
因为Q11,Q12,Q21,Q22
是相邻的四个点,所以 y 2 − y 1 = 1 , x 2 − x 1 = 1 y2−y1=1,x2−x1=1 y2−y1=1,x2−x1=1,则(13)可化简为:
P = ( y 2 − y ) ( x 2 − x ) Q 11 + ( y 2 − y ) ( x − x 1 ) Q 21 + ( y − y 1 ) ( x 2 − x ) Q 12 + ( y − y 1 ) ( x − x 1 ) Q 22 P=(y_2-y)(x_2-x)Q_{11}+(y_2-y)(x-x_1)Q_{21}+(y-y_1)(x_2-x)Q_{12}+(y-y_1)(x-x_1) Q_{22} P=(y2−y)(x2−x)Q11+(y2−y)(x−x1)Q21+(y−y1)(x2−x)Q12+(y−y1)(x−x1)Q22
class Net(nn.Module):
def __init__(self):
super(Net, self).__init__()
self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
self.conv2_drop = nn.Dropout2d()
self.fc1 = nn.Linear(320, 50)
self.fc2 = nn.Linear(50, 10)
# 空间变换网络 Spatial transformer localization-network
self.localization = nn.Sequential(
nn.Conv2d(1, 8, kernel_size=7),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True),
nn.Conv2d(8, 10, kernel_size=5),
nn.MaxPool2d(2, stride=2),
nn.ReLU(True)
)
# 3*2的仿射变换矩阵的回归量 Regressor for the 3 * 2 affine matrix
self.fc_loc = nn.Sequential(
nn.Linear(10 * 3 * 3, 32),
nn.ReLU(True),
nn.Linear(32, 3 * 2)
)
# 用恒等变换初始化仿射变换矩阵的权重和偏置 Initialize the weights/bias with identity transformation
self.fc_loc[2].weight.data.zero_()
self.fc_loc[2].bias.data.copy_(torch.tensor([1, 0, 0, 0, 1, 0], dtype=torch.float))
# Spatial transformer network forward function
def stn(self, x):
xs = self.localization(x)
xs = xs.view(-1, 10 * 3 * 3)
theta = self.fc_loc(xs)
theta = theta.view(-1, 2, 3)
grid = F.affine_grid(theta, x.size())
x = F.grid_sample(x, grid)
return x
def forward(self, x):
# transform the input
x = self.stn(x)
# Perform the usual forward pass
x = F.relu(F.max_pool2d(self.conv1(x), 2))
x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
x = x.view(-1, 320)
x = F.relu(self.fc1(x))
x = F.dropout(x, training=self.training)
x = self.fc2(x)
return F.log_softmax(x, dim=1)









![[附源码]计算机毕业设计校园招聘系统Springboot程序](https://img-blog.csdnimg.cn/7870e91e47d445bf840de01854ffb689.png)