欢迎观看我的博客，如有问题交流，欢迎评论区留言，一定尽快回复！（大家可以去看我的专栏，是所有文章的目录）
文章字体风格：
红色文字表示：重难点
蓝色文字表示：思路以及想法
　
如果大家觉得有帮助的话，感谢大家帮忙点赞！收藏！转发！

本博客要从头看到尾，才能清楚本篇的逻辑。

1. 什么是负环

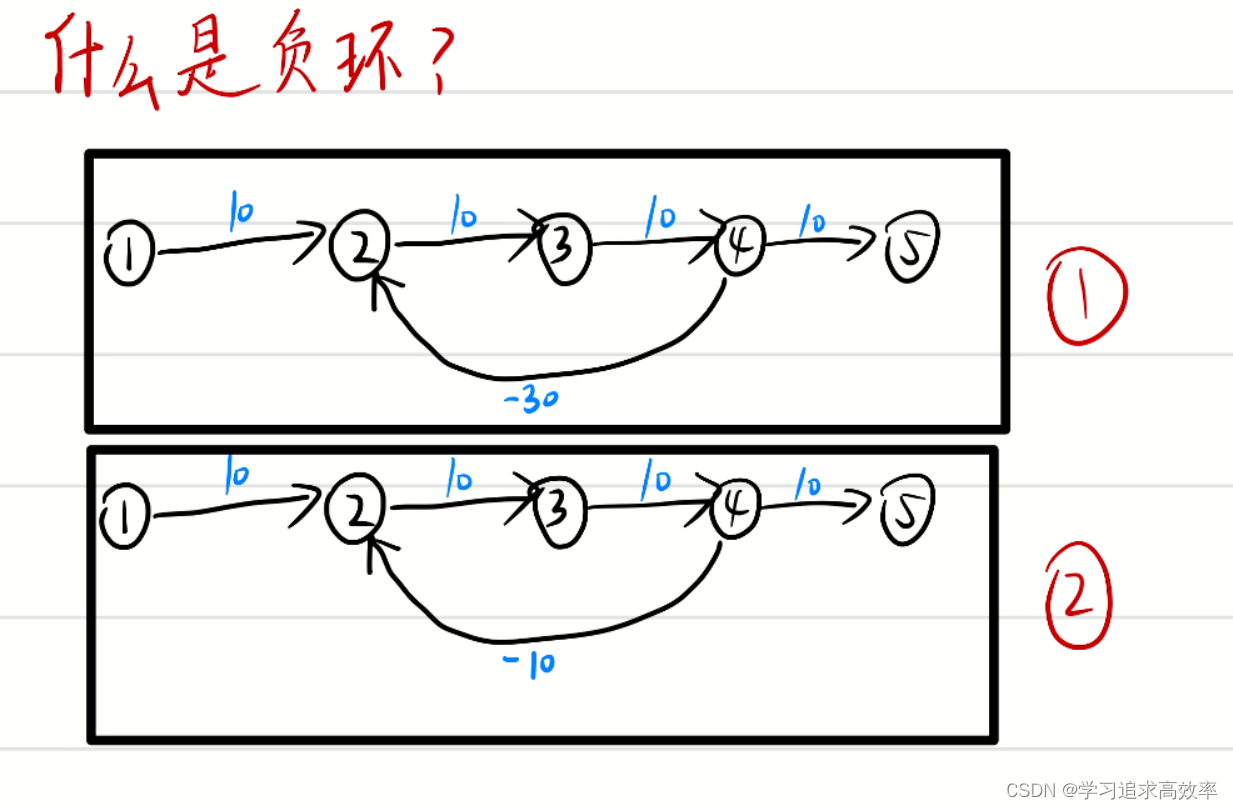
图1中：2 到 3 到 4 到 2 路径长度为 -10
图2中：2 到 3 到 4 到 2 路径长度为 10

图1才叫负环
图2不是负环

2. 出现负环会怎么样

但出现负环的时候，如果我们要去求1到n的最短路，那么过程中，一定会在这个负环中一直转圈，导致路程可以变为负无穷

3. 怎么判断图中是否有负环？

综上，我们就采取求最小路径的方式（但是本题不是求最短路），当我们求最短路径的过程中，发现有一段路径重复走，那么就说明一定出现了负环

问题来了：怎么判断某段路径在重复走

我们想，1到n号点 最多才可能走了n-1条边

如果我们发现 到某点时 已经走了 大于等于n条边，那么一定就是有负环了

由于我们不知道 1 到 x点最多可能有多少条边，但一定不会超过 n - 1 条边，所以我们就都用 大于等于n条边去判断

例题 spfa判断负环

原题链接

#include <cstring>
#include <iostream>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 2010, M = 10010;

int n, m;
int h[N], w[M], e[M], ne[M], idx;
int dist[N], cnt[N];
bool st[N];

void add(int a, int b, int c)
{
    e[idx] = b, w[idx] = c, ne[idx] = h[a], h[a] = idx ++ ;
}

bool spfa()
{
    queue<int> q;

    for (int i = 1; i <= n; i ++ )
    {
        st[i] = true;
        q.push(i);
    }

    while (q.size())
    {
        int t = q.front();
        q.pop();

        st[t] = false;

        for (int i = h[t]; i != -1; i = ne[i])
        {
            int j = e[i];
            if (dist[j] > dist[t] + w[i])
            {
                dist[j] = dist[t] + w[i];
                cnt[j] = cnt[t] + 1;

                if (cnt[j] >= n) return true;
                if (!st[j])
                {
                    q.push(j);
                    st[j] = true;
                }
            }
        }
    }

    return false;
}

int main()
{
    scanf("%d%d", &n, &m);

    memset(h, -1, sizeof h);

    while (m -- )
    {
        int a, b, c;
        scanf("%d%d%d", &a, &b, &c);
        add(a, b, c);
    }

    if (spfa()) puts("Yes");
    else puts("No");

    return 0;
}

1. dist数组的含义：现在不表示 x点到1号点的距离

表示的是：用于判断，如果有负边，则走；

这样的话，全都初始化为0，边值比0大则不管，比0小则走，

这样的话，如果有负环，那么就会一直走；如果仅仅是负边，而不是负环，一定不会一直走下去（代码就给限制住了）

2. 由于我们要遍历到所有边，那么我们就需要spfa算法中，把所有节点都入队列

因为spfa算法求1到n的最短路径的时候，只是把1节点先入队列

如果按着只把1节点入队列，那么如果不是连通图，就不能遍历到所有边

3. cnt数组的作用，cnt的角标 即表示 节点出现的次数，如果没有最短路径