文章目录
- 一、最小二乘法
- 1.最小二乘法
- 2.加权最小二乘法
- 3.递归最小二乘法
- 4.最小二乘法与极大似然
- 二、卡尔曼滤波
- 1.概述
- 2.线性卡尔曼滤波
- 3.扩展卡尔曼滤波
- Error State卡尔曼滤波
- 4.无迹卡尔曼滤波
- (1)无迹变换
- (2)无迹卡尔曼滤波
一、最小二乘法
1.最小二乘法
2.加权最小二乘法
3.递归最小二乘法
4.最小二乘法与极大似然
二、卡尔曼滤波
1.概述
卡尔曼滤波器与线性递归最小二乘滤波器非常相似。递归最小二乘可以更新参数的估计值,但卡尔曼滤波器却能够对状态量进行估计和更新。卡尔曼滤波器的目标是对该状态量进行概率估计,主要是分两步实时更新:预测和修正。
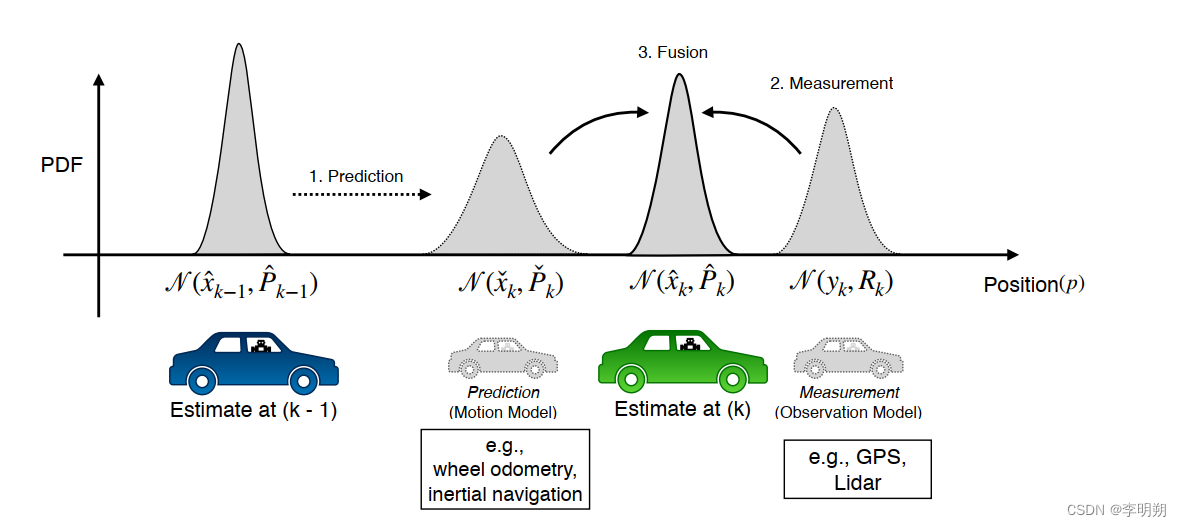
- 首先从时间 k − 1 时的初始概率估计开始,我们使用从车轮里程计或惯性传感器测量得出的数据使用运动模型来预测汽车的位置。
- 然后,我们使用从 GPS或Lidar 测量得出的数据并使用测量模型来修正 k 时刻汽车的位置。这里,我们可以将卡尔曼滤波器视为一种融合来自不同传感器的信息对未知状态进行最终估计的技术,并同时考虑到运动和测量模型中的不确定性。
2.线性卡尔曼滤波
首先定义汽车的运动模型
x
k
=
F
k
−
1
x
k
−
1
+
G
k
−
1
u
k
−
1
+
w
k
−
1
x_{k} = F_{k-1}x_{k-1}+G_{k-1}u_{k-1}+w_{k-1}
xk=Fk−1xk−1+Gk−1uk−1+wk−1
其中
F
k
−
1
\ F_{k-1}
Fk−1是系统状态转移矩阵,
G
k
−
1
\ G_{k-1}
Gk−1是系统控制矩阵,
u
k
\ u_{k}
uk是系统输入信号,
w
k
−
1
\ w_{k-1}
wk−1是过程噪声
之后定义测量模型
y
k
=
H
k
x
k
+
v
k
y_{k} = H_{k}x_{k}+v_{k}
yk=Hkxk+vk
其中
H
k
\ H_{k}
Hk是测量矩阵,
v
k
\ v_{k}
vk是测量噪声
卡尔曼滤波的过程如下:
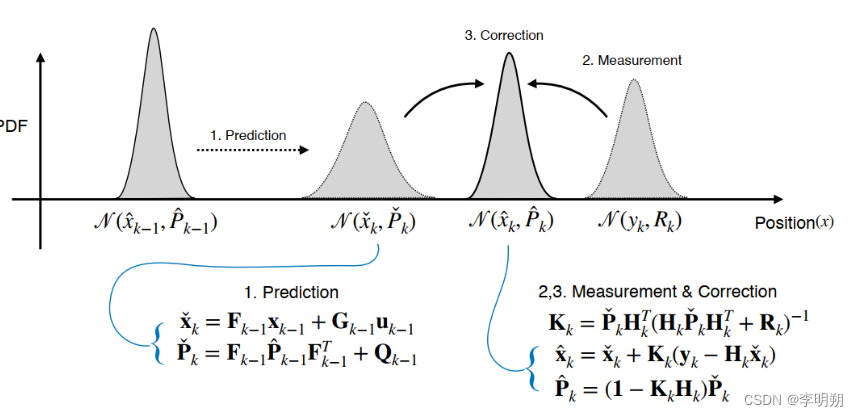
- 首先,我们使用运动模型来预测:
x ˇ k = F k − 1 x k − 1 + G k − 1 u k − 1 P ˇ k = F k − 1 P ^ k − 1 F k − 1 T + Q k − 1 \check{x} _{k} = F_{k-1}x_{k-1}+G_{k-1}u_{k-1}\\ \check{P}_{k}= F_{k-1}\hat{P}_{k-1}F_{k-1}^{T} +Q_{k-1} xˇk=Fk−1xk−1+Gk−1uk−1Pˇk=Fk−1P^k−1Fk−1T+Qk−1 - 然后,我们计算卡尔曼增益:
K k = P ˇ k H k T ( H k P ˇ k H k T + R k ) − 1 K_{k}=\check{P}_{k}H_{k}^{T}(H_{k}\check{P}_{k}H_{k}^{T}+{R}_{k})^{-1} Kk=PˇkHkT(HkPˇkHkT+Rk)−1 - 最后,修正系统状态量和协方差矩阵:
x ^ k = x ˇ k + K k ( y k − H k x ˇ k ) P ^ k = ( I − K k H k ) P ˇ k \hat{x} _{k} = \check{x} _{k}+K_{k}(y_{k}-H_{k}\check{x} _{k})\\ \hat{P} _{k} =(I-{K} _{k}{H} _{k})\check{P} _{k} x^k=xˇk+Kk(yk−Hkxˇk)P^k=(I−KkHk)Pˇk
在噪声期望为零则不相关的情况下,卡尔曼滤波器是无偏且一致的,即满足以下数学关系:
E
[
e
k
^
]
=
0
E
[
e
k
^
e
^
k
T
]
=
P
k
^
E[\hat{e_{k} } ] = 0 \\ E[\hat{e_{k}}\hat{e}_{k}^{T}] = \hat{P_{k}}
E[ek^]=0E[ek^e^kT]=Pk^
通常,如果我们有白色不相关的零期望噪声,则卡尔曼滤波器是最好的(即最低方差)无偏估计滤波器,它以最小的方差进行无偏估计。
3.扩展卡尔曼滤波
为了对非线性系统进行状态估计,我们将使用称作扩展卡尔曼滤波的状态估计算法。扩展卡尔曼滤波的关键是线性化非线性系统,这里需要用到泰勒展开式。泰勒展开后通常只保留一阶部分,略去高阶部分。
对于非线性系统运动模型和测量模型,我们需要对它们进行线性化处理。我们选择状态的最新估计值作为泰勒展开点,得到如下公式
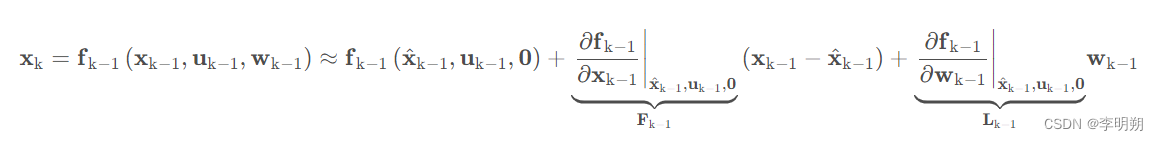
对于测量模型,线性化处理为:
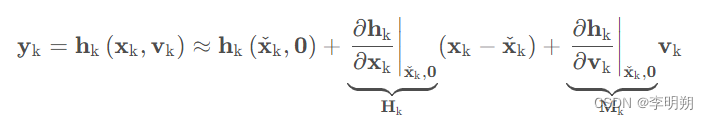
在以上公式中,
F
k
−
1
\ F_{k-1}
Fk−1,
L
k
−
1
\ L_{k-1}
Lk−1,
H
k
\ H_{k}
Hk,
M
k
\ M_{k}
Mk 被称为系统的Jacobian矩阵。Jacobian矩阵是一个包含所有一阶偏导数的矩阵。如下图所示:
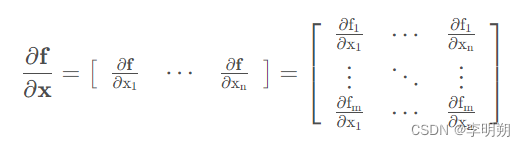
将它们代入我们的标准卡尔曼滤波器方程中,含有雅可比矩阵的扩展卡尔曼滤波器方程为:

Error State卡尔曼滤波
在ES-EKF中,我们将使用EKF估计误差状态,误差状态就是在任何给定时间名义状态(汽车估计位置)和真值状态(汽车真实位置)之间的差异,然后使用误差状态估计值修正名义状态。在运动模型和测量模型中误差状态表示如下:
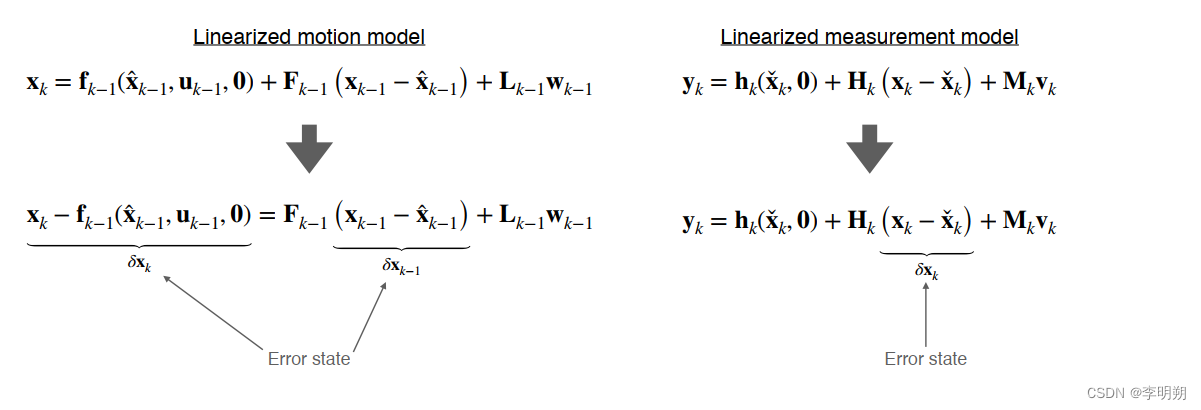
ES-EKF的处理方法如下:
- 首先使用非线性运动模型和当前状态的最佳估计来更新名义状态。
x k ˇ = f k − 1 ( x k − 1 , u k − 1 , 0 ) \check{x_{k}} =f_{k-1}(x_{k-1}, u_{k-1}, 0) xkˇ=fk−1(xk−1,uk−1,0) - 然后是预测协方差矩阵。
P k ˇ = F k − 1 P k − 1 F k − 1 T + L k − 1 Q k − 1 L k − 1 T \check{P_{k}} =F_{k-1}P_{k-1}F_{k-1}^{T}+L_{k-1}Q_{k-1}L_{k-1}^{T} Pkˇ=Fk−1Pk−1Fk−1T+Lk−1Qk−1Lk−1T - 当有新的测量值到来时,首先计算卡尔曼增益:
K k = P k ˇ H k T ( H k P k ˇ H k T + R ) − 1 K_{k}=\check{P_{k}}H_{k}^{T}(H_{k}\check{P_{k}}H_{k}^{T}+R)^{-1} Kk=PkˇHkT(HkPkˇHkT+R)−1 - 然后是计算误差状态。
δ x k ^ = K k ( y k − h k ( x k ˇ , 0 ) \delta \hat{x_{k}} =K_{k}(y_{k}-h_{k}(\check{x_{k}}, 0) δxk^=Kk(yk−hk(xkˇ,0) - 修正名义状态。
x k ^ = x k ˇ + δ x k ^ \hat{x_{k}} = \check{x_{k}}+\delta \hat{x_{k}} xk^=xkˇ+δxk^ - 最后更新协方差矩阵。
P k ^ = ( I − K k H k ) P k ˇ \hat{P_{k}} =(I-K_{k}H_{k})\check{P_{k}} Pk^=(I−KkHk)Pkˇ
EKF的使用限制:
- 容易产生线性化误差,特别时当系统运动模型和测量模型高度非线性时;或当传感器采样时间过慢时(与自动驾驶汽车速度相比),也会产生很大的线性化误差。
- 线性化误差很大时,会产生两个结果:一是估计值可能与真实值相差很大,二是估计协方差可能无法准确捕捉状态的真实不确定性,这会导致整个系统发散,而且通常很难再收敛回来。
- 在实践中最常见的问题是在计算雅可比矩阵时很容易出错,尤其是在处理复杂的非线性系统时。工程上也有人试图通过使用数值微分或在编译时使用自动微分来解决这个问题。但是这些都有自己的陷阱,有时会表现得不可预测。
4.无迹卡尔曼滤波
(1)无迹变换
无迹变换的背后思想是:近似概率分布比近似任意非线性函数更容易。无迹变换的基本思想分为三个步骤。
- 首先,我们从输入分布中选择一组样本点。这些不是随机样本,它们是确定性样本,它们被选择为远离平均值一定数量的标准差。出于这个原因,这些样本被称为 sigma points。
- 第二个步骤是将每个 sigma point 通过非线性函数,产生一组属于输出分布的新sigma point。
- 最后,我们可以使用一些精心选择的权重来计算输出 sigma points的样本均值和协方差,这将使我们能够很好地近似真实输出分布的均值和协方差。
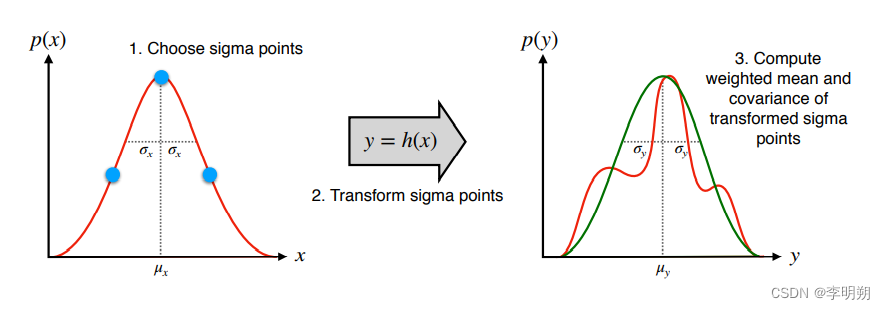
这其中有两个重要步骤,分别是
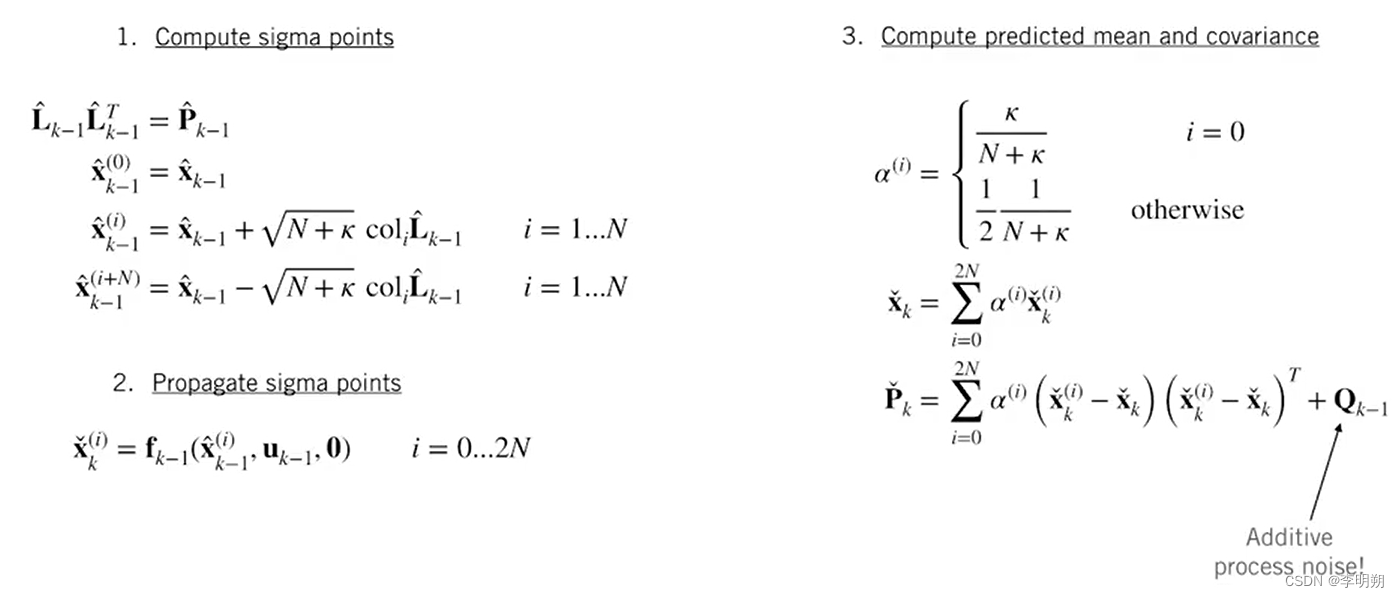
- 选取sigma point:通常,对于n nn维概率分布,我们需要 2 n + 1 2n+12n+1 个 sigma point,一个为均值,其余关于均值对称分布。选取 sigma point 的第一步是对输入分布的协方差矩阵进行 Cholesky分解,我们就可以选择分布均值作为第一个 sigma point,其余 sigma point 的选择可以用图中的公式来实现。其中 κ参数一般取值为3,N为维度。

- 计算均值和方差:首先通过非线性函数得到一组新的sigma point,之后通过这些点计算均值和方差,如下图所示

(2)无迹卡尔曼滤波
无迹卡尔曼滤波主要思想是:使用无损变换来直接逼近概率分布函数。
首先是预测步,主要包含三步:选取sigma point;非线性转换;计算新的均值和方差
之后是修正步,主要包含四步,分别是计算预测测量;计算预测测量的均值和方差;计算卡尔曼增益;计算修正后的均值和方差

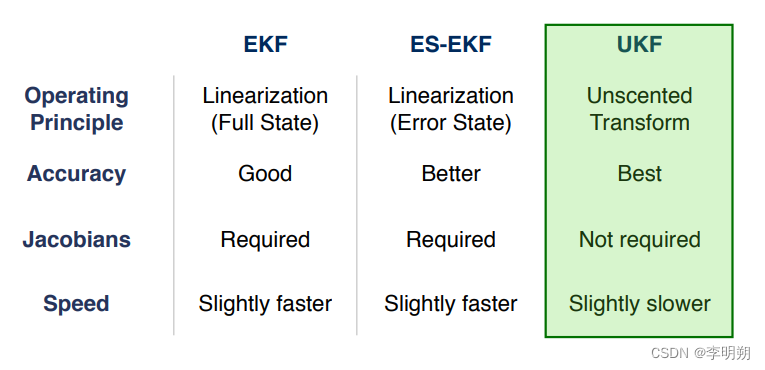
综上所述,三种卡尔曼滤波器的主要区别在于 EKF 依靠局部分析线性化来通过非线性函数传播 PDF,无论是EKF 还是 ES-EKF。相比之下,UKF 依靠无损变换来处理非线性函数。三者对比如下表示所示。