Karush-Kuhn-Tucker (KKT)条件
〇、问题背景
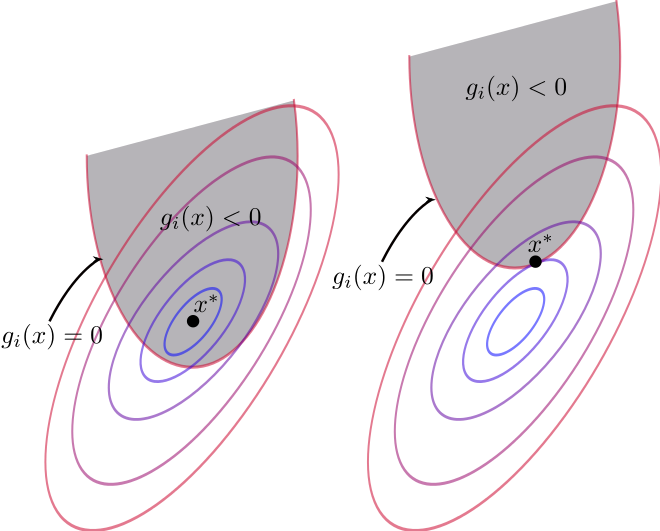
在阅读 Karush-Kuhn-Tucker (KKT)条件 时,不太能理解 ∇ f \nabla f ∇f 的方向,以及 ∇ g \nabla g ∇g 的方向:
为什么 ∇ f \nabla f ∇f 是指向可行域内部, ∇ g \nabla g ∇g 指向可行域外部?

一、首先,弄明白 ∇ \nabla ∇ 梯度 的定义:
梯度的定义可以简单地表示为:梯度是一个向量,它指向函数值增长最快的方向,并且其模长等于增长率。
二、开始分析
对于 f f f,无约束最小值在中心(左),而 ∇ f \nabla f ∇f 指向函数值增长最快的方向,所以是远离 中心(最小值) 的方向,即:可行域内部。
对于 g g g,因为内部是 ≤ 0 ≤0 ≤0、外部是 > 0 >0 >0, ∇ g \nabla g ∇g 指向函数值增长最快的方向,所以肯定是往外部的方向。
∇ f \nabla f ∇f 与 ∇ g \nabla g ∇g 反向
三、实战
例1
“ 如果我们要最大化 f ( x ) f(x) f(x) 且受限于 g ( x ) ≤ 0 g(x) ≤ 0 g(x)≤0,那么对偶可行性要改成 λ ≤ 0 \lambda ≤ 0 λ≤0 ”。
—— Karush-Kuhn-Tucker (KKT)条件
对于 ∇ f \nabla f ∇f:指向可行域外部(无约束最大值在中心,指向中心,即:可行域外部)。
对于 ∇ g \nabla g ∇g:指向可行域外部
∇ f \nabla f ∇f 与 ∇ g \nabla g ∇g 同向
∵ 满足:
∇
f
=
−
λ
∇
g
\nabla f = -\lambda \nabla g
∇f=−λ∇g
∴
λ
≤
0
\lambda ≤ 0
λ≤0
例2:经典SVM
原始问题和约束条件:
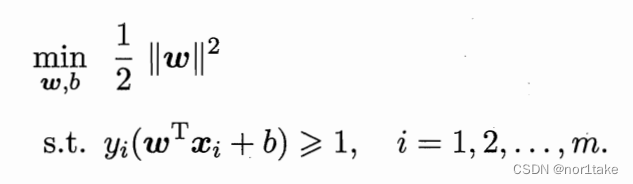
注意:
g
(
x
)
=
1
−
y
i
(
w
T
x
i
+
b
)
≤
0
g(x) = 1- y_i(w^Tx_i+b) ≤ 0
g(x)=1−yi(wTxi+b)≤0,
α
i
≥
0
\alpha_i ≥ 0
αi≥0
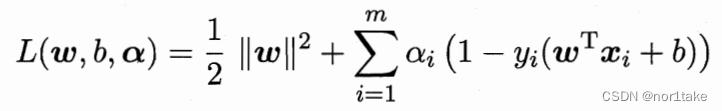



![[论文分享]TimeMAE:解耦掩码自编码器时间序列的自监督表示](https://img-blog.csdnimg.cn/7817ff7c6fb9426183c8d389d74de7fd.png)