【用人话讲算法】leetcode无重复字符的最长子串

文章目录

【用人话讲算法】leetcode无重复字符的最长子串
- 题目
- 简单思路（暴力）
- 优化思考
- 怎么写代码？怎么到下一个？
- - while
  - for
- 思路总结
- while和for循环总结

题目

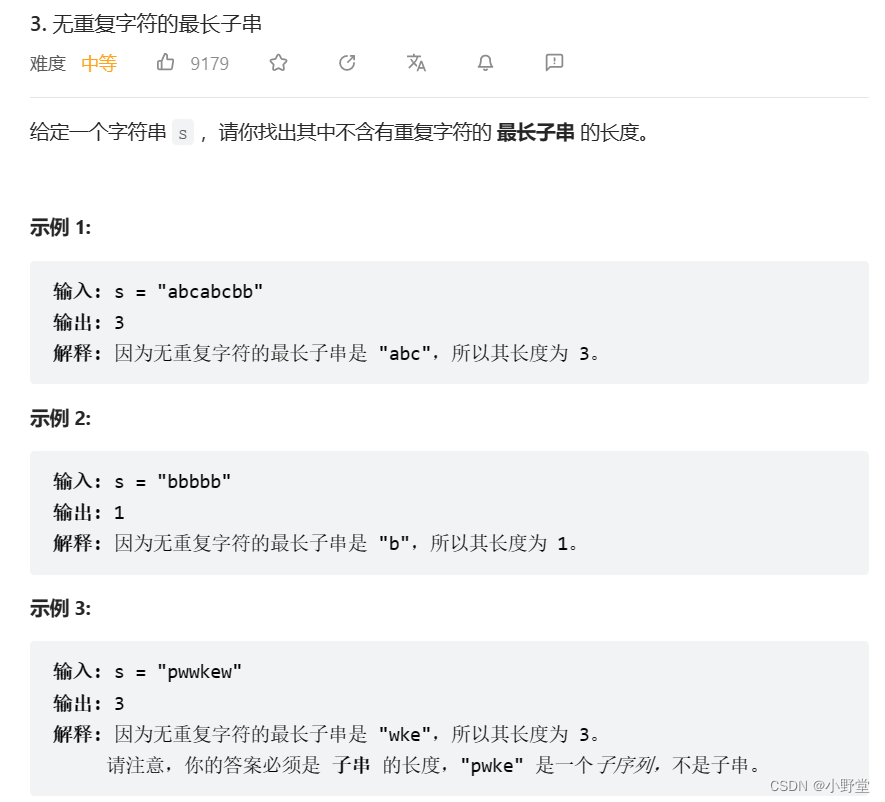
在这里插入图片描述
题目的意思是说，从一串字符中找到一个子字符串，这个子字符串中的字符需要全部都是不相同的，求解这样的字符串中，长度最长的那个子字符串的长度是多少。

简单思路（暴力）

我们先想想，作为人类，我们会怎么解决这个问题。
首先因为并不能确定这个子字符串是从哪里开头的，因此我们会从每个字符都开头一次，试一试。当碰到一个字符和已经存在的串里面的数字相同的时候，我们就可以知道当这个数字开头的时候，最长的长度是多少，接着就可以比较所有数字开头的时候找到的最大的串里面最大的，我们就可以知道这个最长的子串的长度了。

优化思考

但是这样的解法是最优解吗？时间复杂度是O(n2)。需要回答这个问题，我们需要看看有没有哪些工作是可以不做的。

比如这样一个串：abcdeab
当a作为开头的字母的时候，我们会找到这样的串，
abcde然后换为b开头，我们找到的串为
bcdea，找这两个串的时候，比较每个数字的时候，过程其实是一模一样的，有没有什么办法可以记录下来这样的事情？

作为人类我们可以想到如下的办法：
在这里插入图片描述
看起来也很有道理是不是！但是怎么让计算机知道呢？
也许我们可以把这个子串记录下来，毕竟我们总是在拿空间换时间的。然后当我们指到下一个的时候，只要在记录里面，我们就在这个记录里面删除前面那些数字，直到找到那个切断的数字之后，切断前面的，就可以继续的往后找了。

上面的过程是不是就和我们人的思维很接近了？看起来是不是也没有重复做功？

但是仔细的思考看看就会发现，我们人在找这个切断的时候，是通过眼睛完成的！但是如果机器需要通过遍历才能找到的话，还是需要在里面再重复一遍，因此复杂度不一定可以降下来。[苦涩]

这个时候我们灵机一动，想起来了在leetcode两数相加中学习到的一个数据结构，哈希表！哈希表同学可以帮助我们在一堆数中，用O(1)的复杂度就找到对应的数字，这个和人的定睛一看，异曲同工之妙啊。剩下的问题就是，怎么定位到切除点了。我们可以发现切除点一定是顺着进行的，因此可以设置一个在前面的指针，记录上一个切除点的位置，当遇到和后面进行的指针

怎么写代码？怎么到下一个？

需要在中间处理用的过程的数据和处理的步骤都思考好了，开始写代码！猛然发现，还有一个问题没有处理就是，怎么让一切进行啊~简单的思考是，用while和for都可以。但是从思考来说，其实for可能更简单一些，下面来看看用for和while的时候，脑子思考的都是什么东西，写出来的代码是什么样子的。脑子思考的东西我放在代码注释里面，解释的超级清楚！

while

用while的时候其实需要思考的东西相对的多些，需要想清楚进入的判断条件是什么，需要思考清楚循环内会怎么修改这个数字，以及是不是能够没有问题的退出循环。在循环退出之后，思考退出之后得到的数字都是怎么样子的，还需要怎么处理以及返回值是什么样子的。

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if len(s) < 2: return len(s)
        record = set()
        left, right = 0 , 0  # 左右边界，左闭右闭
        record.add(s[left])  
        maxLength = 1  # 目前的集合的长度
        while right <= len(s) - 2:  # 当集合的右边还是有数的时候，即可以继续往后一个
            if s[right+1] not in record:  # 可以继续往右边挪的情况
                record.add(s[right+1])
                right += 1
                continue
            maxLength = max(maxLength,len(record)) # 挪不了了找到了一个子串
            while s[right+1] in record:  # 寻找截断点
                record.remove(s[left])
                left += 1  # 表示集合的最前面数字的index
        return max(maxLength,len(record))

这里我们进入循环的条件是，右边没有到最后（因此前面写了长度小于2的时候，是不满足这个情况的），并且在循环内每次最多只会对于右边挪动一个位置。因此最终结束的时候，右边一定到了最后的，但是左边是不能确定的，record里面都可能是有数的，并且这个时候的长度是没有和maxLength进行过比较的，因此返回两者中的较大值即可。

为什么这样的算法可以时间复杂度是O(n）呢？因为我们发现我们挪动的只有左右，且不会往回移动，因此最多就是全部走一遍，就是O(n)（因为中间的判断需不需要截断的部分，我们用哈希表做到了时间复杂度为O(1)）。

for

同时，我们也发现，整个过程中，挪动的结束的时候，右边一定是在最后的，因此也可以拿这个来控制。

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if len(s) < 2: return len(s)
        left = 0
        record = {s[left]}
        maxLength = 1
        for i in range(1,len(s)): # 控制右边界的右边元素
            if s[i] not in record:
                record.add(s[i])
                continue
            maxLength = max(maxLength,len(record))
            while s[i] in record:
                record.remove(s[left])
                left += 1
            if s[i] not in record: record.add(s[i])
        return max(maxLength,len(record))

这个地方需要注意的是，每个循环内，右边一定都会往右边挪一个。因此，每个循环内需要完成的所有工作，包括把挪之前的右边加进去，也需要考虑到，要在这个循环内完成。

也可以考虑控制左边来写，写出来的代码如下：

class Solution:
    def lengthOfLongestSubstring(self, s: str) -> int:
        if len(s) <2 :return len(s)
        maxLength, right = 0,0
        record = set()
        for i in range(len(s)):
            if i != 0:
                record.remove(s[i-1])
            while (right<len(s)) and (s[right] not in record):
                record.add(s[right])
                right += 1
            maxLength = max(maxLength,len(record))
        return maxLength