在几何里可分为两种几何,一种是显式几何,另外一种是隐式几何。有不同的方式表示不同的几何
隐式几何
隐式实际上是说不会告诉具体的这些点点就在哪,只告诉你这些点满足的关系。表示一定的关系但并不会给实际的点
例子:

隐式几何表示方式
缺点光从上面的公式很难看出表示的几何形状
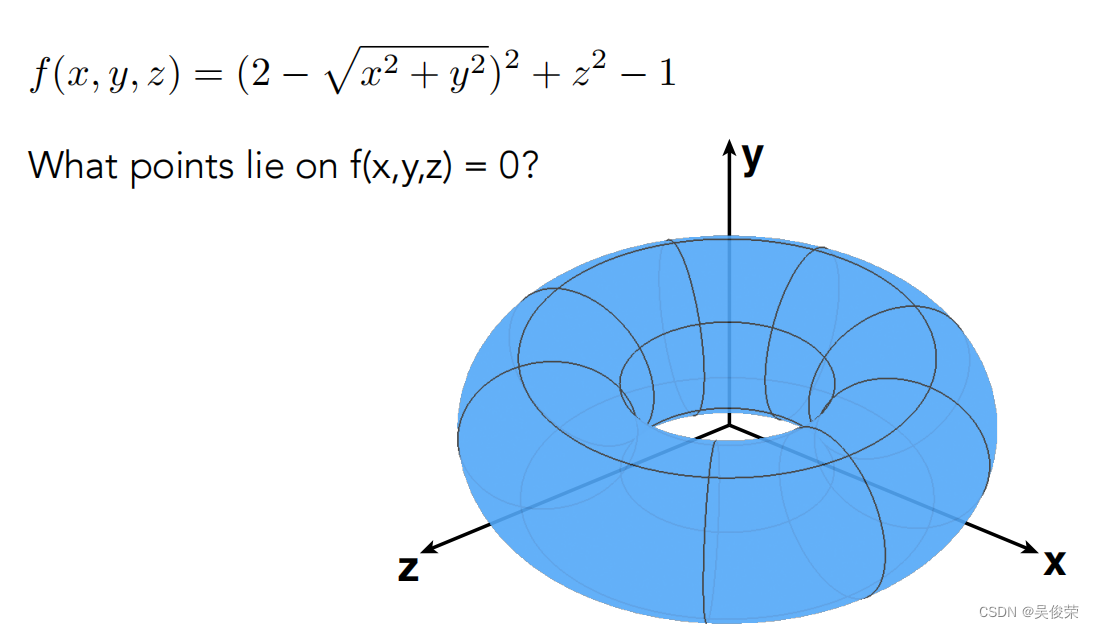
优点是能判断一个点在不在这个几何上
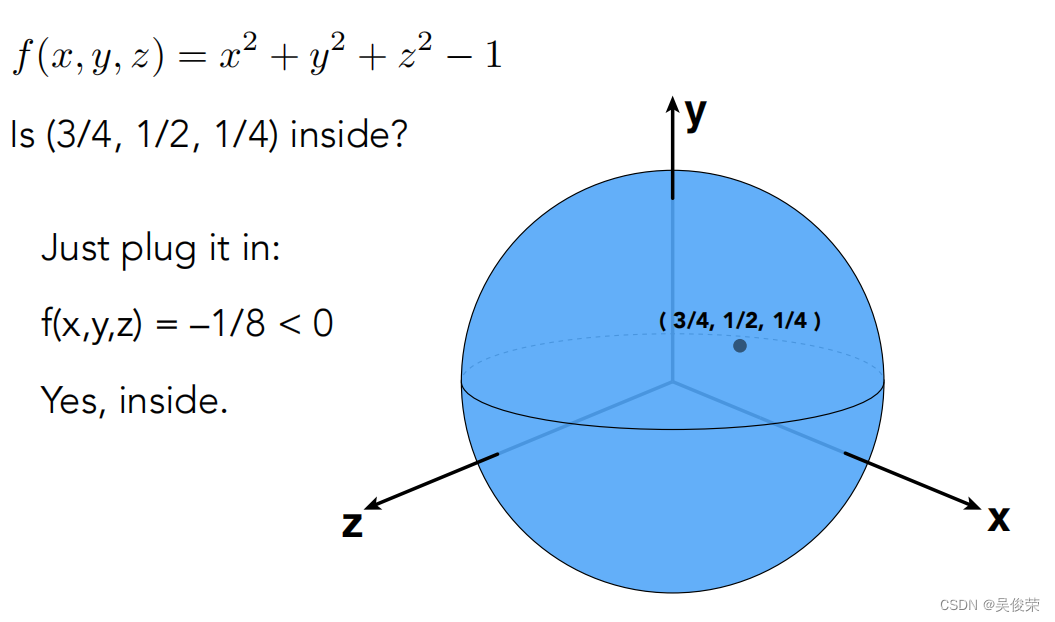
显式几何
显式是一个三角面直接用点表示出来,还有一个是通过参数映射的方法定义的表面,比如
输入的UV映射到空间中某一个点,定义一个函数给你的是UV 输出的是(x,y,z)
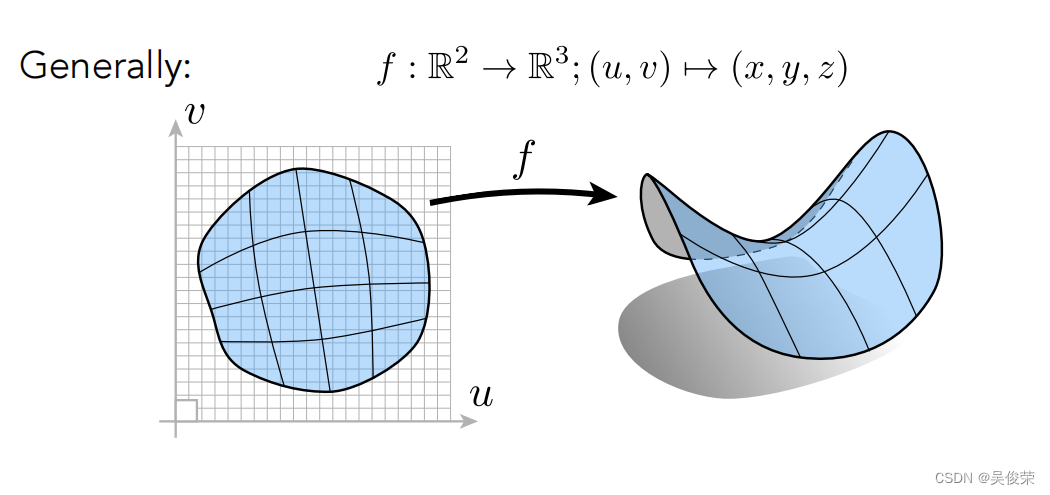
例子
把UV映射成了空间中实际的点(x,y,z),
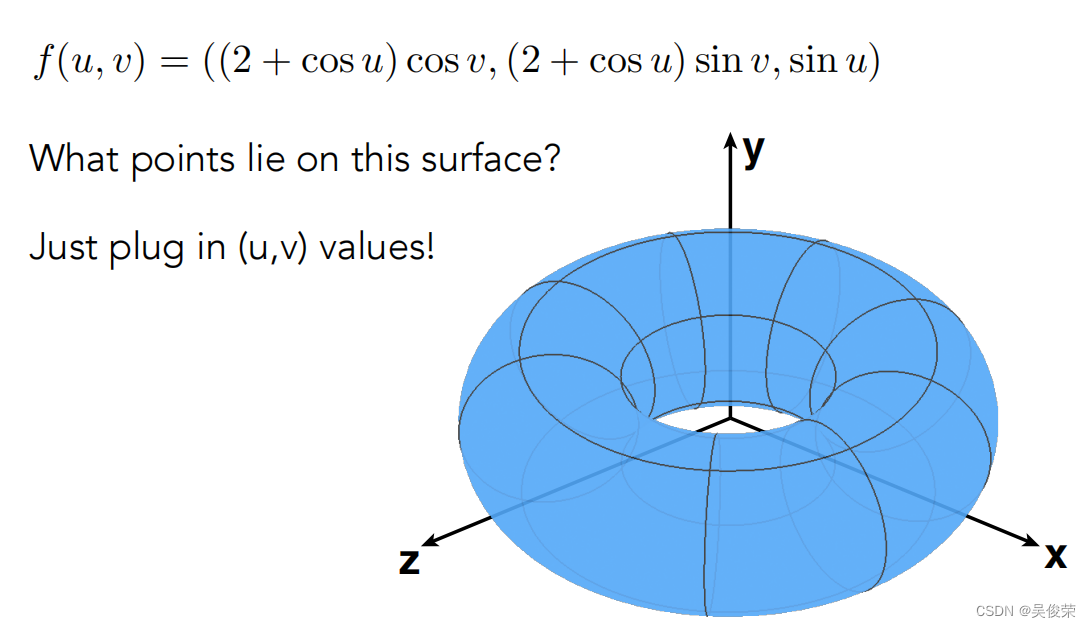
想判断一个点在不在几何上变的很难
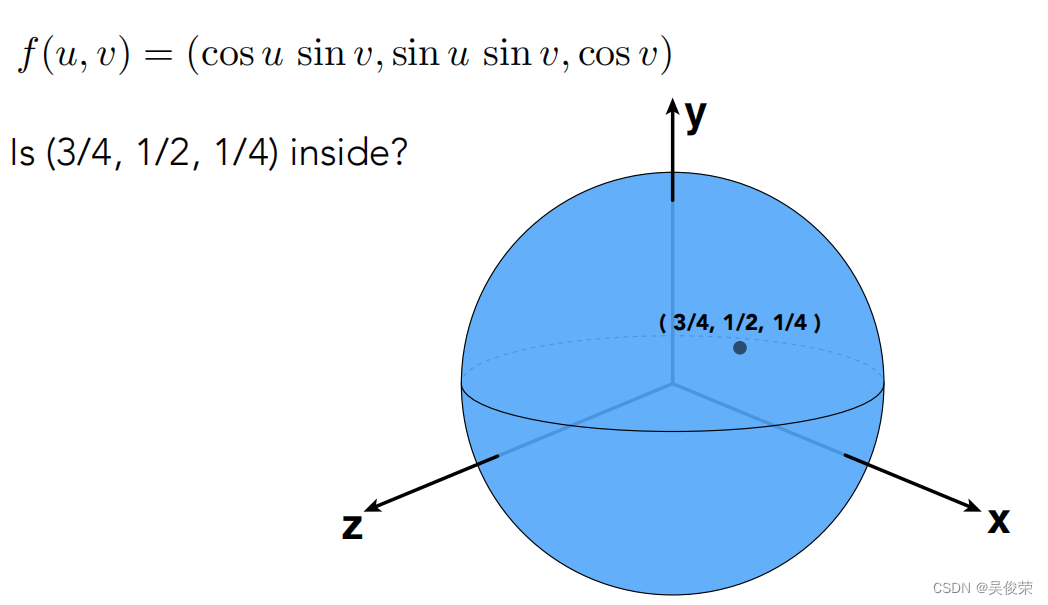
隐式几何的一些应用
通过一些简单布尔的运算形成一个复杂的几何
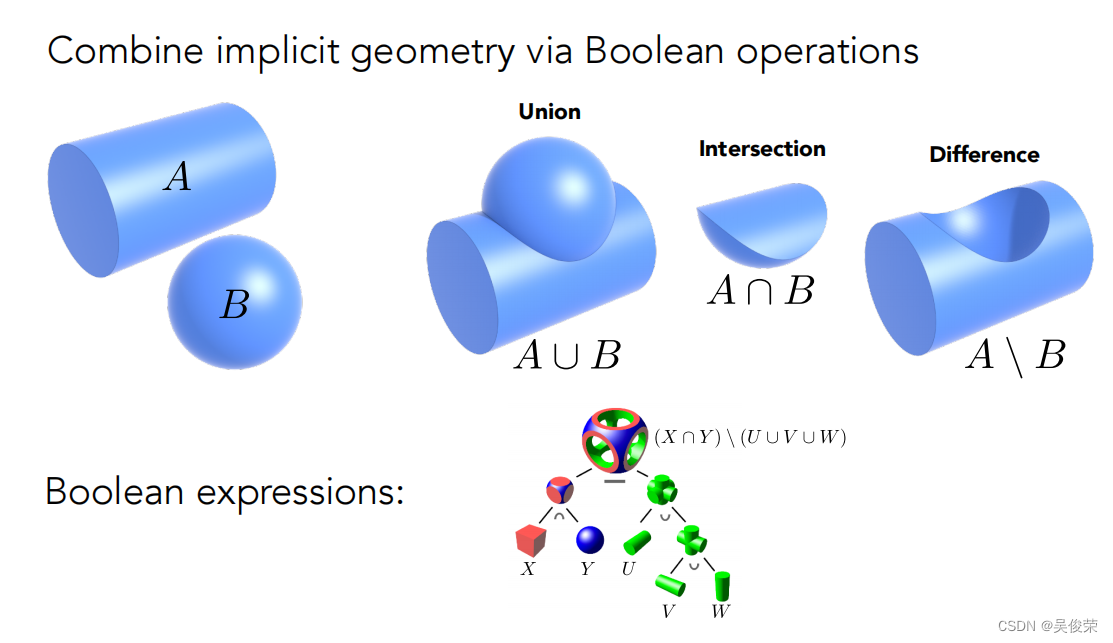
通过距离函数运算
对于任何一个几何,都不直接描述它的表面,去描述它的任何一个点到这个表面的最近的距离。
通过对几何的距离函数做融合形成的结果
距离函数是指空间中任何一个点到你想要表示的几何形体上的任意一个点它们之间最小的距离,这个距离可以是正的或者负的,如果认为有一个点在几何表面外面,那这个点的最小距离算出来之后加个正号,那就是正的,如果有一个点在几何内部那,那这个点到这个几何的表面上的最小距离,并且认为这个距离是负的。也就说把空间中任何一个点都定义出一个值来,把两物体的距离函数都算出来之后,然后把两个距离函数做一个融合,然后在恢复成原来的物体就可以得到下面的变换了

一个应用距离函数的例子
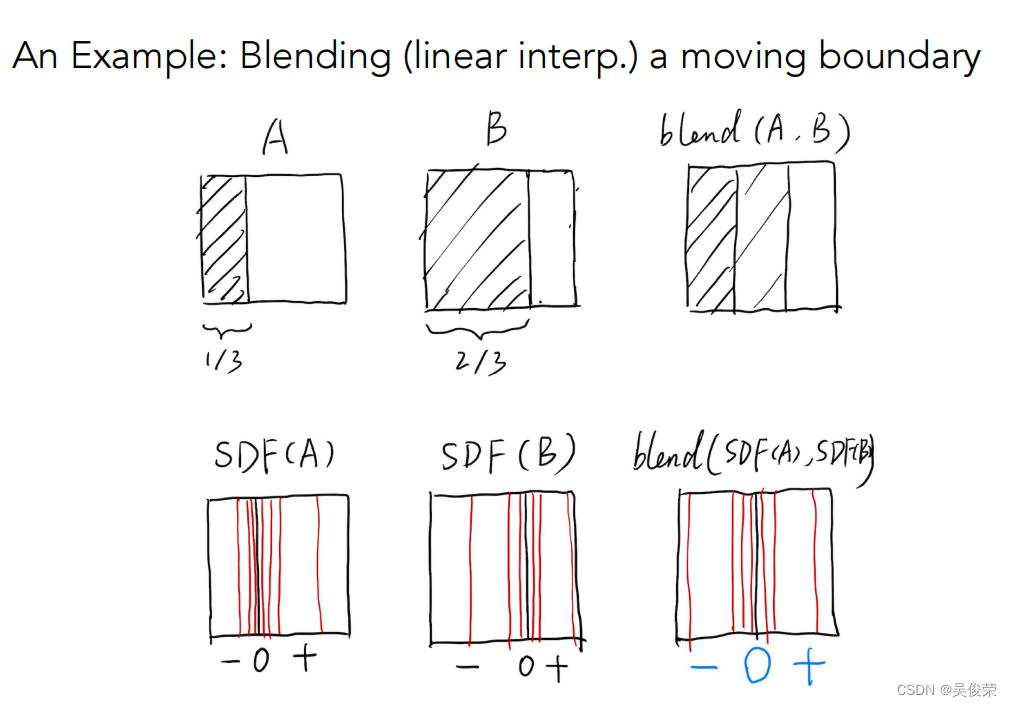
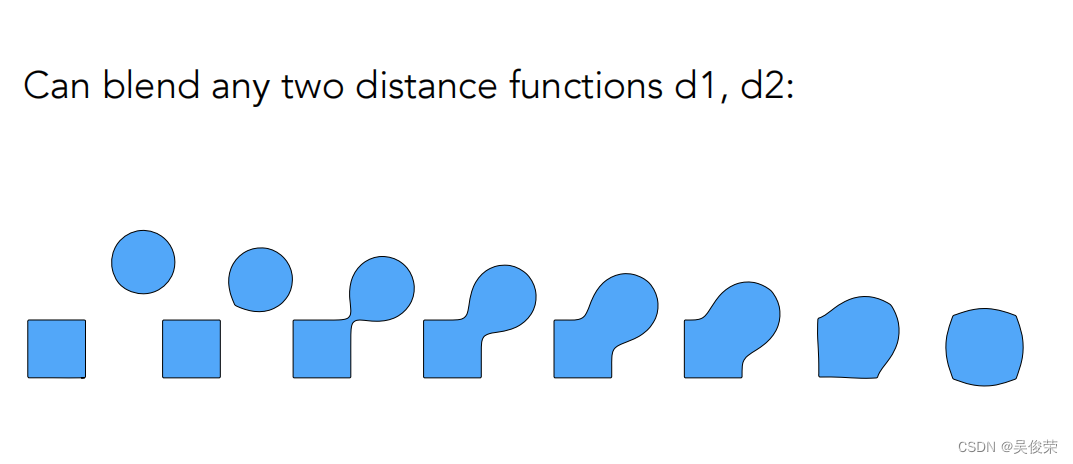
距离函数实际的例子
 距离函数出来融合后怎么恢复成表面
距离函数出来融合后怎么恢复成表面
把距离函数等于0的全部找出来其实很难找出来
替代方法:存储函数近似值的网格(水平集)
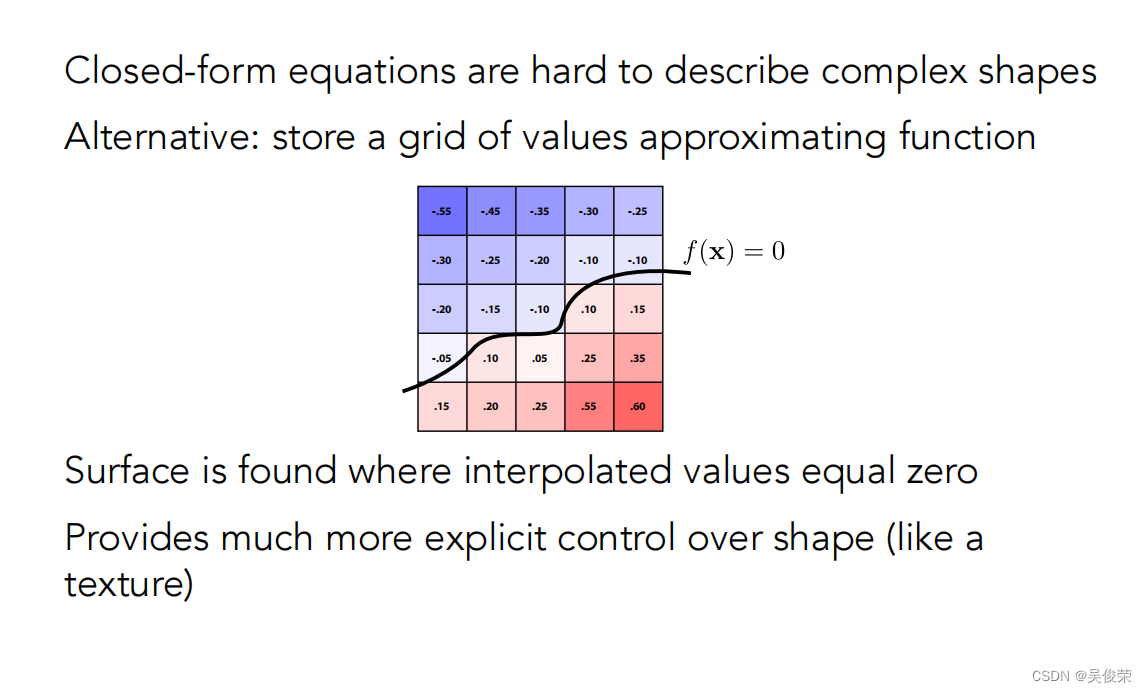
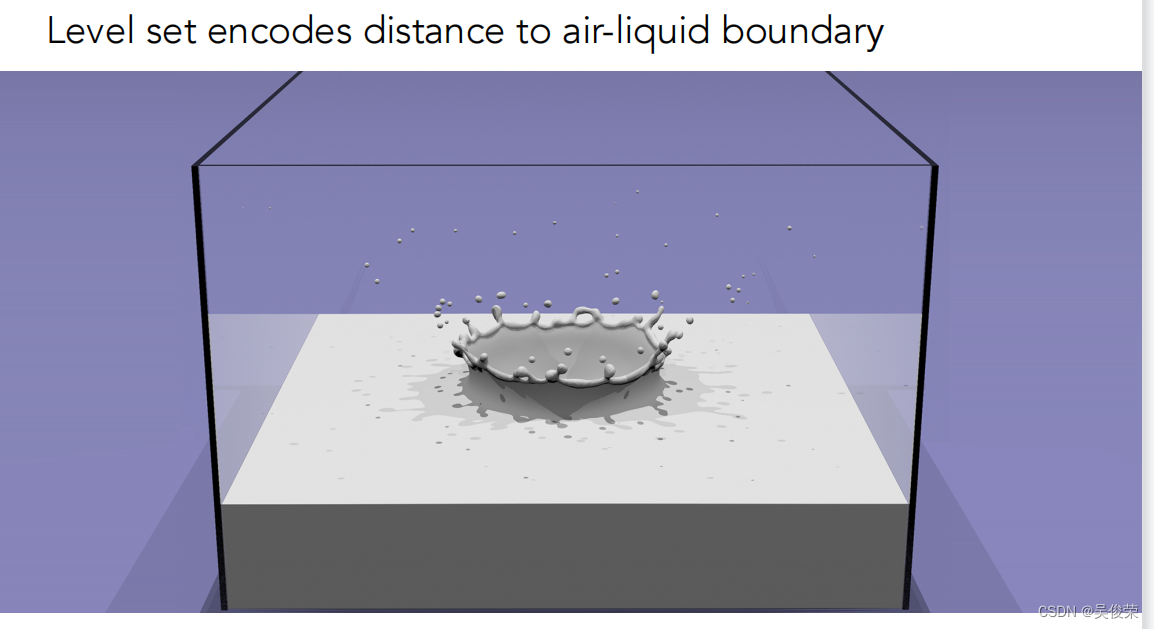
水平集不一定定义在二维也可以定义在三维

还有一种特殊的描述方法Fractals(分形)
分形是指似相似的意思,是自己的一部份和自己长的非常像,类似于递归

显式几何的一些应用

点云
不考虑物体是一个表面,而是表面上的一堆点,把每一个点都表示成一个点,只要这些点表示的足够细,自然就看不打点于点之间的缝隙,做一些三维空间的扫描

多边形网格
比较常用的,比如三维建模软件