【最长上升子序列】、【最长公共子序列】、【最长公共上升子序列】
- 最长上升子序列
- f[i] 表示以i结尾的最长子序列
- 最长公共子序列
- f[i][j] 表示 a前i 和 b前j个 最长公共长度
- 最长公共上升子序列
- f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
- 最长公共子串
最长上升子序列
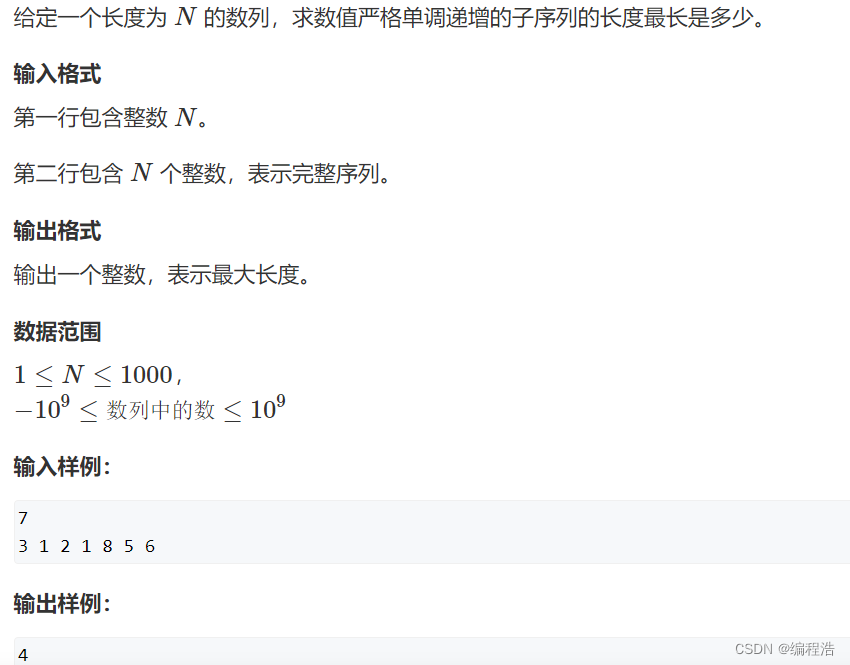
f[i] 表示以i结尾的最长子序列
由于我们遍历到i时候
我们需要比较i前面的数据
我们发现如果i 大于 j
那么i就可以拼接在 j 后面
如果f[j] 就是j最长的了
那就
f[i] = f[j] + 1的长度
所以
f[i] 表示以i结尾的最长子序列
#include<iostream>
using namespace std;
const int N = 1100;
int a[N];
int f[N];
int res = 0;
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
a[0] = -0x3f3f3f3f;
for(int i = 1; i <= n; i++)
{
for(int j = 0; j <= i ; j++)
{
if(a[j] < a[i])
f[i] = max(f[i],f[j]+1);
res = max(res,f[i]);
}
}
cout << res;
return 0;
}
最长公共子序列

f[i][j] 表示 a前i 和 b前j个 最长公共长度
#include<iostream>
using namespace std;
const int N = 1010;
int f[N][N];
char a[N],b[N];
int n,m;
int main()
{
cin >> n >> m;
cin >> a+1 >> b+1;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
if(a[i]==b[j])
{
f[i][j] = f[i-1][j-1]+1;
}
else
{
f[i][j] = max(f[i-1][j],f[i][j-1]);
}
}
}
cout << f[n][m];
return 0;
}
最长公共上升子序列
f[i][j]代表所有a[1 ~ i]和b[1 ~ j]中以b[j]结尾的公共上升子序列的集合
这道题如何理解?
- 记住f[i][j] 表示什么
- 当b的j和i 相等时,我们常规思路是就在b数组中按着第一道题的逻辑 循环遍历之前的值,但是这样是麻烦的。我们需要一种方法,不需要遍历就知道之前的最大值,可以定义一个变量maxv,如果i和j相等,直接等于maxv,如果不相等,那么f[i][j] = f[i-1][j]
- 如果a[i]>b[j]
那么maxv = max(maxv,f[i-1][j]+1);
maxv的由来

#include<iostream>
using namespace std;
const int N = 3030;
int f[N][N];
int a[N],b[N];
int n;
int main()
{
cin >> n;
for(int i = 1; i <= n; i++) cin >> a[i];
for(int i = 1; i <= n; i++) cin >> b[i];
for(int i = 1; i <= n; i++)
{
int maxv = 1;
for(int j = 1; j <= n; j++)
{
f[i][j] = f[i-1][j];
if(a[i]==b[j])
{
f[i][j] = maxv;
}
if(a[i]>b[j])
maxv = max(maxv,f[i-1][j]+1);
}
}
int ans = 0;
for(int i = 0; i <= n; i++)
{
ans = max(f[n][i],ans);
}
cout << ans;
return 0;
}
最长公共子串

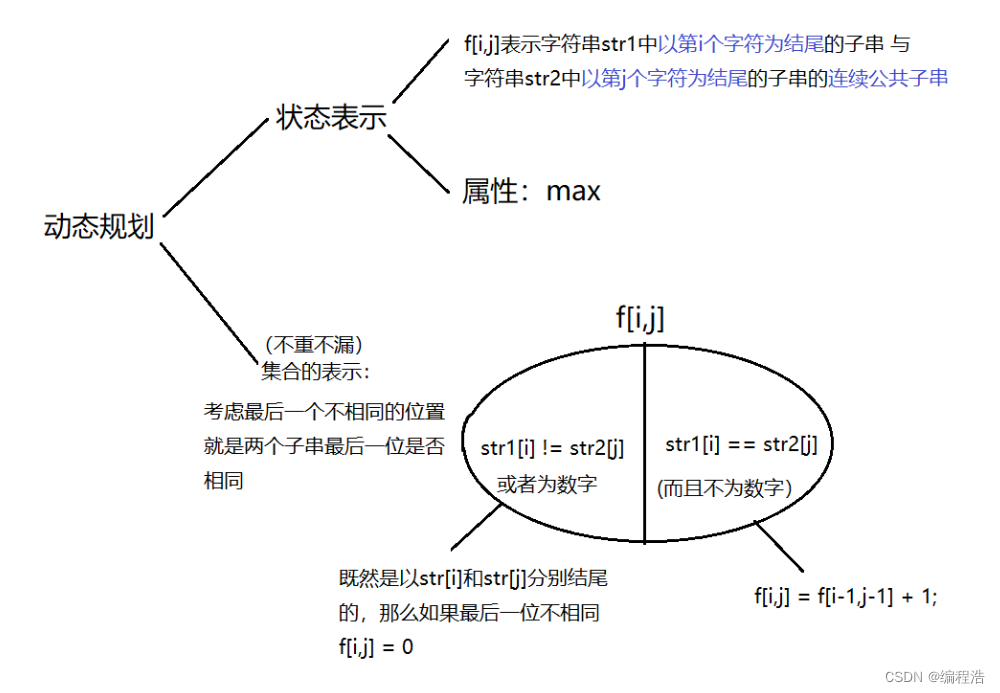
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
char str1[N], str2[N];
int f[N][N];//注意空间限制为256MB,即为2^(8 + 20) = 2^28个字节,
//而一个int型变量占4个字节,那么最多有2^26个int变量,大约为64000000个变量,而此时定义f[N][N]最多有大于1e8个变量,会爆内存
//更何况还有存字符串的空间
int main()
{
cin >> str1 + 1 >> str2 + 1;
int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);
int res = 0;
for (int i = 1; i <= len1; i++)
{
//如果最后一位为数字
if (str1[i] >= '0' && str1[i] <= '9')
{
for (int j = 1; j <= len2; j++)
f[i][j] = 0;
continue;
}
for (int j = 1; j <= len2; j++)
{
//如果最后一位相同且不为数字
if (str1[i] == str2[j])
f[i][j] = f[i - 1][j - 1] + 1;
else f[i][j] = 0;
res = max(res, f[i][j]);
}
}
cout << res << endl;
return 0;
}
观察我们在状态计算的过程,第i层循环的值,仅与第i-1层循环的值有关
我们可以联想到01背包的优化,利用滚动数组来简化空间复杂度
既然要用到删除一维空间的优化方法,一定要注意:
二维中:f[i][j] = f[i - 1][j - 1] + 1;
在一维中,由于f[j] = f[j - 1],小的j已经被更新,那么就不是上一层(i-1)的数据了
所以必须从大到小遍历
#include <iostream>
#include <cstring>
using namespace std;
const int N = 1e4 + 10;
char str1[N], str2[N];
int f[N];
int main()
{
cin >> str1 + 1 >> str2 + 1;
int len1 = strlen(str1 + 1), len2 = strlen(str2 + 1);
int res = 0;//用于保存答案
for (int i = 1; i <= len1; i++)
{
//如果最后一位为数字
if (str1[i] >= '0' && str1[i] <= '9')
{
for (int j = 1; j <= len2; j++)
f[j] = 0;
continue;
}
for (int j = len2; j >= 1; j--)
{
//如果最后一位相同且不为数字
if (str1[i] == str2[j])
f[j] = f[j - 1] + 1;
else f[j] = 0;
res = max(res, f[j]);
}
}
cout << res << endl;
return 0;
}