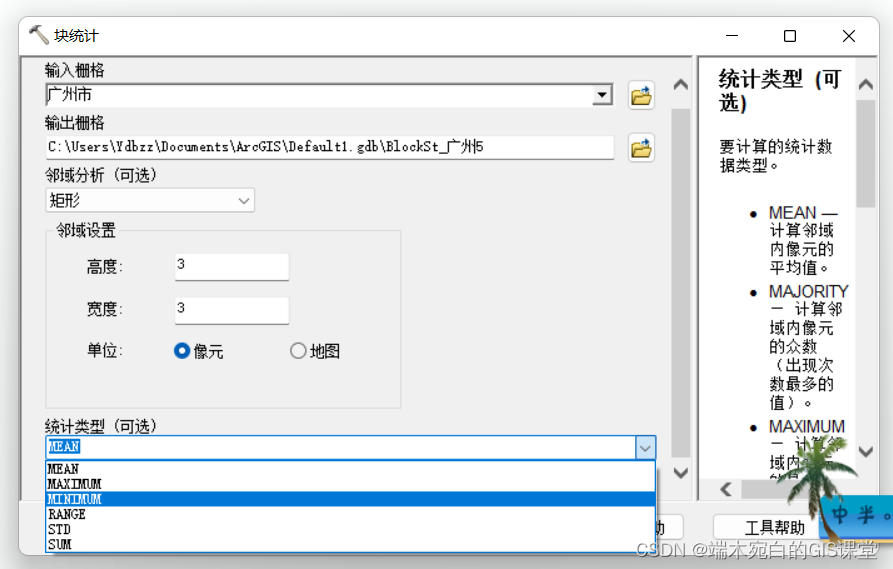
六大排序算法:插入排序、希尔排序、选择排序、冒泡排序、堆排序、快速排序
- 一、插入排序
- 二、选择排序
- 三、冒泡排序
- 四、归并排序
一、插入排序
1.从第一个元素开始,该元素可以认为已经被排序
2.取下一个元素tem,从已排序的元素序列从后往前扫描
3.如果该元素大于tem,则将该元素移到下一位
4.重复步骤3,直到找到已排序元素中小于等于tem的元素
5.tem插入到该元素的后面,如果已排序所有元素都大于tem,则将tem插入到下标为0的位置
6.重复步骤2~5
动画效果如下:

思路:
在待排序的元素中,假设前n-1个元素已有序,现将第n个元素插入到前面已经排好的序列中,使得前n个元素有序。按照此法对所有元素进行插入,直到整个序列有序。
但我们并不能确定待排元素中究竟哪一部分是有序的,所以我们一开始只能认为第一个元素是有序的,依次将其后面的元素插入到这个有序序列中来,直到整个序列有序为止。
c++代码演示如下:
void InsertSort(int* arr, int n)
{
//这是待插入的元素下标
for (int i = 1; i < n; i++)
{
//这是已经排序好数组的下标
for (int j = i - 1; j >= 0; j--)
{
//如果待排序数字大于,则向后移动
if (arr[j] > arr[j + 1])
{
int temp = arr[j];
arr[j] = arr[j + 1];
arr[j + 1] = temp;
}
else
{
break;
}
}
}
//排序结果输出
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
}
时间复杂度:最坏情况下为O(N*N),此时待排序列为逆序,或者说接近逆序;最好情况下为O(N),此时待排序列为升序,或者说接近升序。
空间复杂度:O(1)
二、选择排序
思路:每次从待排序列中选出一个最小值,然后放在序列的起始位置,直到全部待排数据排完即可。
实际上,我们可以一趟选出两个值,一个最大值一个最小值,然后将其放在序列开头和末尾,这样可以使选择排序的效率快一倍。
动画效果如下:

c++代码实现:
void SelectSort(int* arr, int n)
{
//开始从第一个元素进行选择排序
for (int i = 0; i < n-1; i++)
{
//最小值下标暂存变量
int min = i;
//依次从待排序区域取出数据与准备排序的数据进行比较,并暂存最小值下标
for (int j = i+1; j < n; j++)
{
//如果大于,则设置暂存变量
if (arr[min] > arr[j])
{
min = j;
}
}
//与找到的最小值下标互换数据
int temp = arr[i];
arr[i] = arr[min];
arr[min] = temp;
}
//排序结果输出
for (int i = 0; i < n; i++)
{
cout << arr[i] << " ";
}
}
时间复杂度:最坏情况:O(N^2)
最好情况:O(N^2)
空间复杂度:O(1)
三、冒泡排序
思路:
左边大于右边交换一趟排下来最大的在右边。以此类推。
动图如下:

c++代码如下:
void BubbleSort(int * arr, int len)
{
//如果数组为空或者只有一个数组,则返回
if (arr == NULL || len<2)
{
return;
}
//记录是否存在交换,如果不存在,则说明数组已经有序,直接退出,结束排序
bool flag = false;
//如果有两个以上的元素时,则开始排序
//循环外圈
for (int i = len ; i > 0; i--)
{
for (int j = 0; j < len; j++)
{
//如果大于,则交换
if (arr[j] > arr[j+1])
{
arr[j + 1] = arr[j + 1] ^ arr[j];
arr[j] = arr[j + 1] ^ arr[j];
arr[j + 1] = arr[j + 1] ^ arr[j];
flag = true;
}
}
if (!flag)
break;
else
flag = false;
}
//显示排序结果
for (int i = 0; i < len; i++)
{
cout << arr[i] << endl;
}
}
时间复杂度:最坏情况:O(N^2)
最好情况:O(N)
空间复杂度:O(1)
四、归并排序
思路:
1、首先将数组进行拆分