🔥 本文由 程序喵正在路上 原创，CSDN首发！
💖 系列专栏：数据结构与算法
🌠 首发时间：2022年12月4日
🦋 欢迎关注🖱点赞👍收藏🌟留言🐾
🌟 一以贯之的努力 不得懈怠的人生

有向无环图描述表达式

有向无环图（DAG）

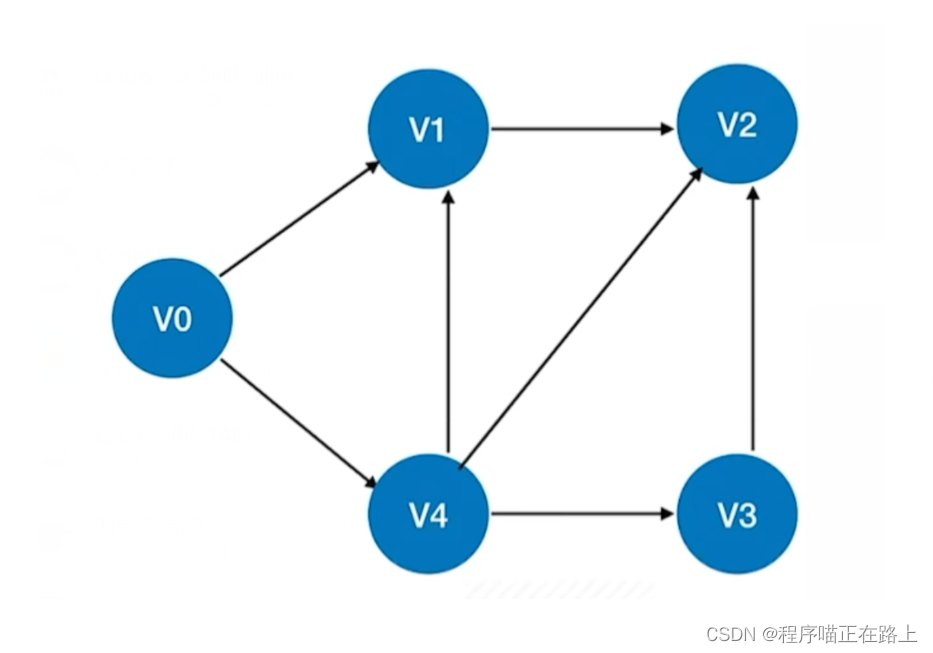
如果一个有向图中不存在环，则称之为有向无环图，简称 $DAG$ 图（$DirectedAcyclicGraph$），比如下面这个图

DAG 描述表达式

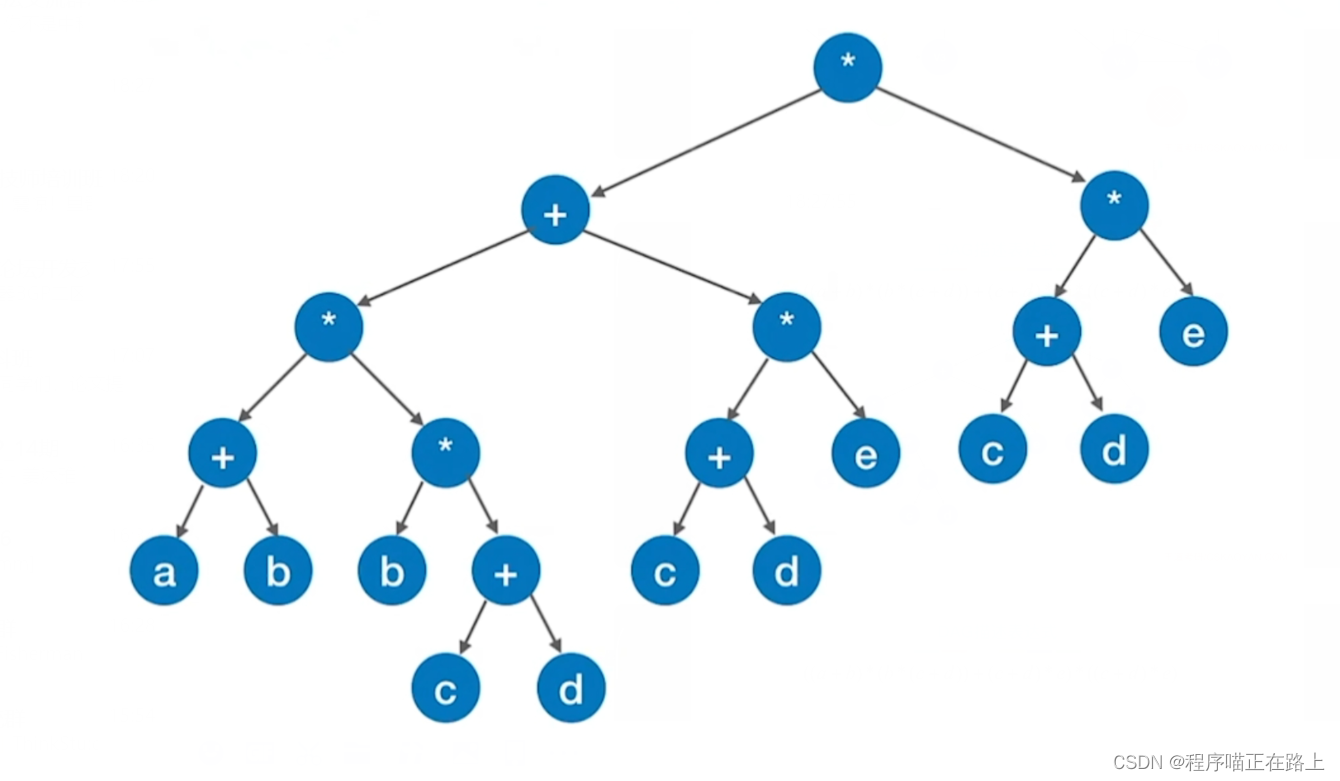
有下面这样一个表达式：

$((a+b)\ast (b\ast (c+d))+(c+d)\ast e)\ast ((c+d)\ast e)$

我们可以将其表示成树的形式：

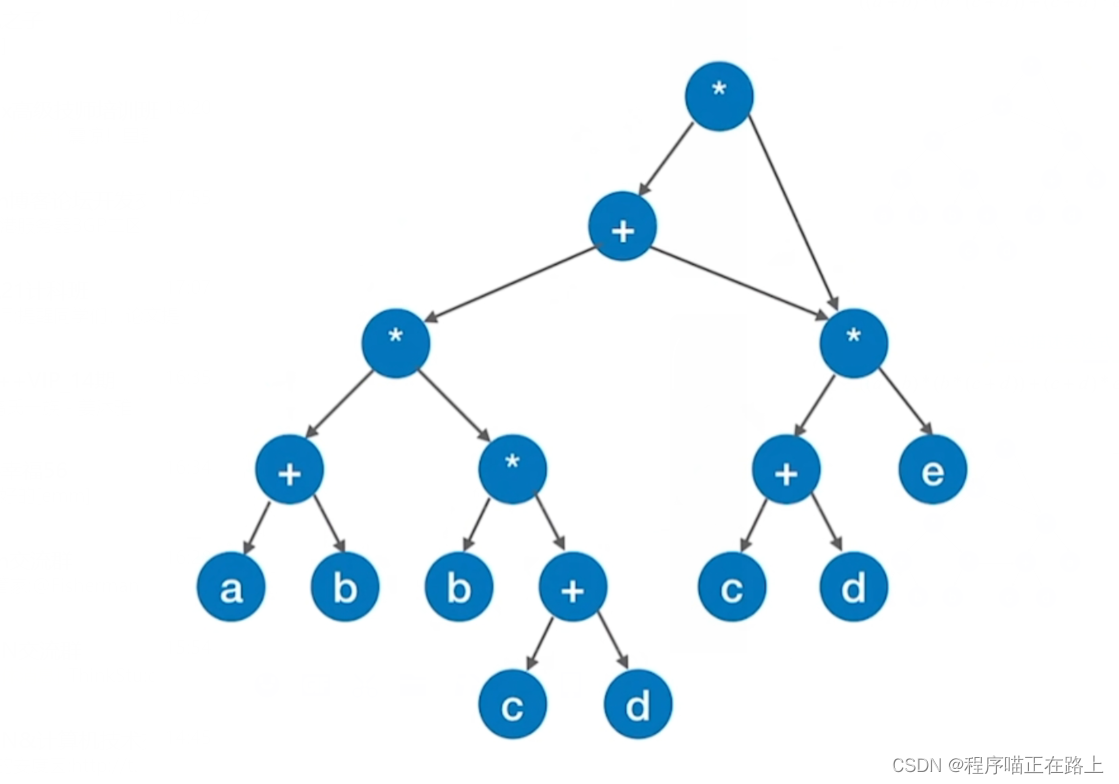
但是我们会发现，树中有些地方是重复的，比如 $(c+d)\ast e$ 这部分，所以我们删除一部分，变成

接着我们发现还有 $c+d$ 这部分也重复了，也得删去

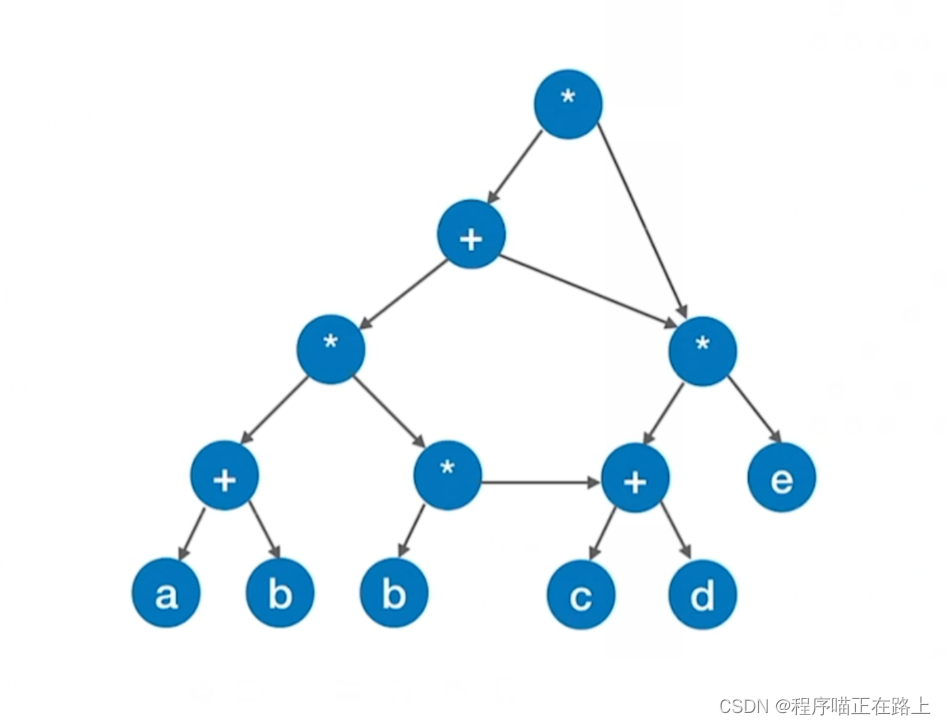
最后还有 $b$ 也重复

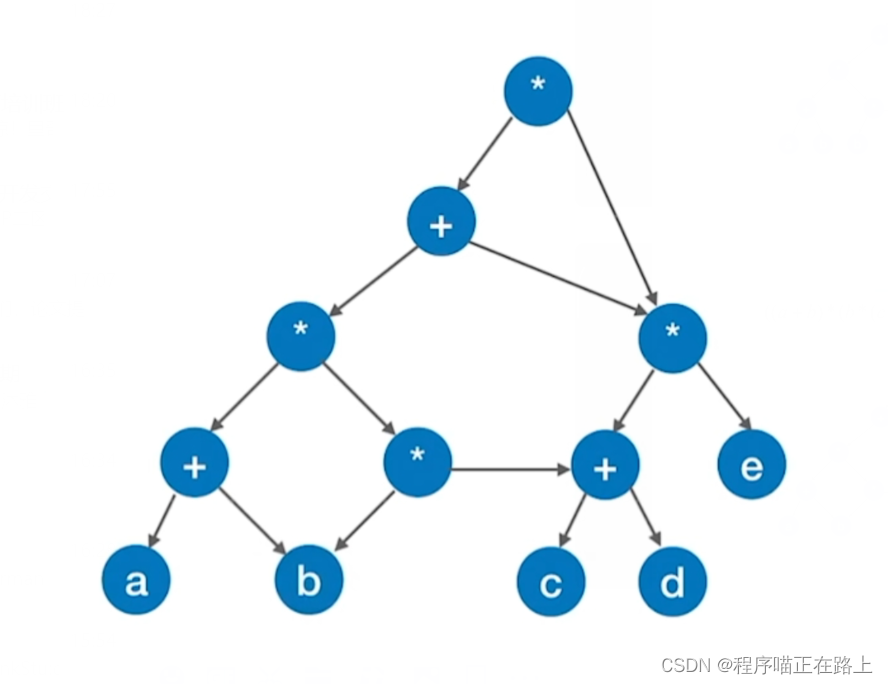
规律：顶点中不可能出现重复的操作数

解题方法

1. 把各个操作数不重复地排成一排
   

2. 标出每个运算符的生效顺序（先后顺序有点出入无所谓）
   

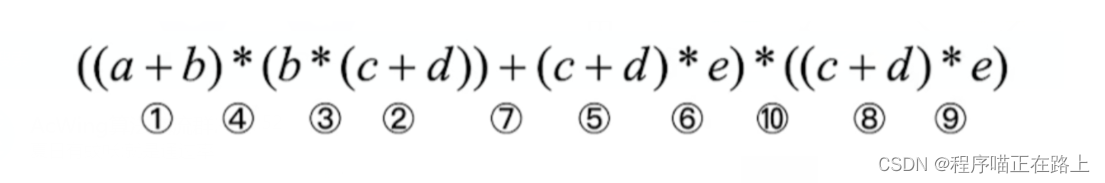
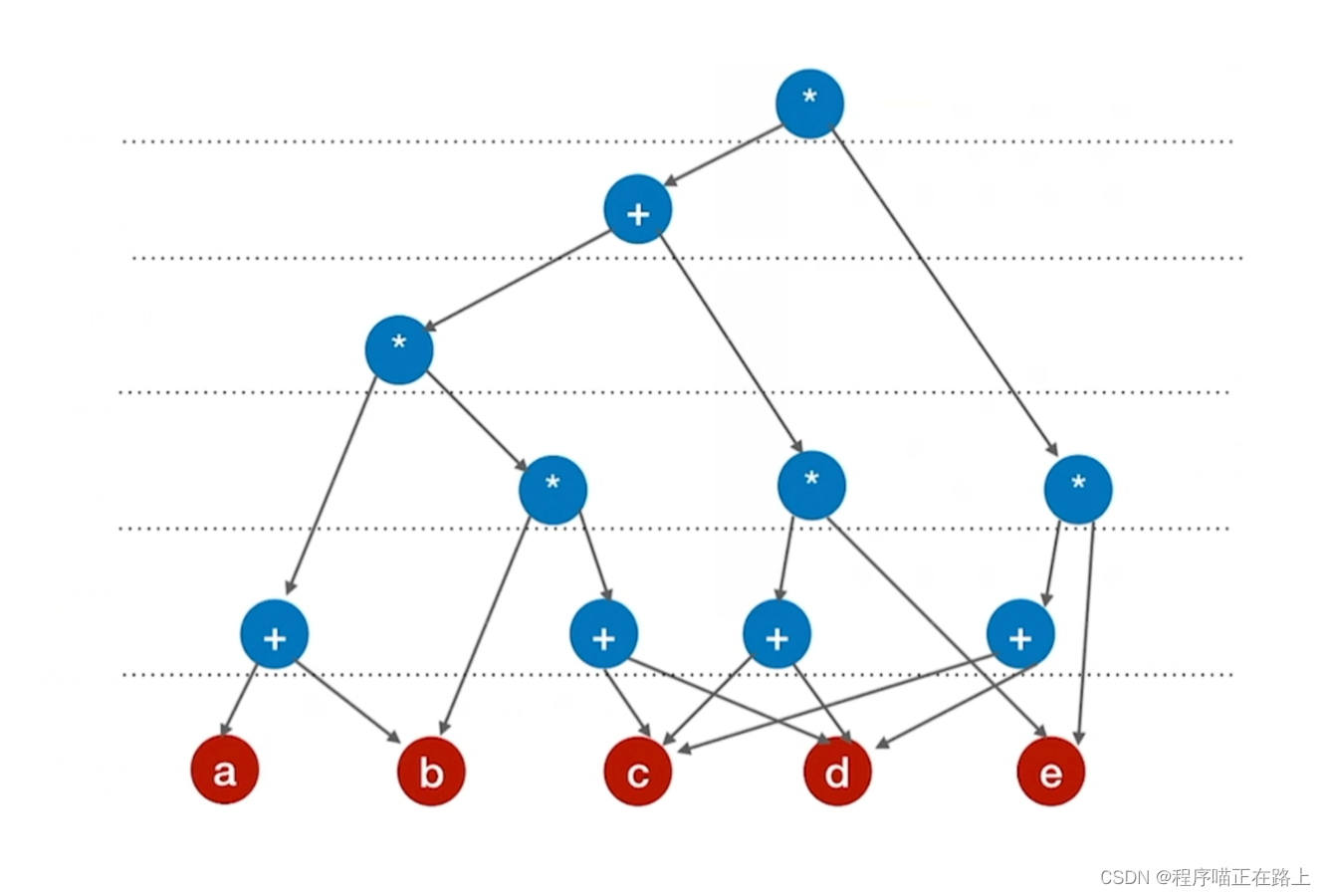
3. 按顺序加入运算符，注意 “分层”
   

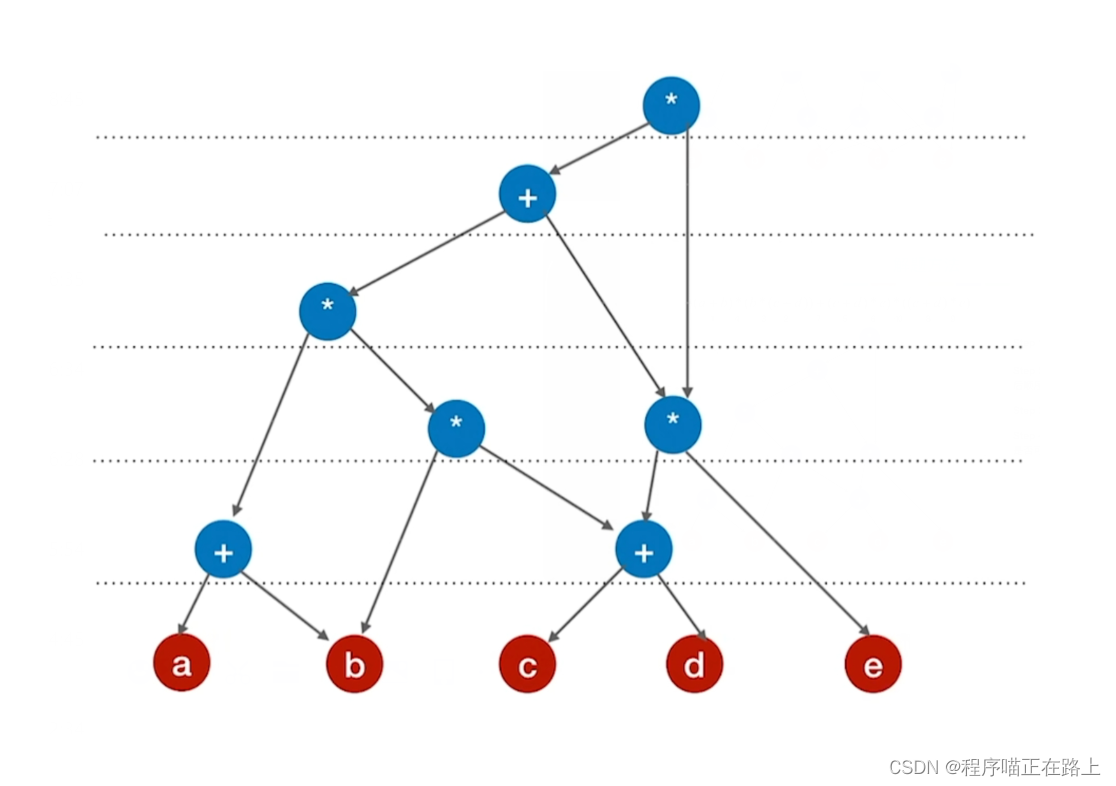
4. 从底向上逐层检查同层的运算符是否可以合体
   

拓扑排序

AOV网

$AOV$ 网（$ActivityOnVertexNetWork$，用顶点表示活动的网）：用 $DAG$ 图（有向无环图）表示一个工程。顶点表示活动，有向边 $<V_i,V_j>$ 表示活动 $V_i$ 必须先于活动 $V_j$ 进行

拓扑排序

在图论中，由一个有向无环图的顶点组成的序列，当且仅当满足下列条件时，称为该图的一个拓扑排序：

• 每个顶点出现且只出现一次
• 若顶点 $A$ 在序列中排在顶点 $B$ 的前面，则在图中不存在从顶点 $B$ 到顶点 $A$ 的路径

每个 $AOV$ 网都有一个或多个拓扑排序序列

拓扑排序的实现：

1. 从 $AOV$ 网中选择一个没有前驱（入度为 $0$）的顶点并输出
2. 从网中删除该顶点和所有以它为起点的有向边
3. 重复 $1$ 和 $2$ 直到当前的 $AOV$ 网为空或者当前网中不存在无前驱的顶点为止

#define MaxVertexNum 100				//图中顶点数目的最大值
typedef struct ArcNode {				//边表结点
	int adjvex;							//该弧所指向的顶点的位置
	struct ArcNode *nextarc;			//指向下一条弧的指针
	//InfoType info;					//网的边权值
}ArcNode;

typedef struct VNode {					//顶点表结点
	VertexType data;					//顶点信息
	ArcNode *firstarc;					//指向第一条依附该顶点的弧的指针
}VNode, AdjList[MaxVertexNum];

typedef struct {
	AdjList vertices;					//邻接表
	int vexnum, arcnum;					//图的顶点数和弧数
}Graph;									//Graph是以邻接表存储的图类型

bool TopologicalSort(Graph G) {
	InitStack(S);				//初始化栈，存储入度为0的顶点
	for (int i = 0; i < G.vexnum; ++i) {
		if (indegree[i] == 0) Push(S, i);		//将所有入度为0的顶点进栈
	}
	int count = 0;				//计数，记录当前已经输出的顶点数
	while (!IsEmpty(S)) {		//栈不空，则存在入度为0的顶点
		Pop(S, i);				//栈顶元素出栈
		print[count++] = i;		//输出顶点i
		
		for (p = G.vertices[i].firstarc; p; p = p->nextarc) {
			//将所有i指向的顶点的入度减1，并且将入度减为0的顶点压入栈S
			v = p->adjvex;
			if (!(--indegree[v])) Push(S, v);	//入度为0，则入栈
		}//for
	}//while

	if (count < G.vexnum) return false;		//排序失败，有向图中有回路
	else return true;						//拓扑排序成功

其中 indegree 是记录各个顶点入度的数组，初始化为各顶点的入度；print 是记录拓扑序列的数组，初始化为 $-1$

在这个拓扑排序中，每个顶点和每条边都需要处理一次，整体的时间复杂度为 $O(|V|+|E|)$，如果是采用邻接矩阵存储的图，则需要 $O(|V{|}^2)$ 的时间复杂度

逆拓扑排序

逆拓扑排序的实现：

1. 从 $AOV$ 网中选择一个没有后继（出度为 $0$）的顶点并输出
2. 从网中删除该顶点和所有以它为终点的有向边
3. 重复 $1$ 和 $2$ 直到当前的 $AOV$ 网为空

逆拓扑排序的实现（DFS算法）

void DFSTraverse(Graph G) {				//对图G进行深度优先遍历
	for (v = 0; v < G.vexnum; ++v) 		//初始化已访问标记数据
		visited[v] = false;
		
	for (v = 0; v < G.vexnum; ++v)
		if (!visited[v]) DFS(G, v);
}

void DFS(Graph G, int v) {				//从顶点v开始，深度优先遍历图G
	visited[v] = true;					//设置已访问标记
	for (w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
		if (！visited[w]) DFS(G, w);
	
	print(v);			//输出顶点
}

如果图中存在回路，那么上面的程序就不再使用，我们需要给每个顶点添加一个是否已经入栈的标记来判断是否有回路即可

关键路径

AOE网

在带权有向图中，以顶点表示事件，以有向边表示活动，以边上的权值表示完成该活动的开销（如完成该活动所需的时间），称之为哟个边表示活动的网络，简称 $AOE$ 网（$ActivityOnEdgeNetWork$）

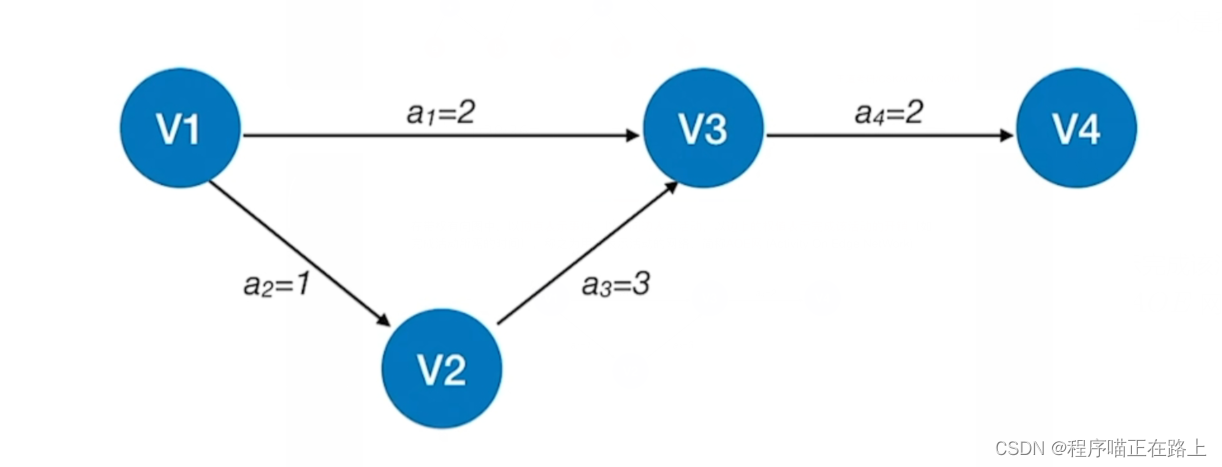
$AOE$ 网具有以下两个性质：

• 只有在某顶点所代表的事件发生后，从该顶点出发的各有向边所代表的活动才能开始
• 只有在进入某顶点的各有向边所代表的活动都已结束时，该顶点所代表的事件才能发生。另外，有些活动是可以并行进行的

在 $AOE$ 网中仅有一个入度为 $0$ 的顶点，称为开始顶点（源点），它表示整个工程的开始；也仅有一个出度为 $0$ 的顶点，称为结束顶点（汇点），它表示整个工程的结束

从源点到汇点的有向路径可能有多条，所有路径中，具有最大路径长度的路径称为关键路径，而把关键路径上的活动称为关键活动

完成整个工程的最短时间就是关键路径的长度，若关键活动不能按时完成，则整个工程的完成时间就会延长

事件 $v_k$ 的最早开始时间 $ve(k)$ —— 决定了所有从 $v_k$ 开始的活动能够开工的最早时间

活动 $a_i$ 的最早开始时间 $e(i)$ —— 指该活动弧的起点所表示的事件的最早发生时间

事件 $v_k$ 的最迟开始时间 $vl(k)$ —— 它是指在不推迟整个工程完成的前提下，该事件最迟应该发生的时间

活动 $a_i$ 的最迟开始时间 $l(i)$ —— 它是指该活动弧的终点所表示事件的最迟发生时间与该活动所需时间之差

活动 $a_i$ 的时间余量 $d(i)=l(i)-e(i)$，表示在不增加完成整个工程所需总时间的情况下，活动 $a_i$ 可以拖延的时间；若一个活动的时间余量为零，则说明该活动必须要如期完成，$d(i)=0$ 即 $l(i)=e(i)$ 的活动是关键活动，由关键活动组成的路径就是关键路径

求关键路径的步骤

1. 求所有事件的最早发生时间 $ve()$
2. 求所有事件的最迟发生时间 $vl()$
3. 求所有活动的最早发生时间 $e()$
4. 求所有活动的最迟发生时间 $l()$
5. 求所有活动的时间余量 $d()$

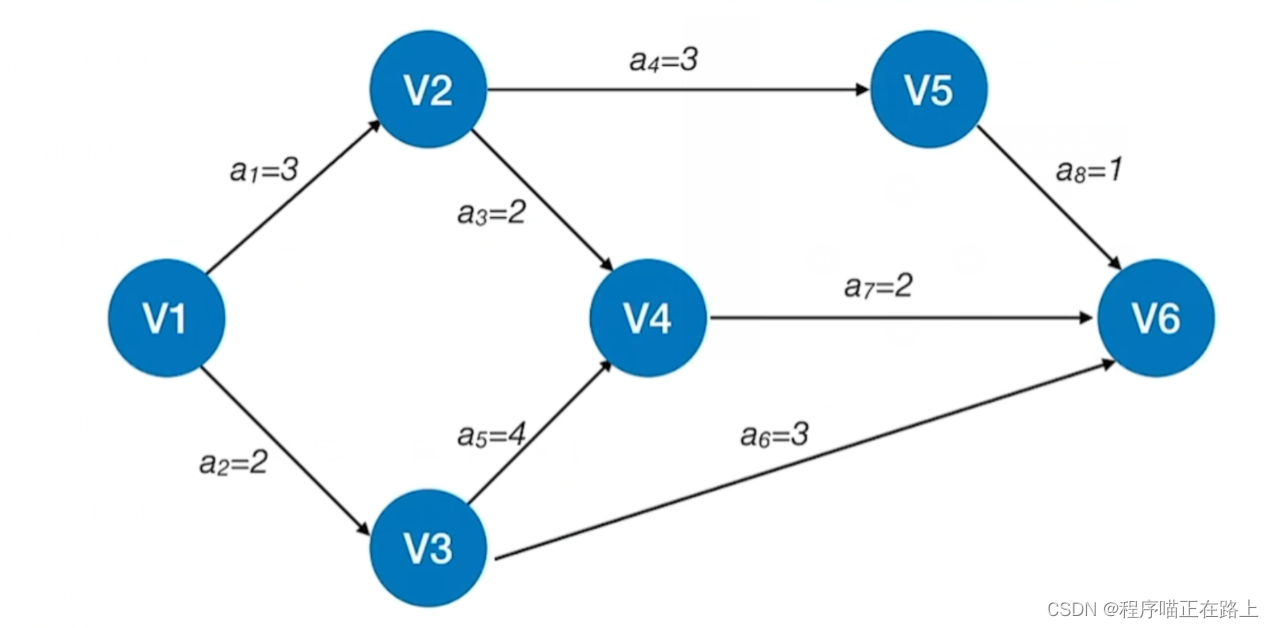
① 求所有事件的最早发生时间 $ve()$

按拓扑排序序列，依次求各个顶点的 $ve(k)$：

• $ve$( 源点 ) $=0$
• v e ( k ) = M a x { v e ( j ) + W e i g h t ( v j , v k ) } ve(k) = Max\{ve(j) + Weight(v_j, v_k)\} ve(k)=Max{ve(j)+Weight(vj​,vk​)}， $v_j$ 为 $v_k$ 的任意前驱

上图的拓扑序列为：$V_1、V_3、V_2、V_5、V_4、V_6$

那么

$ve(1)=0$

$ve(3)=2$

$ve(2)=3$

$ve(5)=6$

v e ( 4 ) = m a x { v e ( 2 ) + 2 , v e ( 3 ) + 4 } = 6 ve(4) = max\{ve(2) + 2, ve(3) + 4\} = 6 ve(4)=max{ve(2)+2,ve(3)+4}=6

v e ( 6 ) = m a x { v e ( 5 ) + 1 , v e ( 4 ) + 2 , v e ( 3 ) + 3 } = 8 ve(6) = max\{ve(5) + 1, ve(4) + 2, ve(3) + 3\} = 8 ve(6)=max{ve(5)+1,ve(4)+2,ve(3)+3}=8

② 求所有事件的最迟发生时间 $vl()$

按逆拓扑排序序列，依次求各个顶点的 $vl(k)$：

• $vl$(汇点) $=$ $ve$(汇点)
• v l ( k ) = M i n { v l ( j ) + W e i g h t ( v k , v j ) } vl(k) = Min\{vl(j) + Weight(v_k, v_j)\} vl(k)=Min{vl(j)+Weight(vk​,vj​)}， $v_j$ 为 $v_k$ 的任意后继

上图的逆拓扑序列为：$V_6、V_5、V_4、V_2、V_3、V_1$

那么

$vl(6)=8$

$vl(5)=7$

$vl(4)=6$

v l ( 2 ) = m i n { v l ( 5 ) − 3 , v l ( 4 ) − 2 } = 4 vl(2) = min\{vl(5) - 3, vl(4) - 2\} = 4 vl(2)=min{vl(5)−3,vl(4)−2}=4

v l ( 3 ) = m i n { v l ( 4 ) − 4 , v l ( 6 ) − 3 } = 2 vl(3) = min\{vl(4) - 4, vl(6) - 3\} = 2 vl(3)=min{vl(4)−4,vl(6)−3}=2

v l ( 1 ) = m i n { v l ( 2 ) − 3 , v l ( 3 ) − 2 } = 0 vl(1) = min\{vl(2) - 3, vl(3) - 2\} = 0 vl(1)=min{vl(2)−3,vl(3)−2}=0

③ 求所有活动的最早发生时间 $e()$

若边 $<v_k,v_j>$ 表示活动 $a_i$，则有 $e(i)=ve(k)$，说白了就等于活动 $a_i$ 所在弧的弧尾的事件的最早发生时间 $ve(k)$，所以

$e(1)=ve(1)=0,e(2)=ve(1)=0,e(3)=ve(2)=3,e(4)=4,e(5)=ve(3)=2,e(6)=2,e(7)=6,e(8)=6$

④ 求所有活动的最迟发生时间 $l()$

若边 $<v_k,v_j>$ 表示活动 $a_i$，则有 $l(i)=vl(j)-Weight(v_k,v_j)$，所以

$l(1)=vl(2)-3=1,l(2)=vl(3)-2=0,l(3)=4,l(4)=4,l(5)=2,l(6)=5,l(7)=6,l(8)=7$

⑤ 求所有活动的时间余量 $d()$

$d(i)=l(i)-e(i)$

方面	$a_1$	$a_2$	$a_3$	$a_4$	$a_5$	$a_6$	$a_7$	$a_8$
$e(k)$	0	0	3	3	2	2	6	6
$l(k)$	1	0	4	4	2	5	6	7
$d(k)$	1	0	1	1	0	3	0	1

关键活动：$a_2、a_5、a_7$

关键路径：$V_1->V_3->V_4->V_6$

关键活动、关键路径的特性

• 若关键活动耗时增加，则整个工程的工期将增长
• 缩短关键活动的时间，可以缩短整个工程的工期
• 当缩短到一定程度时，关键活动可能会变成非关键活动
• 可能有多条关键路径，只提高一条关键路径上的关键活动并不能缩短整个工程的工期，只有加快那些包括在所有关键路径上的关键活动才能达到缩短工期的目的