​

论文解读

郭王懿，孙楚天，陈泰劼，张云天

​ 编者按

共乘出行极大地改变了人们的日常出行方式。如何高效运营背后的双边平台是极具挑战性的工作。滴滴出行、Lyft公司是其中的佼佼者。本专题将探讨双边平台运营中的一个关键问题：如何科学度量双边平台的运营效率？

本专题分为上下两篇，递进推出。其中，上篇围绕滴滴出行、上海财经大学发表在统计学“四大”期刊之一《Journal of the American Statistical Association》的一篇文章 [1] 展开；下篇关注解读Lyft公司的一篇优质技术博客 [2]。

引言

近年来，动态多时空供需网络被应用于气候科学、社会科学、神经科学等多个学科，网约车平台的动态需求和供应网络是多时空动态网络的典型应用。网约车司乘匹配问题是在相同的无向（或有向）图 $G=(\mathbb{V},\mathbb{E})$上匹配“供应”和“需求”两个未归一化的测度序列，其中 $\mathbb{V}$ 和 $\mathbb{E}$ 分别是顶点集和连接顶点组的边集。具体的做法是将一个城市划分为数百个不重叠的网格，作为顶点集 $\mathbb{V}$，边结构 $\mathbb{E}$ 由道路网络和位置功能确定。在每个决策时间段内通过观测订单需求和空闲司机的分布，使用订单分发策略将客户请求与可能的周围空闲司机进行匹配。

本文考虑的基本问题是如何量化描述双边市场动态多时空供需网络的空间匹配程度，特别是网约车平台（例如 Uber 和 DiDi）。在基于转移成本的匹配度定义下，计算出最优匹配度就意味着计算出将供应网络分布转移到需求网络分布的最优转移策略，即订单分配策略，因此研究多时空供需网络的匹配度非常关键。为了解决这个问题，首先引入一个加权图结构$(G,W,C)$来描述城市的交通网络和交通成本。具体来说，将每个市场划分为 N 个不相交的区域，并将它们视为顶点，表示为 V = { v 1 , . . . , v N } \mathbb{V} = \{v_1, . . . , v_N\} V={v1​,...,vN​}。设$\mathbb{E}$是任意可能的顶点对之间的边集，使得$(vi,vj)\in \mathbb{E}\subset \mathbb{V}\times \mathbb{V}$是具有非负权重$w_{ij}$（例如，运输成本）的边。对于所有$w_{ij}$，设$w_{ij}$。加权图结构包括一个无向（或有向）图$G=(\mathbb{V},\mathbb{E})$以及一个权重矩阵$G=(\mathbb{V},\mathbb{E})$，其中$w_{ij}$是非负权重。从$w_{ij}$到$v_j$的基于图的运输成本定义为 c i j = m i n K ≥ 0 , ( i k ) k = 0 K : v i → v j { ∑ k w i k , i k + 1 : ∀ k ∈ [ [ 0 , K − 1 ] ] , ( v i k , v i k + 1 ) ∈ E } c_{ij} = min_{K≥0,(i_k)_{k=0}^{K}:vi→vj} \{\sum_k w_{i_k,i_{k+1}} : ∀k ∈[[0, K - 1]],(v_{i_k}, v_{i_k+1}) ∈ \mathbb{E}\} cij​=minK≥0,(ik​)k=0K​:vi→vj​{∑k​wik​,ik+1​​:∀k∈[[0,K−1]],(vik​​,vik​+1​)∈E}，其中$(i_k{)}_{k=0}^K:v_i\to v_j$代表以$v_{i_0}=v_i$开始并以$v_{i_K}=v_j$结束的$G$上通过$\mathbb{E}$的任何路径。因此，$c_{ij}$是从$v_i$到$v_j$的测地距离，即从$v_i$到$v_j$运输一个单位物体的最小成本。因此，可以在$(G,W)$上定义一个运输成本矩阵，表示为$C=(c_{ij})\in R^{N\times N}$。

其次，需要引入一个距离来量化每个时间区间上的需求和供应质量间的差异，以及在$(G,W,C)$上跨时间的差异。在给定的时间区间上，定义${\nu }_j=\nu (v_j)$和${\mu }_j=\mu (v_j)$为顶点$v_j$的点质量两个Lebesgue测度$\nu$和$\mu$，分别代表了打车平台节点$v_j$内的用户请求和可用司机的数量。每个时间段的供应和需求网络可以建模为$(G,W,C)$上的两个离散的Lebesgue测度$\mu$和$\nu$。

基于最佳传输理论的 Wasserstein 类度量已被证明是度量复杂空间中对象的有效工具。然而，现有的Wasserstein类度量并不直接适用于在2.1节中详细定义的$(G,W,C)$上的两个不均衡度量的比较。因此，作者引入了一种基于图的均衡度量(GEM)，并将其表述为一个不均衡的最优运输问题。

一、基于图结构的均衡度量方法

1. 现有的Wasserstein类距离

有很多经典的度量两个分布之间差异的标准，大致分为两类，第一类是用像素的差异定义距离，第二类是基于转移成本定义的距离。$L_p$距离、TV距离、KL散度等都是第一类度量准则，Hellinger距离是经典案例:
$D_H^2(\mu ,v)=0.5{\int }_X{\left(\sqrt{d\mu /d{\nu }_0}-\sqrt{d\nu /d{\nu }_0}\right)}^{2}d{\nu }_0$,意味衡量两个分布在测度${\nu }_0$上的均方根差异。但这一类基于像素差异的指标有两大主要缺陷：

• Hellinger类指标没有考虑不同位置的连接关系，即没有考虑$X$的拓扑分布。
• Hellinger类指标需要进行归一化操作，即要求$\mu (X)={\int }_{X}d\mu =\nu (X)={\int }_{X}d\nu$。

为了解决如上两个缺陷，部分学者提出了Wasserstein距离等第二类基于转移成本的距离，在组合优化等分配问题领域有很深的研究。Wasserstein距离的定义如下：
D W ( μ , v ∣ c ) = inf ⁡ γ ∈ M + ( X × Y ) { ∫ X × Y c d γ + ι { = } ( P # X γ ∣ μ ) + ι { = } ( P # Y γ ∣ v ) } \begin{aligned} & D_W(\mu, v \mid c) =\inf _{\gamma \in M_{+}(X \times Y)}\left\{\int_{X \times Y} c d \gamma+\iota_{\{=\}}\left(P_{\#}^X \gamma \mid \mu\right)+\iota_{\{=\}}\left(P_{\#}^Y \gamma \mid v\right)\right\} \end{aligned} ​DW​(μ,v∣c)=γ∈M+​(X×Y)inf​{∫X×Y​cdγ+ι{=}​(P#X​γ∣μ)+ι{=}​(P#Y​γ∣v)}​

其中$X,Y$是两个Hausdorff拓扑空间，损失函数c是 X × Y → R ∪ { ∞ } X \times Y \rightarrow R \cup\{\infty\} X×Y→R∪{∞}的映射，转移函数$\gamma$被定义为一个非负测度$\gamma \in M_{+}(X\times Y)$，等式约束 ι { = } ( α ∣ β ) \iota_{\{=\}}(\alpha \mid \beta) ι{=}​(α∣β)代表当$\alpha =\beta$时为0，其余为无穷。该度量的前提条件是$\mu \in M_{+}(X)$和$\nu \in M_{+}(Y)$总量一样，即$\mu (X)=\nu (Y)$。$P_{\#}^X\gamma 和P_{\#}^Y\gamma$分别是$\gamma$的两个边际分布。

该方法可以获得最优的分配方案$\gamma$，但当供需总量不一样时，Wasserstein距离无法获得一个可行解，而在实际中通常存在供需分布总量不一致。因此，部分学者提出了基于散度的不均衡运输问题度量方法。首先是$\varphi -$散度的定义。首先有熵函数$\varphi$，对于$\mu ,v\in M(T),\frac{d\mu }{dv}v+{\mu }^{\perp }$是$\mu$对于$\nu$的勒贝格分解。散度$D_{\varphi }$的定义为

$D_{\varphi }(\mu |\nu ):={\int }_T\phi \left(\frac{d\mu }{dv}\right)dv+{\phi }_{\infty }^{\prime }{\mu }^{\perp }(T)$，因此可以定义广义Wasserstein距离(GWD)：
$\begin{array}{r}{D}_{{\phi }_1,{\phi }_2}(\mu ,\nu \mid c)=\underset{\gamma \in M_{+}(X\times Y)}{\inf }\left\{{\int }_{X\times Y}cd\gamma +{\mathcal{D}}_{{\phi }_1}\left(P_{\#}^X\gamma \mid \mu \right)+{\mathcal{D}}_{{\phi }_2}\left(P_{\#}^Y\gamma \mid v\right)\right\}.\end{array}$

GWD用$\varphi -$散度来量化输运计划与供应测度和需求测度两个不平衡测度$\mu$和$\nu$之间的偏差。但是由于GWD测度是基于熵函数$\varphi$的度量，其求解结果${\gamma }^{\ast }$不具有任何物理意义，因此不能提供可靠的调度方案。除此之外，GWD还有以下两个主要问题：

• 很多实际双边平台中，只有一个测度中的质点允许移动， 另一个测度中是固定的，比如打车平台中只有空闲司机的分布可以调度，客户订单是无法移动的。
• 在供需网络中，运输费用通常是一个分布而不是一个常数，并且顶点到自身的运输成本可能不是零。

2.Graph-based Equilibrum Metrics

针对上述research gap，本文提出Graph-based Equilibrum Metrics(GEM)，首先在权重图问题$(G,W,C)$中，我们将供应和需求定义为两个$M_{+}(\mathbb{V})$的测度$\mu ,\nu$，其中$\mu$的质点可以移动，$\nu$的质点是固定的。${\mathcal{N}}_i$定义节点$v_i$的邻接节点集。其次由于交通单行道等原因，$v_i\in {\mathcal{N}}_j$并不能保证$v_j\in {\mathcal{N}}_i$，因此我们定义GEM为：
$\begin{array}{rl}& {\rho }_{\lambda }(\mu ,v\mid G,C)\\ & =\underset{\tilde{\mu }\in M_{+}(\mathbb{V}),\gamma \in M_{+}(\mathbb{V}\times \mathbb{V})}{\inf }\left\{|v-\tilde{\mu }|+\lambda {\int }_{\mathbb{V}\times \mathbb{V}}cd\gamma \right\}\end{array}$

$\begin{array}{rl}s.t.& |\mu |=|\tilde{\mu }|,\left(P_{\#1}^V\gamma \right)\left(v_i\right)=\sum _{v_j\in {\mathcal{N}}_i}\gamma \left(v_i,v_j\right)={\mu }_i\text{ and }\\ & \left(P_{\#2}^V\gamma \right)\left(v_i\right)=\sum _{v_i\in {\mathcal{N}}_j}\gamma \left(v_j,v_i\right)={\tilde{\mu }}_i,\end{array}$

其中$\lambda$是非负的超参数，约束用于限制$\gamma$将$\mu$转移到$\tilde{\mu }$。GEM本质上是Wasserstein距离和供需差异的$L_1$范数。相比于现有的非均衡最有运输问题解决方法，本文提出的GEM有两大优势：

• 考虑到了实际的拓扑信息，只允许邻接节点之间的运输动作，如图所示。
• 可以通过$\lambda$来均衡供需匹配度和运输成本之间的比例。通常通过data-driven的方法来选择模型的$\lambda$。
  
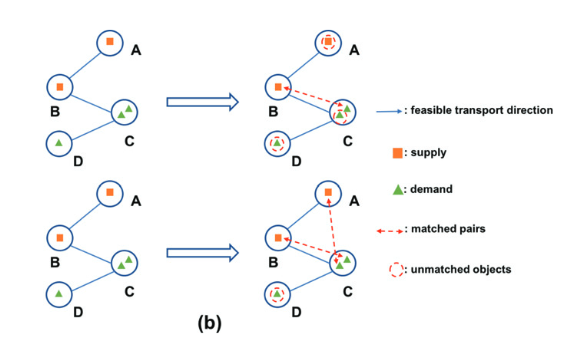
  GEM考虑到拓扑结构，而下图的GWD没有考虑拓扑结构

二、计算方法

GEM的计算方法主要分为两步，第一步是通过紧凑形式对原定义重构，并对绝对值进行线性化处理，第二步是对LP问题进行对偶，降低决策变量的维度。为了描述计算求解过程，我们需要定义一些紧凑形式的变量，首先根据GEM的离散形式定义：
$\begin{array}{rl}& {\rho }_{\lambda }(\mu ,v\mid G,C)=\underset{\gamma \in \Gamma }{\min }\left\{\Vert \mathbf{v}-\tilde{\mathbf{\mu }}{\Vert }_1+\lambda \sum _{v_i\in \mathbb{V}}\sum _{v_j\in \mathbb{V}}{c}_{ij}{\gamma }_{ij}\right\}\\ & \text{ subject to }\sum _{v_j\in {\mathcal{N}}_i}{\gamma }_{ij}={\mu }_i,\sum _{v_j\notin {\mathcal{N}}_i}{\gamma }_{ij}=0,\forall i,\text{ and }\\ & {\tilde{\mu }}_i=\sum _{v_i\in {\mathcal{N}}_j}{\gamma }_{ji}\text{ for }\forall v_i\in \mathbb{V},\end{array}$

对于$v_j\notin {\mathcal{N}}_i$的${\gamma }_{ij}$,其取值一定是0，因此使用 γ ~ = V e c { γ i j , j ∈ N i } ∈ R N 0 × 1 \tilde{\gamma}=Vec\{\gamma_{ij},j\in\mathcal{N}_i\}\in R^{N_0\times1} γ~​=Vec{γij​,j∈Ni​}∈RN0​×1来简化$\gamma$，其中$N_0={\sum }_{i=1}^N{n}_i$代表所有节点的相邻节点总数目之和。这种简化方式可以变量的复杂度从$O(N^2)$降低到$O(N_0)$。为了方便后续计算，现在定义$A_1,A_2$两个$N\times N_0$的矩阵，$A_1$的第${\sum }_{j=1}^{i-1}{n}_j+1$到${\sum }_{j=1}^i{n}_j$的元素全为1，以外的元素全是0；$A_2$则是${\sum }_{p=1}^{j-1}{n}_p+1$到${\sum }_{p=1}^j{n}_p$之间是1，其余是0。$A_1$结构示意图如下所示，

如果所有的路径是双向联通的，即问题是一个无向图即${\gamma }_{ij}={\gamma }_{ji}$，则$A_1$与$A_2$完全一样。因为这里$A_1$与$A_2$分别代表$P_{\#1}^V\gamma$和$P_{\#2}^V\gamma$。

我们定义$\tilde{C}\in R^{N_0\times 1}$是成本向量，用于描述每个路径的单位运输成本。因此我们定义:

$$\begin{gathered} A=\left[\begin{array}{llllllllll}{A}_1& 0& 0& 0\Vert A_2& {\mathbf{I}}_N& -{\mathbf{I}}_N& 0\Vert A_2& -{\mathbf{I}}_N& 0& {\mathbf{I}}_N\end{array}\right], \\ \mathbf{b}={\left[{\mathbf{\mu }}^T,{\mathbf{v}}^T,{\mathbf{v}}^T\right]}^T, \end{gathered}$$

其中，$\mathbf{\mu }={\left({\mu }_1,\dots ,{\mu }_N\right)}^T,A\in R^{3N\times \left(N_0+3N\right)},\mathbf{b}\in R^{3N}$,${\mathrm{I}}_N$是单位阵。

将上述紧凑形式的变量引入定义式可以重构为：
$$\begin{gathered} \min \left\{{\Vert \mathbf{v}-A_2\tilde{\gamma }\Vert }_1+\lambda {\tilde{C}}^T\tilde{\gamma }\right\} \\ \text{subject to}{A}_1\tilde{\gamma }=\mu ,\tilde{\gamma }\ge 0. \end{gathered}$$

引入$S\in R^{N\times 1}$将非线性项线性化以后等价于:

$\begin{array}{rl}& \min \left\{1^{T}S+\lambda {\tilde{C}}^T\tilde{\gamma }\right\}\\ & \text{ subject to }{A}_1\tilde{\gamma }=\mathbf{\mu },A_2\tilde{\gamma }+S\ge \mathbf{v},A_2\tilde{\gamma }-S\le \mathbf{v},\tilde{\gamma }\ge 0,\text{ and }S\ge 0,\end{array}$

上述线性规划问题可以写为紧凑形式：
$\begin{array}{rl}& \underset{X}{\min }\left\{B^{T}X\right\}\\ & \text{ subject to }AX=\mathbf{b},X\ge 0,\end{array}$

其中$B={\left(\lambda {\tilde{C}}^T,1^T,0^T,0^T\right)}^T$,$ X=\left(\tilde{\gamma}^T, S^T, \boldsymbol{w}_1^T, \boldsymbol{w}_2^T\right)T,$${\mathbf{w}}_1^T,{\mathbf{w}}_2^T$是不等式约束转为等式约束的松弛变量，将其矩阵拆解可以表示为下图。

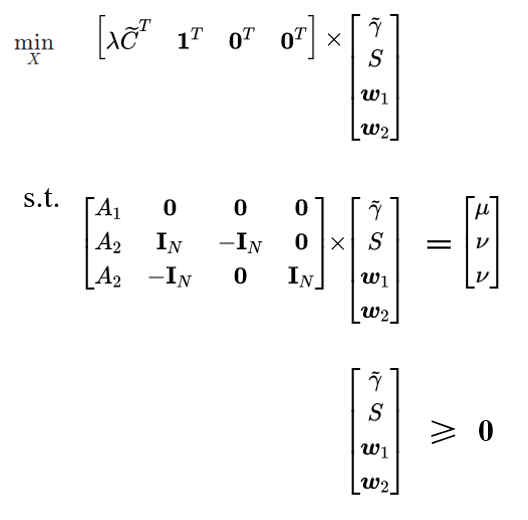
该典型LP问题的对偶形式为

$\begin{array}{rl}& \underset{\mathbf{y}\in R^{3N}}{\max }\left\{{\mathbf{b}}^T\mathbf{y}\right\}\\ & \text{ subject to }{A}^T\mathbf{y}\le B\end{array}$

按照矩阵拆解的示意图如下所示：

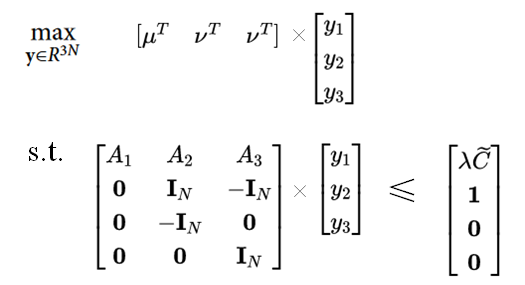
对偶之后的LP问题的变量维度可以从$N_0+3N$缩减到$3N$.

三、GEM在共乘出行平台的三方面应用

首先需要基于每个城市的环境建立动态权重的图结构，首先将城市分为不重合的$N$个正六边形，${\mathcal{N}}_i={\cup }_{k=0}^2{\mathcal{N}}_i^k$其中${\mathcal{N}}_i^k$是${\nu }_i$的第$k$层外部节点，第零层只有它本身。构建$G=(\mathbb{V},\mathbb{E})$,下一步构建$W_t=(w_{ijt})$，其中$w_{ijt}$是两个顶点在$t$时间段的距离，下一步通过$W_t$计算$C_t=(c_{ijt})$。最后得到动态权重图$(G,W_t,C_t)$

1. 应答率预测

指标定义

首先可以测量观测到的动态供应网络与需求网络之间的实时最优距离，定义$\mathbf{O}=\{(o_{it}){\}}_t$,$\mathbf{D}=\{(d_{it}){\}}_t$分别为需求和供应动态系统。定义${\mu }_t=(d_{it}{)}_i,{\nu }_t=(o_{it}{)}_i$,其中i是节点${\nu }_i$的索引。然后求解$\rho (t)={\rho }_{\lambda }\left({\mu }_t,v_t\mid G,C_t\right)$求得t时段的最优运输策略$\left({\tilde{\mu }}_{t\ast }={\left({\tilde{d}}_{it\ast }\right)}_i,{\gamma }_{t\ast }\right)$。

本文将每个顶点${\nu }_i$的最优供需比定义为需求$o_{it}$比上“最优供应” d ~ i t ∗ + ι { = } ( d ~ i t ∗ = 0 ) \tilde{d}_{i t *}+\iota_{\{=\}}\left(\tilde{d}_{i t *}=0\right) d~it∗​+ι{=}​(d~it∗​=0)，记作${\mathrm{DSr}}_{it}$，定义中的第二项为了防止分母为0。同时我们可以定义每个顶点在每个时刻的最优的供需差为${\mathrm{DSd}}_{it}=o_{it}-{\tilde{d}}_{it\ast }$。

在上述两个定义下，我们可以基于GEM测量方法$({\mathrm{DSr}}_{it},{\mathrm{DSd}}_{it})$创造时空地图。进一步的，我们将$({\mathrm{DSr}}_{it},{\mathrm{DSd}}_{it})$扩展到更宽的时间尺度${\mathcal{T}}_0$和一个更大的区域${\mathbb{V}}_0\in \mathbb{V}$，因此本文定义了一个加权平均供需比和一个加权平均供需差：

$\begin{array}{rl}{\mathrm{DSr}}_{{\mathcal{T}}_0}\left({\mathbb{V}}_0\right)& =\frac{{\int }_{t\in {\mathcal{T}}_0}{\sum }_{i\in {\mathbb{V}}_0}{w}_{it}{\mathrm{DSr}}_{it}dt}{{\int }_{t\in {\mathcal{T}}_0}{\sum }_{i\in {\mathbb{V}}_0}{w}_{it}dt}\text{ and }\\ {\mathrm{ADSd}}_{{\mathcal{T}}_0}\left({\mathbb{V}}_0\right)& =\frac{{\int }_{t\in {\mathcal{T}}_0}{\sum }_{i\in {\mathbb{V}}_0}{w}_{it}\left|{\mathrm{DSd}}_{it}\right|dt}{{\int }_{t\in {\mathcal{T}}_0}{\sum }_{i\in {\mathbb{V}}_0}{w}_{it}dt}\end{array}$

这种定义方式中的$w_{it}$可以设置为$o_{it}$来强调高需求节点的指标。一个良好的网约车市场均衡对应着较小的$({\mathrm{DSr}}_{it},{\mathrm{DSd}}_{it})$

算例分析

本文使用DiDi GAIA实验室的2018年四月21日到5月20日的需求数据和空闲的司机数据。将城市分割为了$N=800$个六边形子区域，每个区域边长1400m，设置边权重$w_{ij}$为两个子区域之间的行车距离，并且计算每分钟每个区域内的空闲司机数量和订单数量。

订单应答率通常定义为应答的订单数量除以总的订单数量。本文根据历史数据预测未来10分钟和60分钟的应答率对数值。首先分别计算10分钟间隔的Hellinger距离、L2距离、Wasserstein距离和GEM。其中L2距离和Hellinger距离通过10个连续的一分钟时间间隔的距离计算；Wasserstein距离的计算首先需要将10个连续的一分钟间隔的供需数据进行归一化，来保证可以求得可行的Wasserstein距离。然后我们通过对应的权重，获得每10分钟一个的聚合后的Wasserstein距离度量值。关于GEM相关指标，首先计算每一分钟的${\mathrm{DSr}}_{it}$，然后每十分钟计算一次权重聚合后的${\mathrm{DSr}}_{\mathcal{T}}(V)$。

本文使用百分比绝对值误差(MAPE)和均方根误差(RMSE)来衡量相应指标对预测精度的影响。本文将数据集分为了训练集和测试集，使用线性回归方法，使用先前10个时段的指标和五天前同一时间窗口的历史指标来预测未来6个时刻的订单响应率的对数值。$t+10,t+60$分别代表短时间和长时间尺度的预测，结果如下图所示，可以看出GEM明显优于其他三个指标，传统的指标可能无法充分描述加权图的动态传输和系统平衡。

使用不同指标的应答率预测结果

2. 订单调度策略

通过利用历史数据中的供需两侧信息 { ( D S r i t , D S d i t ) : ( v i , t ) ∈ V × T 0 } \left\{\left(\mathrm{DSr}_{i t}, \mathrm{DSd}_{i t}\right):\left(v_i, t\right) \in \mathbb{V} \times \mathcal{T}_0\right\} {(DSrit​,DSdit​):(vi​,t)∈V×T0​}，我们可以设计大范围的双边平台调度策略。传统的调度策略关注当前时刻需求的满足，比如就近原则以及first-come-first-go策略等，但大多无法利用城市的空间结构，因此无法获得最优的调度。本文利用GEM记录更多的历史供需网络信息，用于描述其对当前订单平均预期收益的影响。$N_o,N_d$分别代表订单数量和空闲司机数量，当吧司机$l$分配给订单$k
$时，$A(k,l)$作为二分图权重是司机的期望收益。$x_{kl}$为1代表订单的分配。因此全局订单分配策略可以归纳为如下二分图匹配问题：
$\begin{array}{rl}& \arg \underset{x_{kl}}{\max }\sum _{k=0}^{N_d}\sum _{l=0}^{N_o}A(k,l)x_{kl},\text{ s.t. }\sum _{k=0}^{N_d}{x}_{kl}\le 1\forall l;\\ & \sum _{l=0}^{N_o}{x}_{kl}\le 1\forall k;x_{kl}=0\text{ if }{c}_{kl}>ϵ\forall k,l.\end{array}$

约束用于保证每个订单最多分配给一个司机，同样每个司机只能接到一个订单。在实际距离中距离如果过远则司机无法接单。

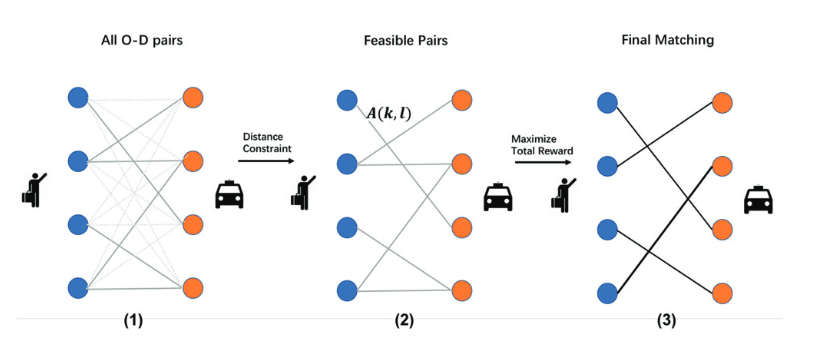
订单分配的二分图匹配问题

本文主要对比基于不同$A(k,l)$的三种调度策略。第一种是只考虑当前分配回报$A^{(1)}(k,l)={\alpha }_1{r}_k-{\alpha }_2{c}_{kl},$这两项分别是收益和距离cost。第二种策略是 A ( 2 ) ( k , l ) = α 1 r k − α 2 c k l + α 3 { η Δ t l k V 1 ( s l k ′ ) − V 1 ( s l ) } , A^{(2)}(k, l)=\alpha_1 r_k-\alpha_2 c_{k l}+\alpha_3\{\eta^{\Delta t_{lk}}V_1(s'_{lk})-V_1(s_{l})\}, A(2)(k,l)=α1​rk​−α2​ckl​+α3​{ηΔtlk​V1​(slk′​)−V1​(sl​)},增加的第三项用于考虑当前动作对未来收益的影响，其中$V_1(s)$是从当前时刻开始到当天结束的期望收益。第三种策略是 A ( 3 ) ( k , l ) = A ( 2 ) ( k , l ) + α 4 { η Δ t l k V 2 ( s l k ′ ) − V 2 ( s l ) } , A^{(3)}(k, l)=A^{(2)}(k, l)+\alpha_4\{\eta^{\Delta t_{lk}}V_2(s'_{lk})-V_2(s_{l})\}, A(3)(k,l)=A(2)(k,l)+α4​{ηΔtlk​V2​(slk′​)−V2​(sl​)},新增的一项用于衡量供需匹配程度，其中$V_2(s)={\nu }_t(v)-{\tilde{\mu }}_t(v)$是通过GEM定义中计算的,$V_2(.)$项可以大大提高顾客被临近司机响应的概率。算例测试如下图所示，结果表明，基于GEM的第三种策略可以获得更高的司机收益和应答率。

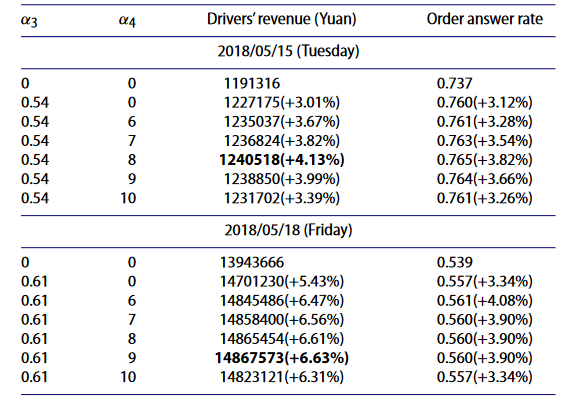
不同调度策略对比

3. 策略评估

本文提出的GEM指标的一个重要应用是直接比较两个（或多个）乘车平台的调度策略。其关键思想是检测在同一平台环境下，两套竞争性策略的GEM之间是否存在显著差异。考虑到平台中需求和供应的联合分布，GEM越小，许多全局运营指标，如订单应答率、订单完成率和司机的工作时间就越好。与这些全局性的运营指标相比，GEM更直接地衡量了一个乘车平台的运营效率。

本文使用2018年12月3日至12月16日同一城市H的另一个供需数据集进行实验，以比较两种订单调度策略之间的有效性。两种策略在连续的半小时的时间间隔内交替执行。此外，本实验从前半小时的基线政策开始，每半小时改变一次政策，贯穿整个一天，并在另一天颠倒它们的顺序。本实验还包括一个A/A测试，通过使用从11月12日到11月25日获得的历史数据作为直接比较，将基线政策与自身进行比较。

每个30分钟的时间窗口内计算GEM的方法如下。每天总共有$M_T=48$个时间区间。为了得到每个时间间隔$\tau$的GEM，本文通过使用归一化权重$o_{it}/{\sum }_{t\in \tau }{\sum }_{v_i\in V}{o}_{it}$汇总了30个GEM值，每个GEM值都是在1分钟的时间戳内计算的。

本文用$y_m(t_k)$表示汇总的GEM值，用$x_m(t_k)$表示2×1的预测因子向量，包括第m日的第k个时间间隔内所有司机的需求总数和总供应时间。$a_m(t_k)=1$代表使用新策略，否则为$-1$。为了考察策略对GEM的边际影响，本文考虑以下回归模型：
y m ( t k ) = β 0 ( t k ) + β 1 ( t k ) T { x m ( t k ) − x ˉ ( t k ) } + β 2 ( t k ) a m ( t k ) + η m ( t k ) + ε m ( t k ) y_m(t_k) = β_0(t_k) + β_1(t_k)^T \{x_m(t_k) − \bar{x}(t_k)\} + β_2(t_k)a_m(t_k) + η_m(_tk) + ε_m(t_k) ym​(tk​)=β0​(tk​)+β1​(tk​)T{xm​(tk​)−xˉ(tk​)}+β2​(tk​)am​(tk​)+ηm​(t​k)+εm​(tk​)

其中，$\beta (t_k)=({\beta }_0(t_k),{\beta }_1(t_k{)}^T,{\beta }_2(t_k){)}^T$是$t_k$处的回归系数向量，$\bar{x}(t_k)$是$k=1,...,M_T$ 的所有$x_i(t_k)$的样本平均值。此外，本文假设${\eta }_m=({\eta }_m(t_1),...,{\eta }_m(t_{M_T}){)}^T$ 和 ${\epsilon }_m=({\epsilon }_m(t_1),...,{\epsilon }_m(t_{M_T}){)}^T$是$M_T\times 1$的随机误差向量，遵循相互独立的多元高斯分布$N(0,{\Sigma }_{\eta })$和$N(0,{\sigma }_{\epsilon }^2\cdot I_{M_T})$，其中${\Sigma }_{\eta }$是一个$M_T\times M_T$矩阵，${\sigma }_{\epsilon }^2$是一个正标度。本文将检验以下的无效假设和备择假设：
$$H_0:{\int }_0^{M_T}{\beta }_2(t)dt=0v.s.H1:{\int }_0^{M_T}{\beta }_2(t)dt\ne 0$$

其中，${\int }_0^{M_T}{\beta }_2(t)dt\approx {\sum }_{k=1}^{M_T}{\beta }_2(t_k)\Delta t_0$表示每天的平均处理效应，其中$\Delta t_0$是每个时间间隔的长度。本文提出了一个基于广义估计方程（GEE）的联合估计程序，迭代估计所有的未知参数，直到达到一个特定的收敛标准。随后，本文计算与每天的平均处理效应相关的$t$检验统计量及其相应的单侧（或双侧）$p$值。

此外，本文在上述回归模型中考虑了三个全局运营指标，包括订单应答率、订单完成率和商品总值（GMV）作为$y_m(t_k)$。本文拟合相应的三个回归模型，以研究新的调度策略是否在运营层面显著改善了骑行平台。

下表总结了A/A和A/B两种实验设计的所有回归分析结果。可以看到，在A/B实验设计中，当用新策略取代旧策略时，平均应答率、完成率和商品总值都存在明显的增加，因为所有与平均处理效应有关的$p$值都小于$10^{-3}$。新策略也可以显著降低GEM值（$p$值小于0.05），这与我们的假设一致，即GEM可以充分量化供需关系，并随后影响所考察的平台指标。相反，在A/A实验设计中，所有四个指标在5%的显著性水平上没有显示出明显的处理效果。

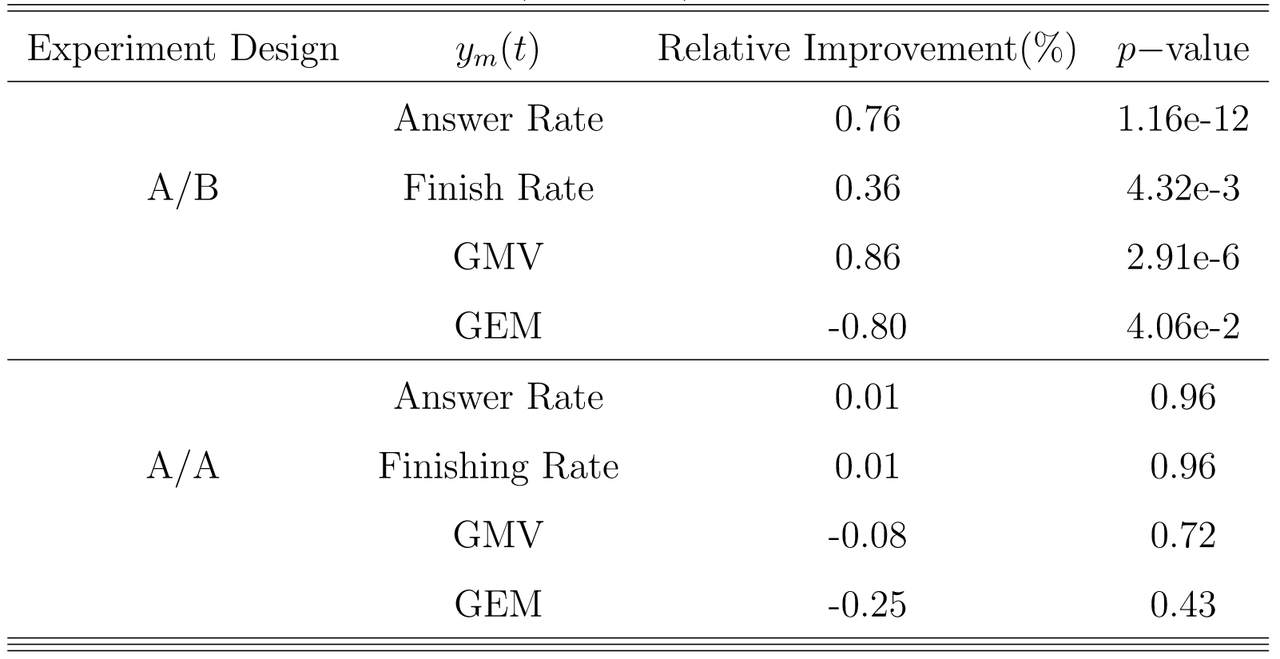
A/A和A/B实验的相对改进百分比和平均处理效应的双侧p值

下图(A)显示了2018年12月3日A/B实验设计中总共48个30分钟时间窗口的GEM值。在早上7:00到8:00的时间段内，策略从控制组改为实验组策时，GEM值明显减少。下图(B)分别显示了调度策略在控制组和实验组下同一时间段内的$DS{d}_{it}$的热图。由绿色和紫色圆圈标记的三个选定区域的客户要求被附近区域的司机满足，导致更高的供需一致性，从而使GEM值更小。

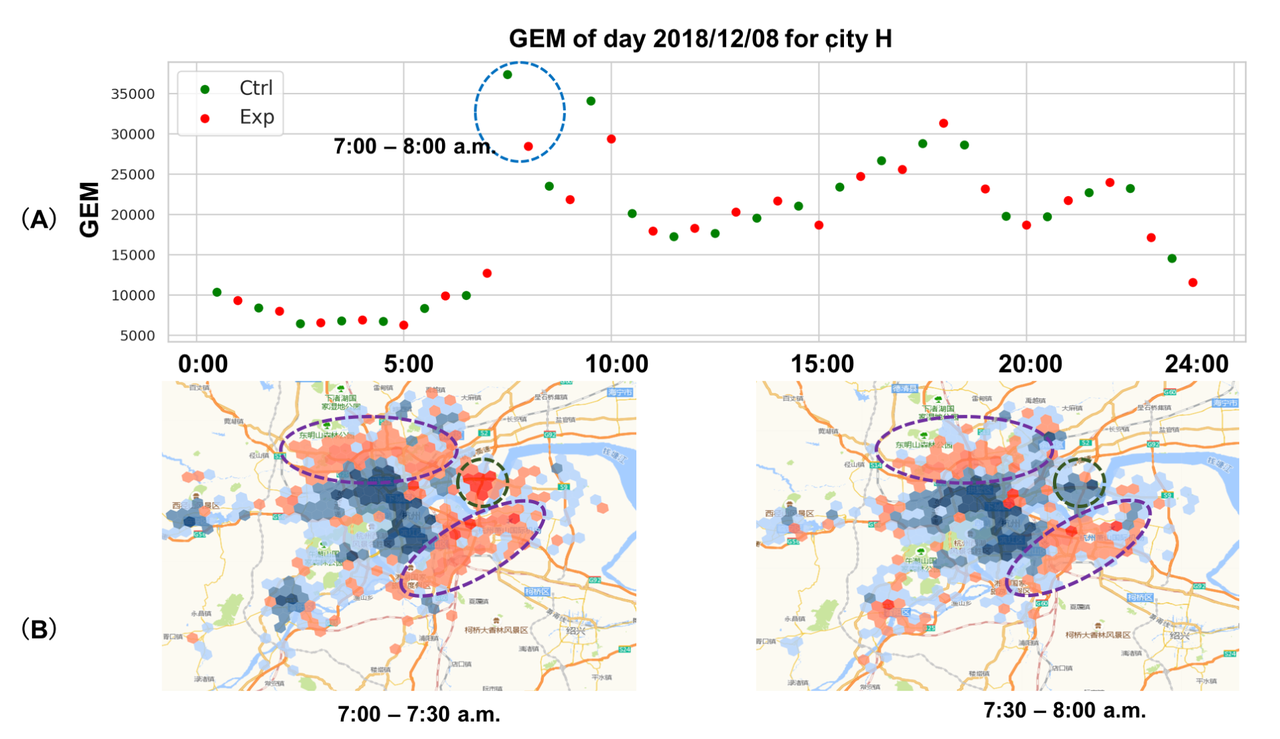
（A）H市在30分钟范围内随机选择的一天(2018/12/08)的GEM值 （B）H市的30分钟范围内控制组(7:00 - 7:30)和实验组(7:30 - 8:00)的供需差热力图

四、小结

总的来说，针对动态供需网络均衡度评估以及网约车双边平台的司乘匹配等问题，本文主要贡献总结如下：

1. 提出了基于图结构的动态供需网络均衡度量方法(GEM)，可以看作是一种受限的广义Wasserstein距离，来量化动态需求和供应网络在加权图结构上的距离。相比于传统方法，GEM不仅考虑了图的拓扑结构，而且考虑了不均衡的供需总量。
2. 通过改变每个节点的物理区域大小，可以得到多级GEM及其对应的最优调度策略。在最精细的空间尺度上，GEM可以计算包含许多局部细节的供需分配调度策略。相比之下，在相对粗糙的空间尺度上，它给出了最优传输函数的低频模式粗略表示。
3. 在数值计算方法上，GEM的计算可以重构为一个标准的线性规划(LP)问题。作者从理论上研究了GEM的几个理论性质，包括计算GEM的LP算法的收敛性、GEM的期望等。并通过LP对偶大大降低了决策变量的复杂度。
4. 在滴滴出行的数据集上应用GEM解决了应答率预测、订单派送策略制定等问题，并达到了很好的效果。

参考文献

[1] Zhou, F., Luo, S., Qie, X., Ye, J., & Zhu, H. (2021). Graph-based equilibrium metrics for dynamic supply–demand systems with applications to ride-sourcing platforms. Journal of the American Statistical Association, 116(536), 1688-1699.
[2] Alex Chin, & Tony Qin. (2023.02.25). Quantifying Efficiency in Ridesharing Marketplaces. Link: https://eng.lyft.com/quantifying-efficiency-in-ridesharing-marketplaces-affd53043db2