Logistic Regression

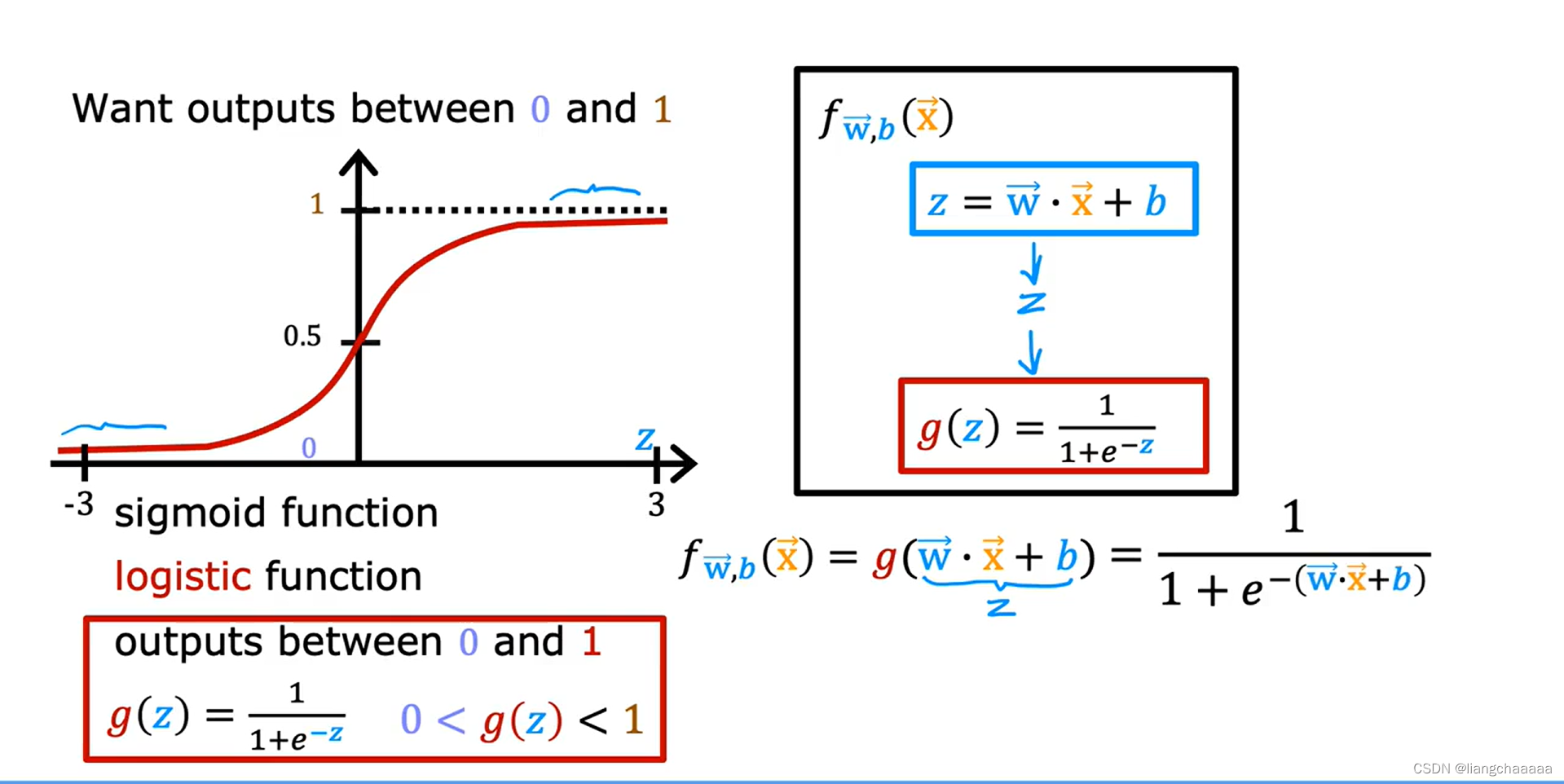
一个用于分类的算法，模型拟合后，以某些值作为阈值，将数据区分为不同的类别。过去的回归算法中，y的值可以范围很广，而在分类算法中y代表类别，往往只有几个，甚至只有两个(true or false)

 

 

凸函数

凸函数的割线在函数曲线的上方。凸优化问题的局部最优解是全局最优解，在数据科学的模型求解中，如果优化的目标函数是凸函数，则局部极小值就是全局最小值。这也意味着我们求得的模型是全局最优的，不会陷入到局部最优值。

代价函数的选择

在逻辑回归算法中，方差作为代价函数来训练数据已经不合适了，因为方差作为代价函数时，代价函数曲线图不是凸函数，会有许多“坑”，梯度下降的时候很容易陷入局部最小值无法跳出。

逻辑回归算法一般采用以下代价函数，这个特殊的成本函数是从统计学中推导出来的，叫极大似然估计

 

y = 1时，f的值越接近1，和y相差的越小，预测的也就越准，同时，代价函数L就越小，即惩罚越小；

y = 0时，f的值越接近0，和y相差的越小，预测的也就越准，同时，代价函数L就越小，即惩罚越小； 

 

 可以看出cost函数修改后图像很平滑，明显有一个全局最优解

代价函数实现

Numpy中有个函数叫exp()，可以输入z,计算出e^(z)的结果

def sigmoid(z):
    z = np.clip(z,-500,500) #防止溢出
    result = 1.0/(1.0+np.exp(-z))
    return result

def compute_cost_logistic(X, y, w, b):
    m = X.shape[0]
    cost = 0.0
    for i in range(m):
        z = np.dot(X[i],w)+b
        f_wb = sigmoid(z)
        cost += -y[i]*np.log(f_wb) - (1-y[i])*np.log(1-f_wb) #同时考虑y的两种情况
        cost /= m
    return cost

 偏导计算

def compute_gradient_logistic(X, y, w, b): 
    m,n = X.shape 
    dj_dw = np.zeros((n,))
    dj_db = 0.0

    for i in range(m):
        z = np.dot(X[i],w)
        f_wb = sigmoid(z)+b
        err = f_wb - y[i]
        for j in range(n):
            dj_dw[j]+= err*X[i,j]
        dj_db += err
    dj_dw /= m
    dj_db /= m
    return dj_dw,dj_db

梯度下降实现

def gradient_descent(X, y, w_in, b_in, alpha, num_iters): 
    J_history = []
    w = copy.deepcopy(w_in)
    b = b_in

    for i in range(num_iters):
        dj_dw,dj_db = compute_gradient_logistic(X,y,w,b)
        w -= alpha*dj_dw
        b -= alpha*dj_db

        if i <100000:
            J_history.append(compute_cost_logistic(X,y,w,b))
    return  w,b,J_history

误差和过拟合

在训练集上的误差称为训练误差（training error）或经验误差（empirical error）。

在测试集上的误差称为测试误差（test error）。

学习器在所有新样本上的误差称为泛化误差（generalization error）。

显然，我们希望得到的是在新样本上表现得很好的学习器，即泛化误差小的学习器。因此，我们应该让学习器 尽可能地从训练集中学出普适性的“一般特征”，这样在遇到新样本时才能做出正确的判别。然而，当学习器把 训练集学得“太好”的时候，即把一些训练样本的自身特点当做了普遍特征；同时也有学习能力不足的情况，即训练集的基本特征都没有学习出来

学习能力过强，以至于把训练样本所包含的不太一般的特性都学到了，称为：过拟合（overfitting）。

学习能太差，训练样本的一般性质尚未学好，称为：欠拟合（underfitting）。  

在过拟合问题中，训练误差十分小，但测试误差教大；在欠拟合问题中，训练误差和测试误差都比较大。目前，欠拟合问题比较容易克服，例如增加迭代次数等，但过拟合问题还没有十分好的解决方案，过拟合是机器学习面临的关键障碍。

正则化解决过拟合问题

结果模型过拟合问题思路：

1.搜集更多数据

2.舍弃某些特征值

3.用正则化的方法缩小参数的大小

正则化通过向损失函数添加一个正则项来约束模型参数的大小。实际上，这些参数（）的值越小，通常对应于越光滑的函数，也就是更加简单的函数。因此就不易发生过拟合的问题,这个额外的项是正则化项系数和进入模型复杂度计算的一部分。lambda使wj不会过大（因为如果lambda*wj很大的话，代价函数会很大，训练的过程中惩罚就比较“狠”），可以有效约束模型的过拟合问题，同时,lambda要做的就是控制在两个不同的目标(模型不会过拟合与梯度下降找最优解)中的平衡关系。

正则化之后梯度下降的改变

正则化后偏导该怎么求？

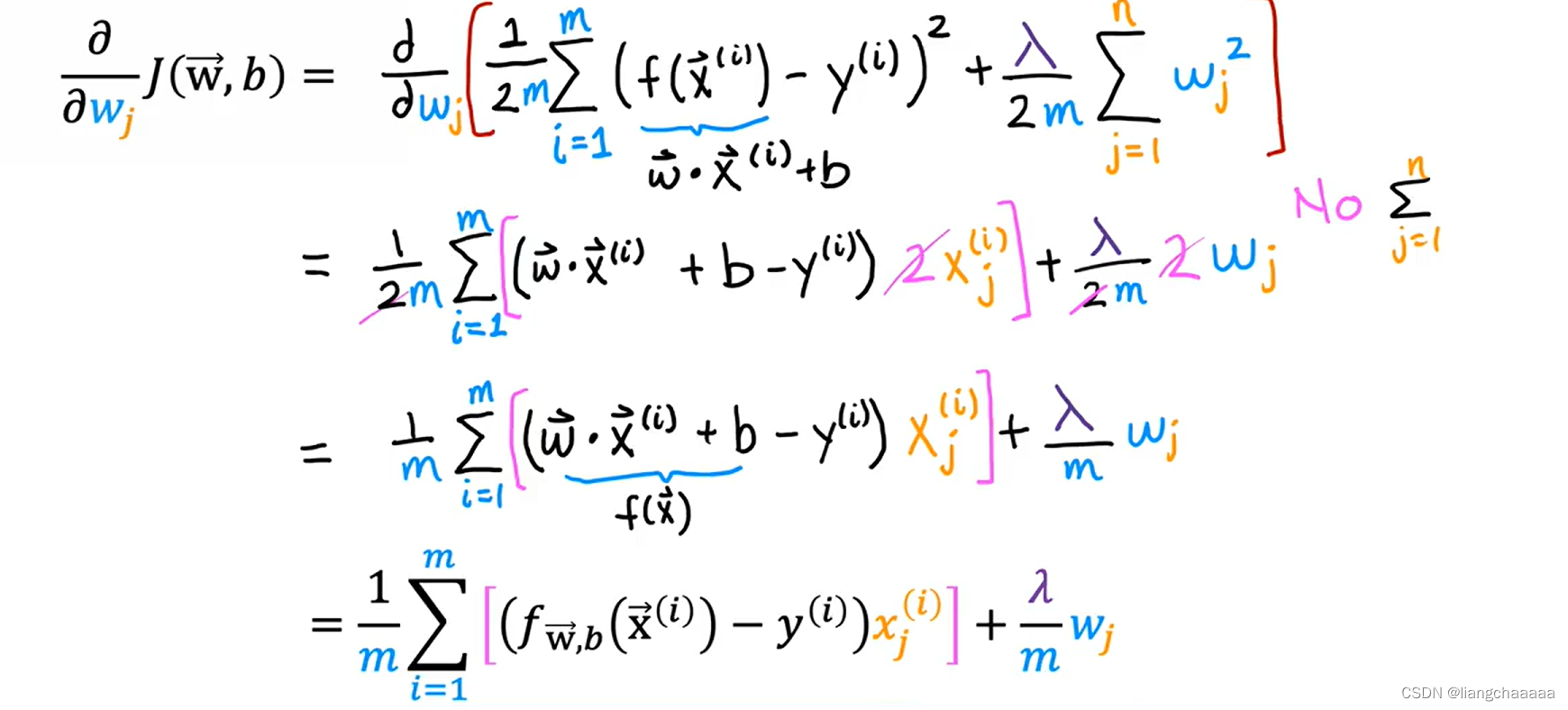
def compute_cost_linear_reg(X, y, w, b, lambda_):
    """
    Computes the cost over all examples
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
      lambda_ (scalar): Controls amount of regularization
    Returns:
      total_cost (scalar):  cost 
    """

    m  = X.shape[0]
    n  = len(w)
    cost = 0.
    for i in range(m):
        f_wb_i = np.dot(X[i], w) + b                                   #(n,)(n,)=scalar, see np.dot
        cost = cost + (f_wb_i - y[i])**2                               #scalar             
    cost = cost / (2 * m)                                              #scalar  
 
    reg_cost = 0
    for j in range(n):
        reg_cost += (w[j]**2)                                          #scalar
    reg_cost = (lambda_/(2*m)) * reg_cost                              #scalar
    
    total_cost = cost + reg_cost                                       #scalar
    return total_cost                                                  #scalar

def compute_gradient_linear_reg(X, y, w, b, lambda_): 
    """
    Computes the gradient for linear regression 
    Args:
      X (ndarray (m,n): Data, m examples with n features
      y (ndarray (m,)): target values
      w (ndarray (n,)): model parameters  
      b (scalar)      : model parameter
      lambda_ (scalar): Controls amount of regularization
      
    Returns:
      dj_dw (ndarray (n,)): The gradient of the cost w.r.t. the parameters w. 
      dj_db (scalar):       The gradient of the cost w.r.t. the parameter b. 
    """
    m,n = X.shape           #(number of examples, number of features)
    dj_dw = np.zeros((n,))
    dj_db = 0.

    for i in range(m):                             
        err = (np.dot(X[i], w) + b) - y[i]                 
        for j in range(n):                         
            dj_dw[j] = dj_dw[j] + err * X[i, j]               
        dj_db = dj_db + err                        
    dj_dw = dj_dw / m                                
    dj_db = dj_db / m   
    
    for j in range(n):
        dj_dw[j] = dj_dw[j] + (lambda_/m) * w[j]

    return dj_db, dj_dw

与之前不同的地方就是计算代价时考虑上了lambda*wj