时距曲线
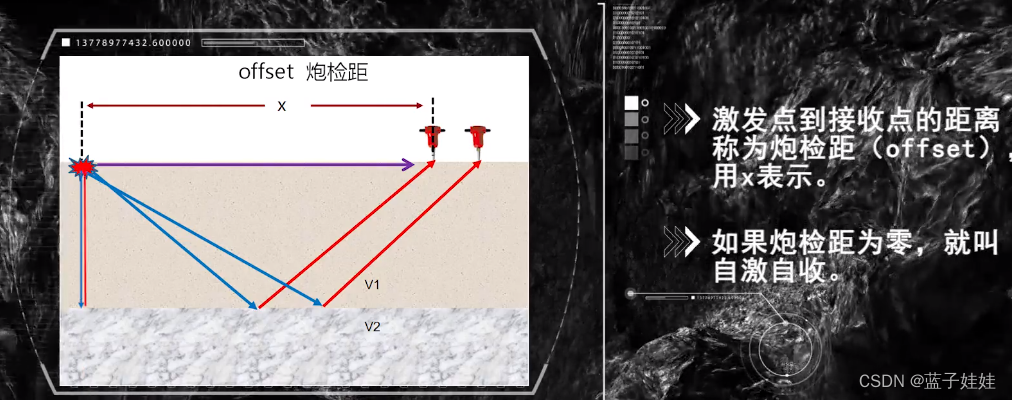
在反射波地震勘探中,一般是在地面激发地面接收,激发点到接受点的距离称为炮间距(offset),用
x
x
x表示。如果炮间距为0,称为自激自收。
单道接收:激发一次只在一个位置上接收地震波。
多道接收:在多个位置上同时接收地震波。可以是单点激发,一边接收;也可以是中点激发,两边接收。
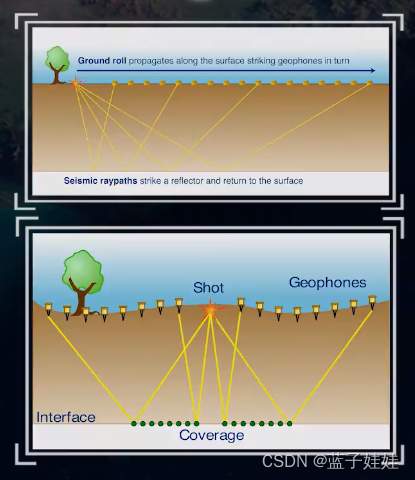
野外如果呈单道接收,自激自收,则记录到的反射波的时间与炮间距无关,只与地下岩石的地质因素有关。
自激自收能够直观反应地下地质情况,但是效率低,费用高且信噪比低。

实际地震观测中,采用一点激发,多道接收的方式。此时,地震波传播时间不仅与地质因素有关,还与炮间距有关。当地质因素不变时,炮间距越大,波的旅行时越长。
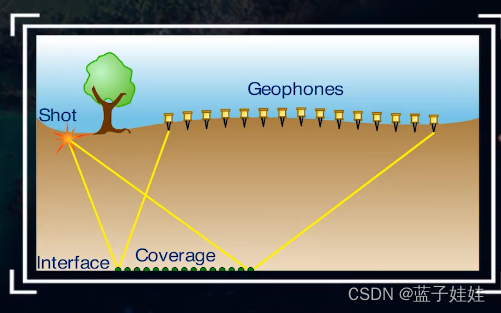
一点激发多道接收的野外观测方式如下:


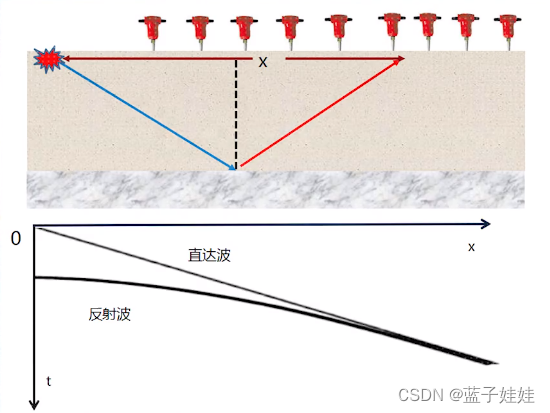
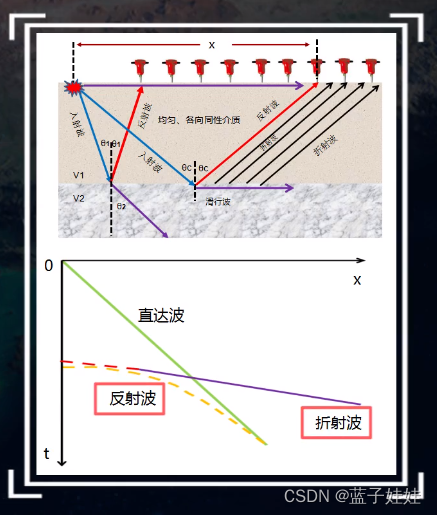
时距曲线:地震波从激发点传播到接收点,所用时间t与炮检距x之间的曲线,通常写作 t=t(x)。地下地质模型不同,地震波类型不同,那么地震时距曲线特点就不同。
直达波时距曲线:直达波是没有遇到反射界面,直接从激发点传播到接收点的地震波。假设地下介质是均匀各向同性的,一点激发多道接收,而且激发点和多个接收点的连线在一条直线上,则共炮点的直达波的传播时间就是炮间距x除以传播速度v。直达波的时距曲线是一条过炮点的直线,直线的斜率是1/v.
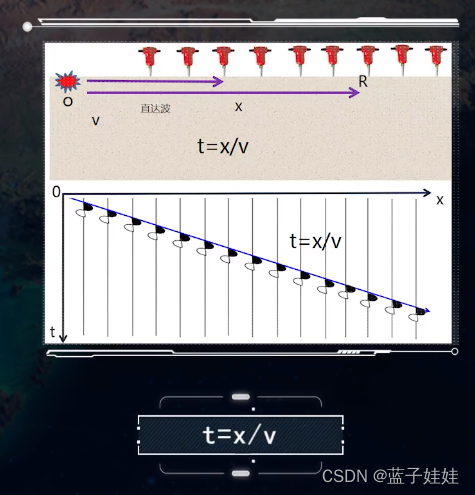
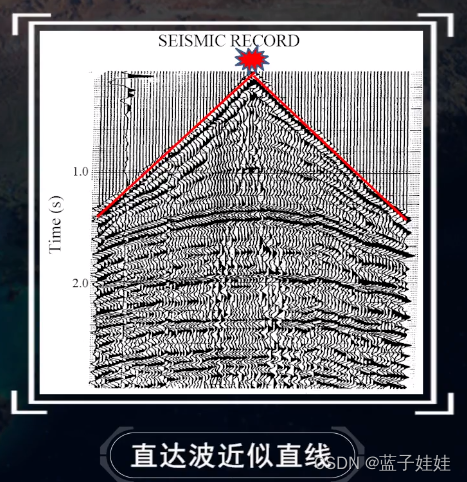
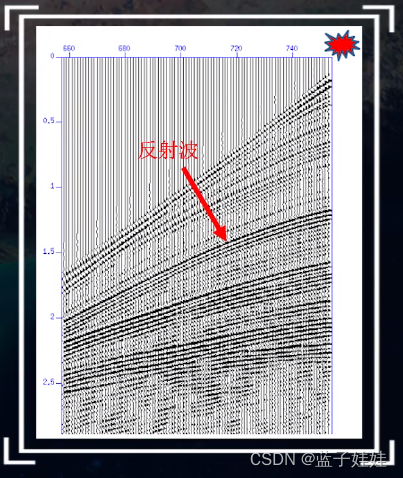
如果一点激发,单边多道接收,在野外地震记录上就可以观测到直达波,它就是一条过炮点的直线。
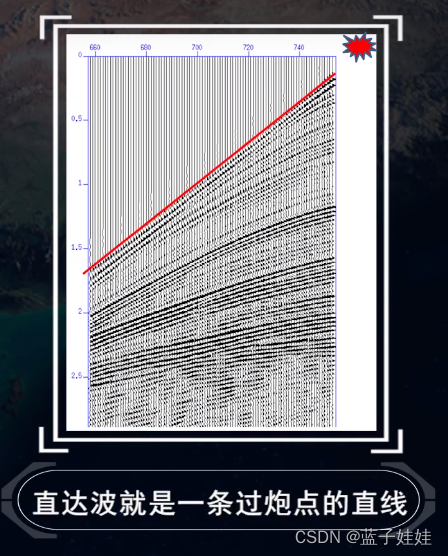
如果是中点激发,两边多道接收,直达波的时距曲线就是两条过炮点的直线。
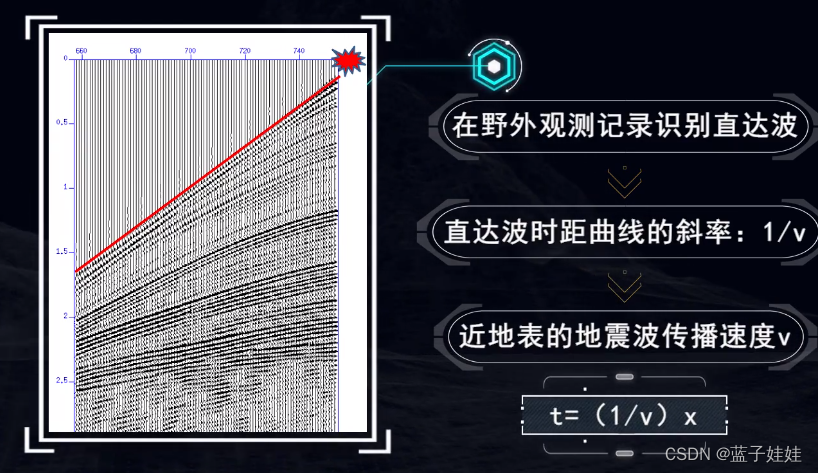
在野外地震记录中,可以识别出直达波就可以求出直达波的时距曲线的斜率 1/v,那么可以求出近地表的地震波传播速度 v。
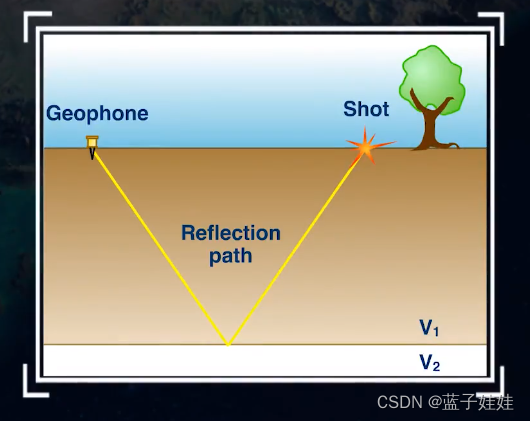
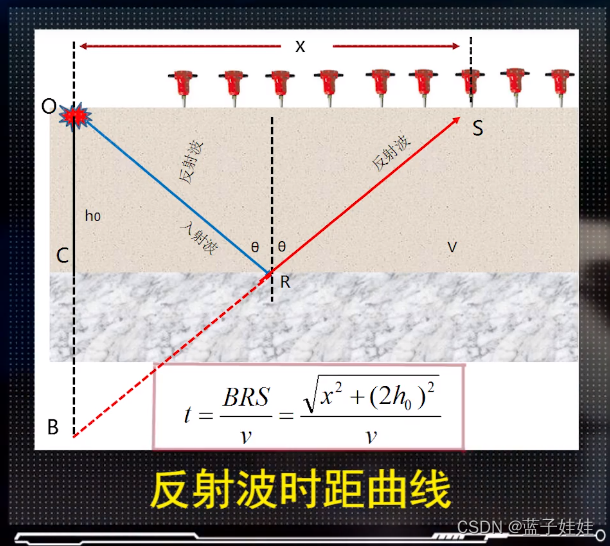
反射波的时距曲线:假设地下有一个水平的反射界面,且界面上下有波阻抗的差异,界面以上是均匀各向同性地层。如图所示,在O点激发地震波,波传播到R点产生反射,在地面上炮检距为X的S点接收到。我们可以证明地震波沿着ORS所传播的时间相当于从对称于界面的虚震源B点出发,沿着BRS所传播的时间。
t
=
B
R
S
v
=
x
2
+
(
2
h
0
)
2
v
,
t
2
=
t
0
2
+
x
2
v
2
,
t
0
=
2
h
0
v
为自激自收时间
t = \frac{BRS}{v} = \frac{\sqrt{x^2 + (2h_0)^2}}{v}, \\ t^2 = t_0^2 + \frac{x^2}{v^2},\\ t_0 = \frac{2h_0}{v} 为自激自收时间
t=vBRS=vx2+(2h0)2,t2=t02+v2x2,t0=v2h0为自激自收时间
它可以被整理为双曲线方程
t
2
t
0
2
−
x
2
(
t
0
v
)
2
=
1
\frac{t^2}{t_0^2} - \frac{x^2}{(t_0 v)^2} = 1
t02t2−(t0v)2x2=1.
因此,单点激发共炮点的反射波的时距曲线就是一条四分之一双曲线。
那么中点激发两边多道接收的反射波的时局曲线为二分之一双曲线。
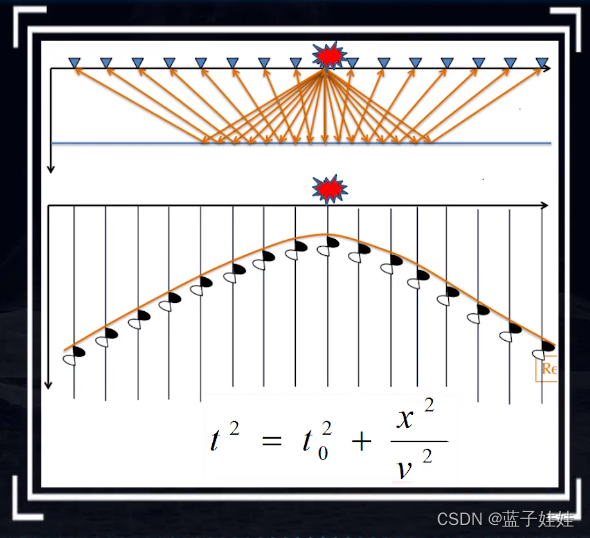
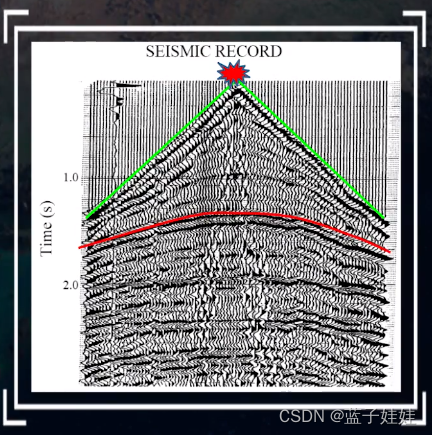
反射波时距曲线的极小点在激发点的正下方,相当于地震波自激自收的时间
t
0
t_0
t0,其次,直达波的时距曲线刚好是反射波时距曲线的渐近线。
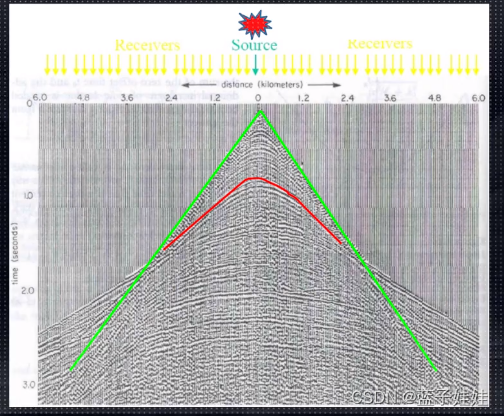
折射波时距曲线:当地震波入射角达到临界角的时候会产生滑行波,根据惠更斯原理进而产生折射波。入射波时间为
T
O
A
T_{OA}
TOA,滑行波时间为
T
A
B
T_{AB}
TAB,折射波时间为
T
B
S
T_{BS}
TBS。
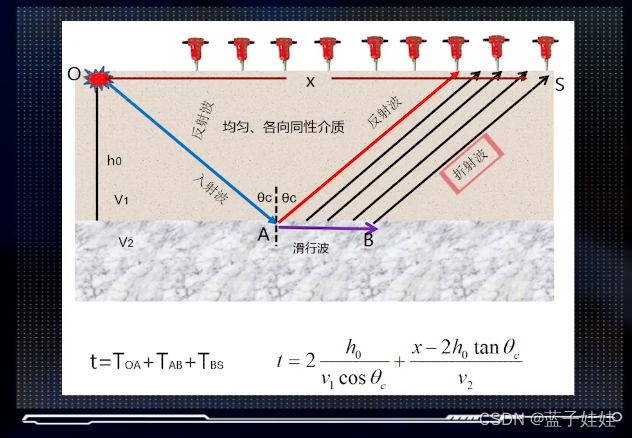
将折射波的时距曲线进一步整理为直线方程
t
=
2
h
0
cos
θ
c
v
1
+
1
v
2
x
t = \frac{2h_0 \cos \theta_c}{v_1} + \frac{1}{v_2} x
t=v12h0cosθc+v21x。折射波是一条直线,其斜率为折射界面下面地层速度的倒数。
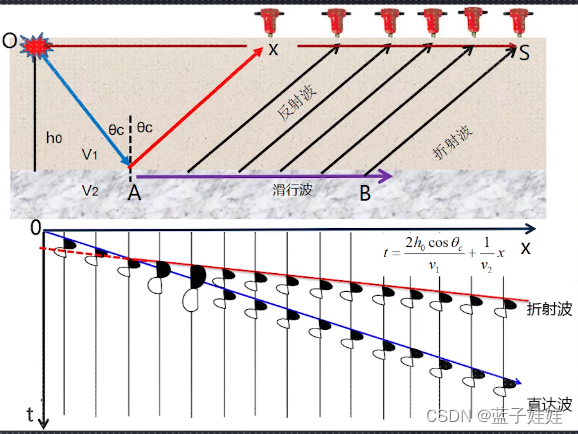
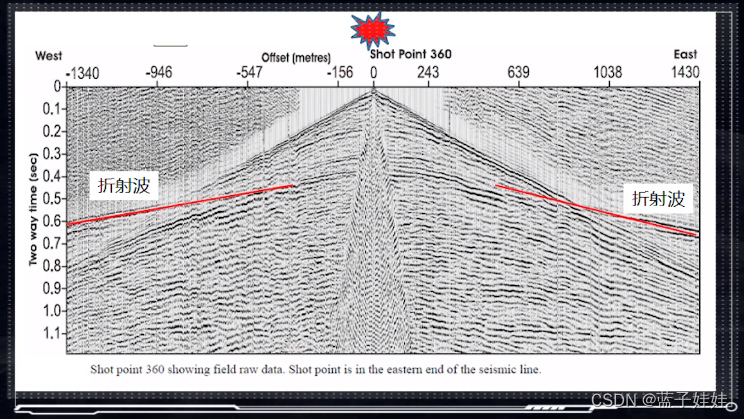
从下图可知,折射波和直达波是相交的,利用该交点,可以求出折射界面的埋藏深度,也可以证明折射波和反射波时距曲线是相切的。
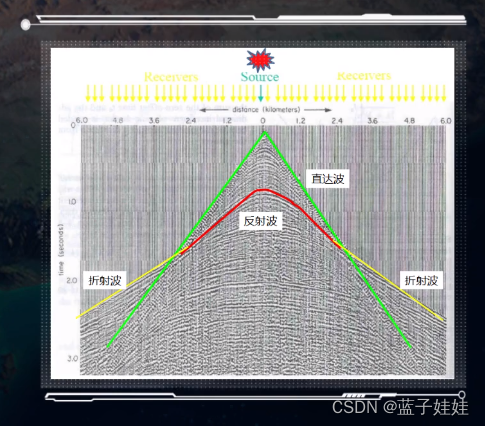
复杂介质的地震时距曲线
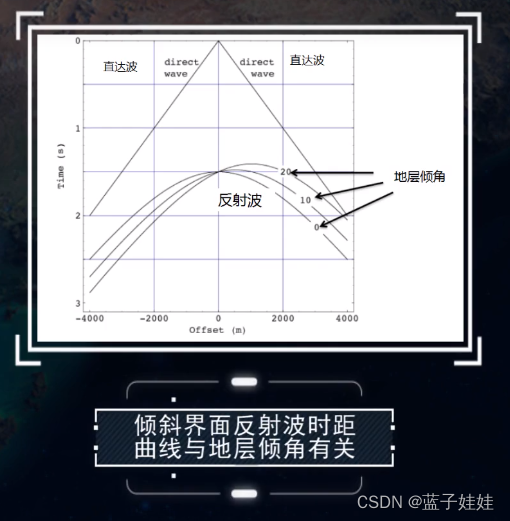
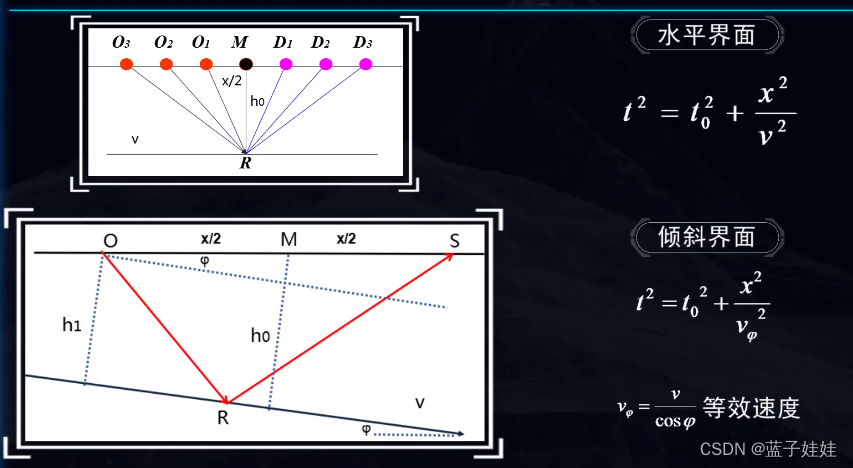
- 倾斜界面情况下的反射波时距曲线。如下图所示,地下有一倾斜反射界面(倾角为
ϕ
\phi
ϕ),界面上的地层是均匀各向同性的,速度是
v
v
v,震源O点激发的地震波入射到倾斜界面上,在R点产生反射,在炮检距为X的S点接收到,ORS传播的时间相当于从对称倾斜界面的虚震源D点,沿着DRS传播的时间。假设D到地面的垂直投影为m点,m点到震源O的距离为
X
m
X_m
Xm,震源O到倾斜界面的法线深度为h,那么倾斜界面地震反射波时距曲线的方程表示为
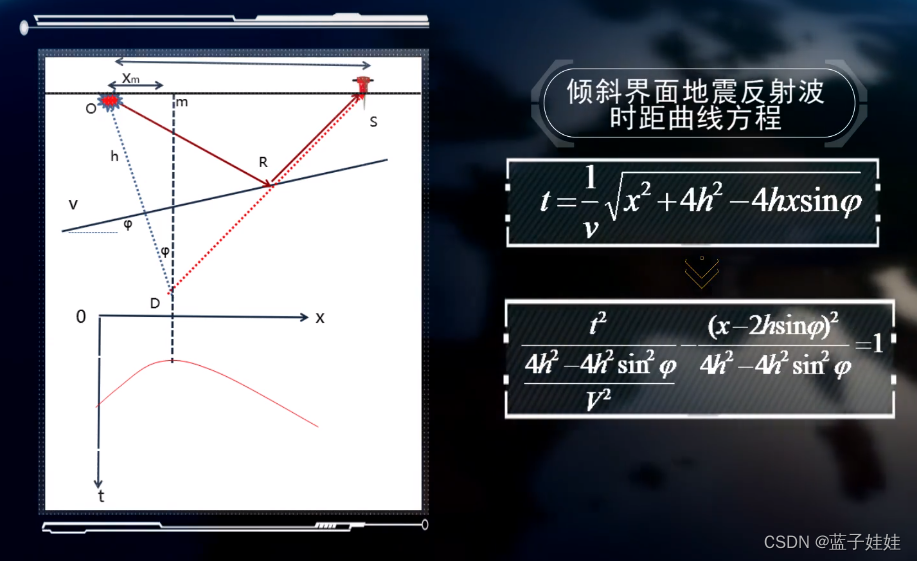
倾斜界面地震反射波时距曲线仍然是一个双曲线,但是双曲线的极小点在 x = 2 h sin ϕ x = 2h\sin \phi x=2hsinϕ,在虚震源的正下方。
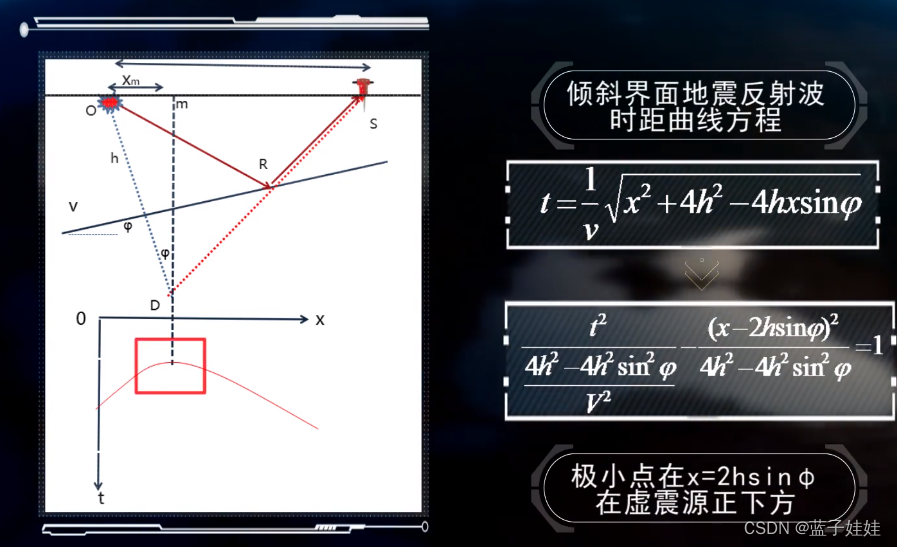
从倾斜界面共炮点地震记录可知,双曲线的极小点不在震源的正下方。
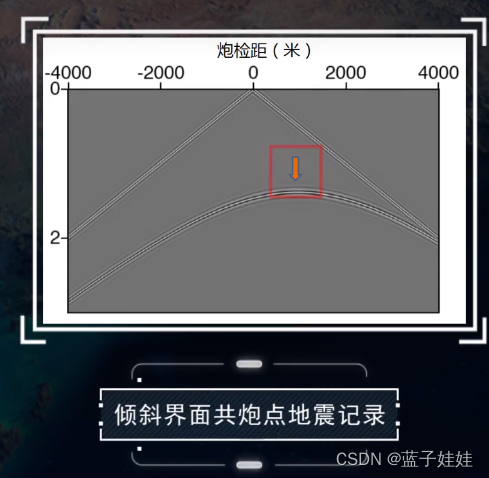
倾斜界面情况下,反射波的时距曲线与地层倾角有关。倾角越大,极小点偏离震源越远。
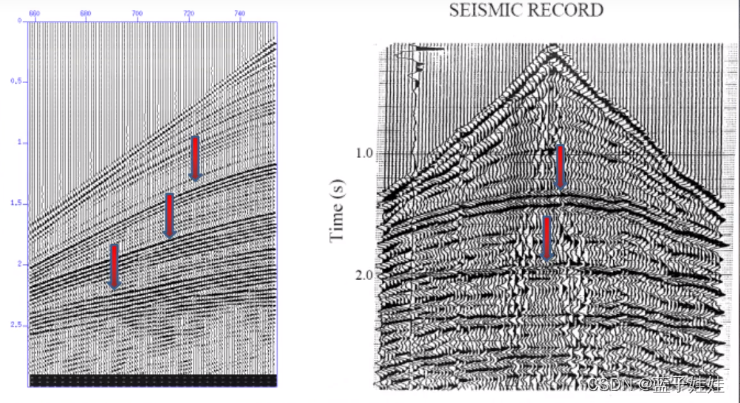
在水平层状地层情况下,炮检距X不大时,共炮点反射波时距曲线可以近似看成是双曲线。
如果对反射波的旅行时求导可以发现,对某一固定的
x
x
x点,
h
h
h越小,
d
t
d
x
\frac{dt}{dx}
dxdt 越大,曲线越陡。
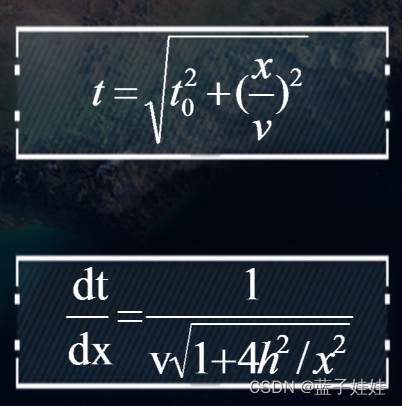
因此,浅层反射波的时距曲线比深层的要陡。
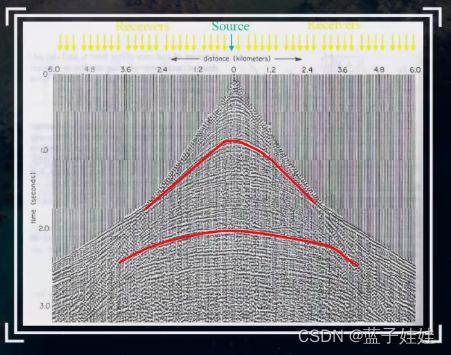
对于更复杂的地下介质,上述介绍的时距曲线都不能描述地震波的真实传播。可以采用射线追踪模拟复杂的地下介质;
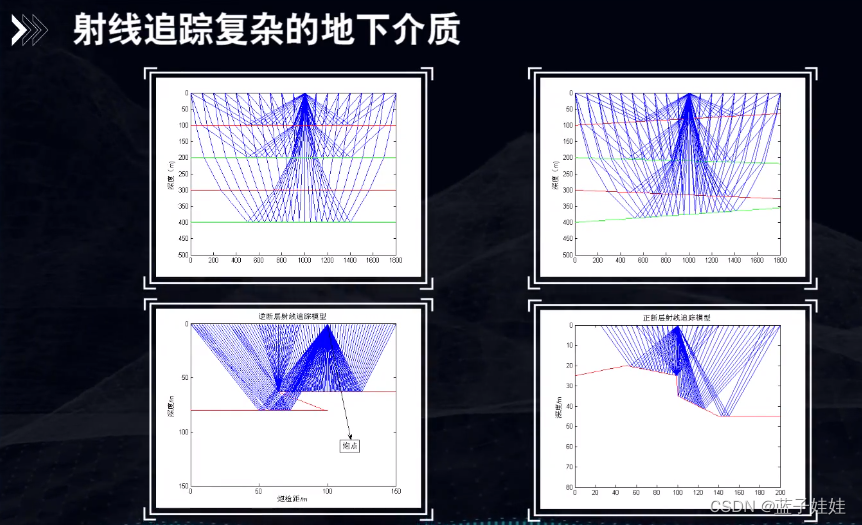
还可以利用波动方程模拟复杂的地下介质。
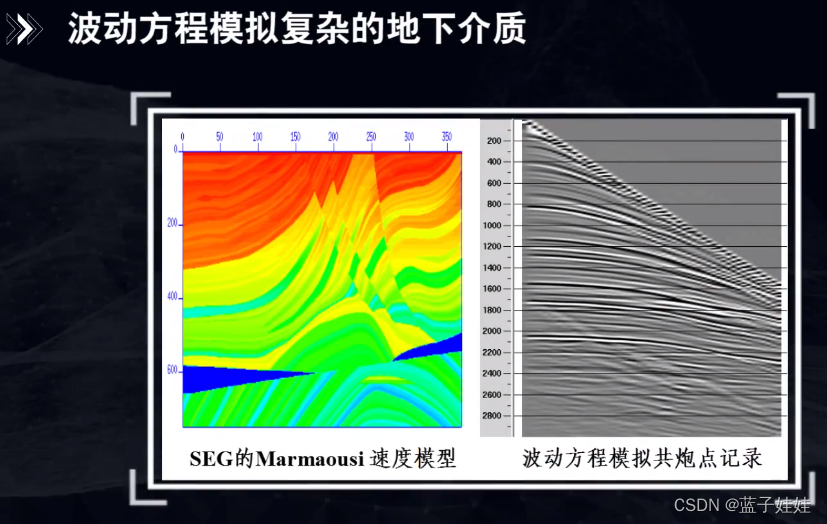
如果地震波在传播过程中遇到诸如尖灭,断层,不整合等不连续点时,根据惠更斯原理会产生绕射波。
如下图所示,假设有一个直立断层,断点R在地面的投影为R’,R’到激发点O的距离为L,O点激发的地震波入射到R点,除了产生反射波还会产生绕射波。炮检距为x的接收点可以接收来自R点的绕射波。
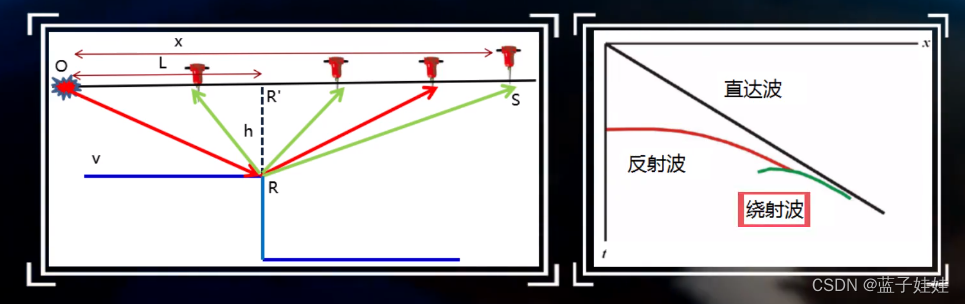
那么,绕射波的传播时间可以表示为
t
R
=
1
v
(
L
2
+
h
2
+
(
x
−
L
)
2
+
h
2
)
t_R = \frac{1}{v} (\sqrt{L^2 + h^2} + \sqrt{(x - L)^2 + h^2})
tR=v1(L2+h2+(x−L)2+h2)
可以证明该时距曲线也是双曲线。绕射波的时距曲线和反射波的时距曲线在断点处是相切的。
在均匀介质情况下,直达波的时距曲线是直线。如果地震波速度随深度连续变化或者激发点和多个接收点的连线不在一条直线上,直达波的时距曲线就不是直线。
均匀介质情况下,一个水平折射界面的折射波的时距曲线是直线。在水平层状地层中,满足产生折射波条件的情况下,折射波的时距曲线可以证明仍然是直线。利用这些直线方程的斜率和截距就可以求出折射层的厚度和速度。
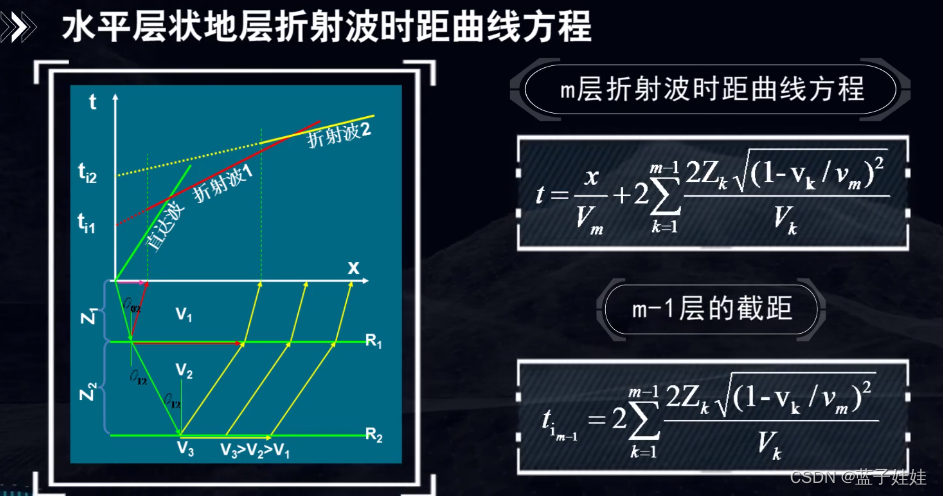
在倾斜界面情况下,折射波的时距曲线也是直线。
共中心点记录的时距曲线
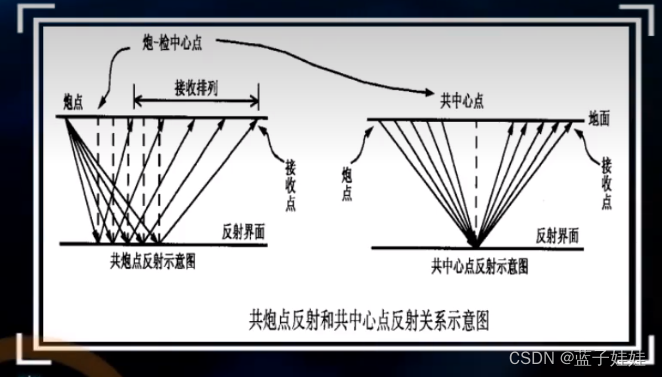
从1956年开始至今,地震勘探一直采用多次覆盖观测系统,只要合理布置激发点和接收点的位置,就可以对地下同一反射点进行多次观测。

在水平界面情况下,激发点和接收点的中点刚好是地下反射点在地面的投影点,因此,地震多次覆盖技术也叫共中心点(CMP)技术。
如下图所示,如果在
O
1
O_1
O1点激发,
D
1
D_1
D1点接收,可以接收到来自地下一个水平界面上R点的反射,在
O
2
O_2
O2点激发,
D
2
D_2
D2点接收,也可以接收到来自R点的反射。在
O
3
O_3
O3点激发,
D
3
D_3
D3点接收,也可以接收到来自R点的反射。这样就对R点进行了三次观测,而且共同一个中心点,共同一个反射点。
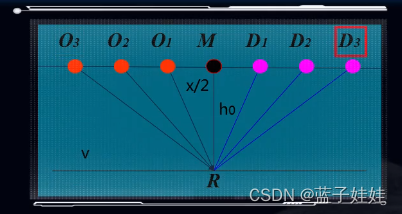
那么,共中心点记录的反射波时距曲线可以表示为
t
=
2
v
(
x
2
)
2
+
h
0
2
,
t
2
=
t
0
2
+
x
2
v
2
,
t
0
=
2
h
0
v
为共中心点自激自收的时间
.
t = \frac{2}{v} \sqrt{(\frac{x}{2})^2 + h_0^2}, \\ t^2 = t_0^2 + \frac{x^2}{v^2}, \\ t_0 = \frac{2h_0}{v} 为共中心点自激自收的时间.
t=v2(2x)2+h02,t2=t02+v2x2,t0=v2h0为共中心点自激自收的时间.
那么,共中心点时距曲线是一条双曲线,极小点在共中心点的正下方。
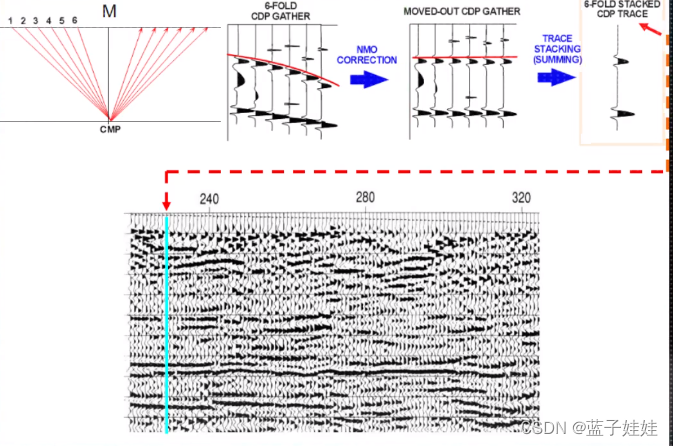
一个共中心点道集的记录是由来自对称于同一个中心点的不同炮不同道的记录组成,这个过程称为抽道集。共中心点道集的记录不能马上叠加,需要消除炮检距引起的时差,然后才能叠加。这起到提高信噪比的作用。
共中心点时距曲线与共炮点时距曲线的区别:
相同点:时距曲线都是双曲线。
- 共中心点时距曲线:只反映界面上一个点。 t 0 t_0 t0 是共中心点的垂直时间,X是接收点到不同炮的距离。
- 共炮点时距曲线:反映的是一段反射界面, t 0 t_0 t0 是激发点的垂直时间,X是接收点到同一炮的距离。
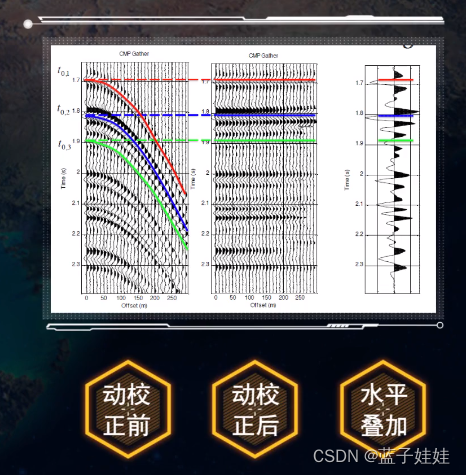
动校正量:在水平界面情况下,共中心点道集中反射波时间与中心点自激自收的时间之差纯粹是由炮检距引起的时差,称为正常时差或者动校正量
Δ
t
\Delta t
Δt.
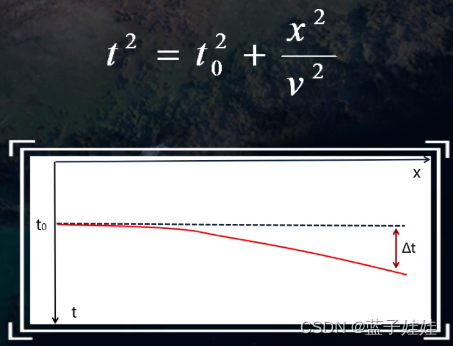
Δ
t
=
t
−
t
0
=
(
x
v
)
2
+
t
0
2
−
t
0
.
Δ
t
≈
x
2
2
v
2
t
0
\Delta t = t - t_0 = \sqrt{(\frac{x}{v})^2 + t_0^2} - t_0. \\ \Delta t \approx \frac{x^2}{2 v^2 t_0}
Δt=t−t0=(vx)2+t02−t0.Δt≈2v2t0x2
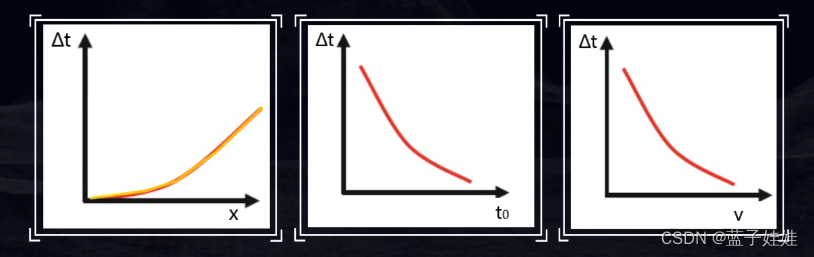
动校正(NMO):从共中心点反射波时距曲线中减去动校正量的过程称为动校正。动校正后,时距曲线变成了直线,就可以同向叠加,来提高信噪比。
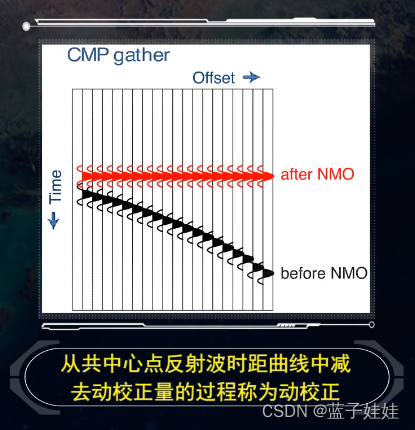
在水平层状地层共中心点反射波时距曲线中,它也是近似的双曲线,其时距曲线方程不同的是速度使用的是均方根速度
v
r
m
v_{rm}
vrm,表示为
t
2
=
t
0
2
+
x
2
v
r
m
2
.
t^2 = t_0^2 + \frac{x^2}{v_{rm}^2}.
t2=t02+vrm2x2.
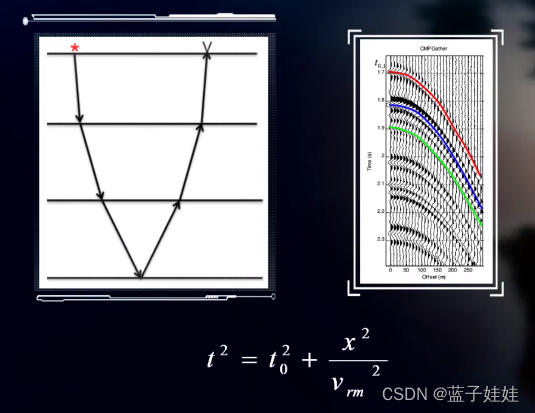
三层层状介质动校正后如下图所示。

在水平层状介质情况下,共中心点道集经过动校正后就可以进行水平叠加。
假设有一倾斜的反射界面(倾角为
ϕ
\phi
ϕ),在O点激发,S点接收,激发点和接收点的中点为M,激发点O到界面的法线深度为
h
1
h_1
h1,中点M到界面的法线深度为
h
0
h_0
h0。从O点激发的地震波在R点反射后,在S点接收到的传播时间和倾斜界面情况下共炮点反射波时距曲线是一样的公式。
t
=
1
V
x
2
+
4
h
1
2
+
4
h
1
x
sin
ϕ
t = \frac{1}{V}\sqrt{x^2 + 4h_1^2 + 4h_1 x \sin \phi}
t=V1x2+4h12+4h1xsinϕ
只需要将上述公式中的
h
1
h_1
h1替换为
h
0
−
x
2
sin
ϕ
h_0 - \frac{x}{2} \sin \phi
h0−2xsinϕ,表示为
t
=
1
V
4
h
0
2
+
x
2
cos
2
ϕ
t = \frac{1}{V}\sqrt{4h_0^2 + x^2 \cos ^2 \phi }
t=V14h02+x2cos2ϕ

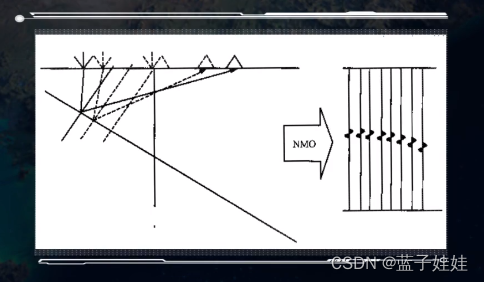
水平界面个倾斜界面的共中心点时距曲线对比如下:
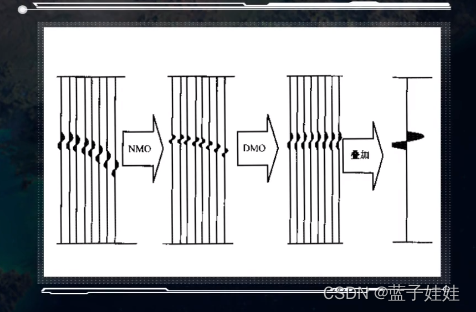
由于在倾斜界面下,共了中心点没有共反射点,所以经过正常的动校正(NMO)后不是一条直线。
如果再进行倾角时差(DMO)校正后,就可以校正为一条直线,实现同向叠加。

![【群智能算法改进】一种改进的沙丘猫群优化算法 改进沙丘猫群算法 改进SCSO[2]【Matlab代码#36】](https://img-blog.csdnimg.cn/a3ac2ba116364ae4a01e3847ed1a52b0.png#pic_center)