前言

因为二叉树是一种特殊的树，所以想要学习好二叉树，必须了解树型结构，知道树的基本概念。所以正式开始学习之前，在前面为大家引入了树的概念。

1. 树型结构

1. 1 树的概念

树是一种非线性的数据结构，它是有n个节点构成的集合，把它称为树，是因为这种结构看起来就像一个倒挂的树，根在上面，叶在下面。

1.2 树的特点

• 有一个特殊的节点，没有前驱节点，我们将此称为根节点。
• 树是递归定义的。
• 树的任何节点都可以有任意后继，但是它们不会交叉。
• 树是一个非线性数据结构。

1.3 树的相关术语

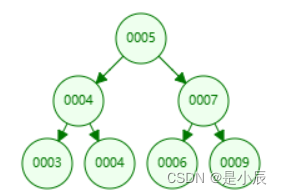
• 根节点：一个特殊节点，没有前驱节点；上图：第一个1 。
• 节点的度：一个节点拥有的子树的多少，就是该节点的度；上图：9的度为：2 。
• 树的度：一棵树最大节点的度就是树的度； 上图：最大的节点的度为3 ，则树的度为3 。
• 叶节点：又称叶子节点，终端节点，度为零的节点；上图：3、4等都是叶节点。
• 父节点：又称双亲节点，父亲节点，一个节点有子节点，则就是这是字节点的父节点；上图：9是3的父节点。
• 子节点：又称孩子节点，一个节点下面与连接的节点就是子节点；上图：3是9的子节点。
• 节点的层次：根节点为第一层，根节点的子节点为第二层，以此类推。
• 树的高度或深度：树中最大的节点的层次。

2. 二叉树（binary tree）

2.1 二叉树的概念

二叉树是一种树形数据结构，是一种特殊的树，二叉树中每个节点最多只能有两个子节点，并且二叉树的次序是不可颠倒的，是一颗有序树。

2.2 二叉树中的特殊树

二叉树是一种特殊的树，而特殊树中还会有特殊。

2.2.1 满二叉树

一棵二叉树，如果每层的结点数都达到最大值，则这棵二叉树就是满二叉树。也就是说，如果一棵
二叉树的层数为K，且结点总数是 ，则它就是满二叉树。

2.2.2 完全二叉树

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K的，有n
个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从0至n-1的结点一一对应时称之为完全二叉树。 要注意的是满二叉树是一种特殊的完全二叉树。

2.3 二叉树的性质

1. 二叉树是由节点和边构成的树形结构，每个节点最多有两个子节点，分别称为左子节点和右子节点，没有子节点的节点称为叶子节点。
2. 二叉树有一个根节点，其它节点都是根节点的子节点。根节点没有父节点。
3. 对于一个有n个节点的二叉树，设其高度为h，则h的取值范围为1到n，且h为log2(n+1)向上取整。
4. 在二叉树的第i层上，最多有2^(i-1)个节点。
5. 若深度为h的二叉树满足：每个节点都有两个子节点，且所有叶子节点都在第h层或h-1层，则称该树为满二叉树。满二叉树的节点数为2^h-1。
6. 若深度为h的二叉树最后一层只有叶子节点，其它层都是满的，则称该树为完全二叉树。完全二叉树的节点数在1到2^(h-1)之间。
7. 若二叉树的左右子树可以交换位置且仍为同一棵树，则该二叉树为镜像二叉树。1. 二叉树是由节点和边构成的树形结构，每个节点最多有两个子节点，分别称为左子节点和右子节点，没有子节点的节点称为叶子节点。
   《一些练习的题》
   1.某二叉树共有 399 个结点，其中有 199 个度为 2 的结点，则该二叉树中的叶子结点数为（ ）
   A 不存在这样的二叉树
   B 200
   C 198
   D 199
   2.在具有 2n 个结点的完全二叉树中，叶子结点个数为（ ）
   A n
   B n+1
   C n-1
   D n/2
   3.一个具有767个节点的完全二叉树，其叶子节点个数为（）
   A 383
   B 384
   C 385
   D 386
   4.一棵完全二叉树的节点数为531个，那么这棵树的高度为（ ）
   A 11
   B 10
   C 8
   D 12
   答案：
   1.B
   2.A
   3.B
   4.B

3. 二叉树的遍历

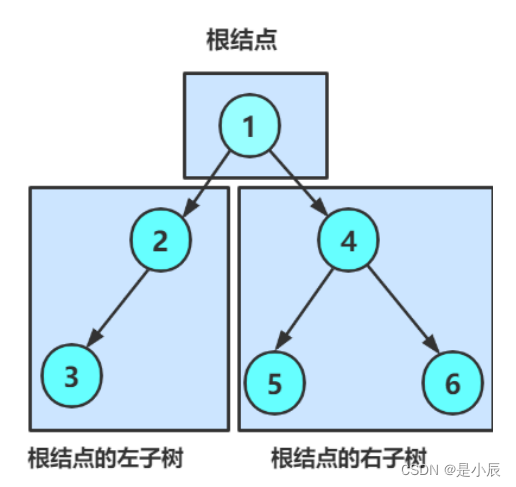
二叉树的遍历是一个重要的点，是一个必须要掌握的点，遍历分为前中后序遍历，层序遍历四种。我们将使用这张图详细介绍一下。
遍历(Traversal)是指沿着某条搜索路线，依次对树中每个结点均做一次且仅做一次访问。访问结点所做的操作依赖于具体的应用问题。
遍历是二叉树上最重要的操作之一，是二叉树上进行其它运算之基础。

3.1 前序遍历

前序遍历的遍历顺序：访问根结点—>根的左子树—>根的右子树。
遍历结果：123456

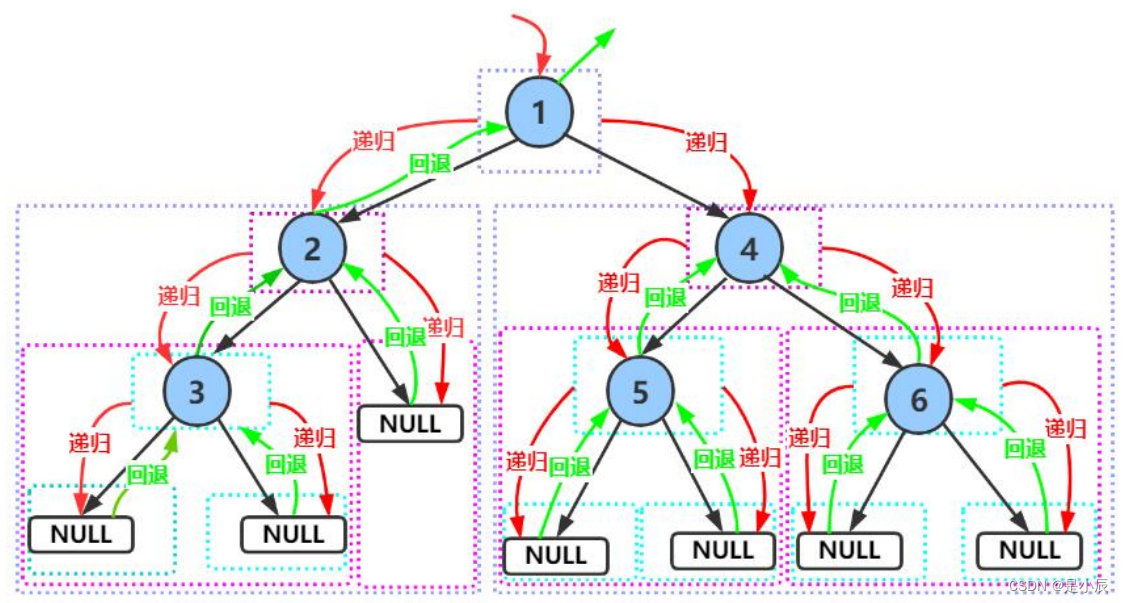
如上图：遍历根节点1，然后遍历左子树2，一直遍历到左子树为null。然后返回途中遍历右子树，3的右子树为null。然后返回到2，2的右子树为null，返回到根节点1。1的左树已经遍历一遍，所以继续遍历1的右子树4，然后先遍历左子树5，5的左右都为空，则返回遍历4的右子树6。6的左右都为空，原路返回，到根节点遍历结束。

3.2 中序遍历

根的左子树—>根节点—>根的右子树。
遍历结果：321546

3.3 后序遍历

根的左子树—>根的右子树—>根节点。
遍历结果：325641

3.4 层序遍历

除了先序遍历、中序遍历、后序遍历外，还可以对二叉树进行层序遍历。设二叉树的根节点所在
层数为1，层序遍历就是从所在二叉树的根节点出发，首先访问第一层的树根节点，然后从左到右访问第2层上的节点，接着是第三层的节点，以此类推，自上而下，自左至右逐层访问树的结点的过程就是层序遍历。
遍历结果：124356

一些练习选择题

1. 某完全二叉树按层次输出（同一层从左到右）的序列为 ABCDEFGH 。该完全二叉树的前序序列为()
   A: ABDHECFG B: ABCDEFGH C: HDBEAFCG D: HDEBFGCA
2. 二叉树的先序遍历和中序遍历如下：先序遍历：EFHIGJK;中序遍历：HFIEJKG.则二叉树根结点为()
   A: E B: F C: G D: H
3. 设一课二叉树的中序遍历序列：badce，后序遍历序列：bdeca，则二叉树前序遍历序列为()
   A: adbce B: decab C: debac D: abcde
4. 某二叉树的后序遍历序列与中序遍历序列相同，均为 ABCDEF ，则按层次输出(同一层从左到右)的序列为()
   A: FEDCBA B: CBAFED C: DEFCBA D: ABCDEF
   【参考答案】 1. A 2. A 3. D 4. A

总结

这篇博客主要为大家带来树及二叉树的基本概念，性质，遍历方式等，下篇博客将为大家带来代码的实现以及应用。
期待大家关注!
最后，祝大家61快乐，天天开心！