目录
一.堆
1.1堆的概念
1.2堆的存储方式
1.3堆的操作
1.3.1堆的创建
1.3.2代码的实现:
堆的插入元素
堆的删除
二、PriorityQueue
2.1概念
2.2性质
2.3PriorityQueue的创建构造
2.4PriorityQueue的操作方法
总结
😽个人主页:tq02的博客_CSDN博客-C语言,Java,Java数据结构领域博主
🌈梦的目标:努力学习,向Java进发,拼搏一切,让自己的未来不会有遗憾。
🎁欢迎各位→点赞👍 + 收藏⭐ + 评论📝+关注✨
本章讲解内容:堆与PriorityQueue 基于二叉树的知识。
来源于百度 使用编译器:IDEA
一.堆
1.1堆的概念
堆,也称优先级队列,是存放元素的集合。而所存放的元素按照 完全二叉树的顺序存储方式。堆中每个结点总是 不大于或不小于 其父结点。
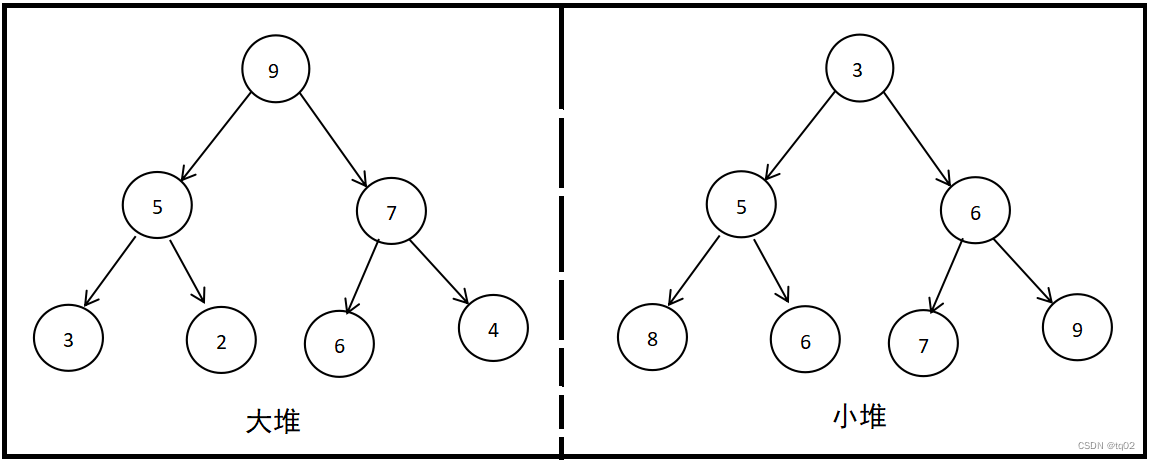
堆分为2种:大堆 小堆
大堆: 父结点的值 大于 子结点,也就是根结点的值最大。
小堆: 父结点的值 小于 子结点,也就是根结点的值最小。
1.2堆的存储方式
虽然堆的存储方式按照完全二叉树,完全二叉树实现有2种方式(链表 或者 数组)。而此时因为堆的性质,使用一维数组的方式存储更为高效。堆中元素层序存储到一维数组。
代码实现:
public class MyHeap{
public int[] array;
public int capacity; //数组容量
public int index; //数组大小
MyHeap(){
array=new int[10];
this.capacity=10;
this.index=0;
}
MyHeap(int num)
{
array=new int[num];
this.capacity=num;
this.index=0;
}
//向下调整结点方法
public void shiftDown(int[] array, int parent);
//插入新元素
public void shiftUp(int[] array,int child);
//删除堆顶元素
public void delectHeap(int[] array);
1.3堆的操作
在使用Java语言操作 堆 之前,我们需要明确几个性质。
1、堆是完全二叉树,除了最后一层,每一层的结点都是满的。
2、当序号为 i 时
- 如果i为0,则为根结点,否则i节点的父节点为 (i - 1)/2;
- 如果2 * i + 1 小于节点个数,则节点i的左孩子下标为2 * i + 1,否则没有左孩子
- 如果2 * i + 2 小于节点个数,则节点i的右孩子下标为2 * i + 2,否则没有右孩子
1.3.1堆的创建
在堆中,我们很明显是需要将一个集合,变成大堆,或者小堆的。
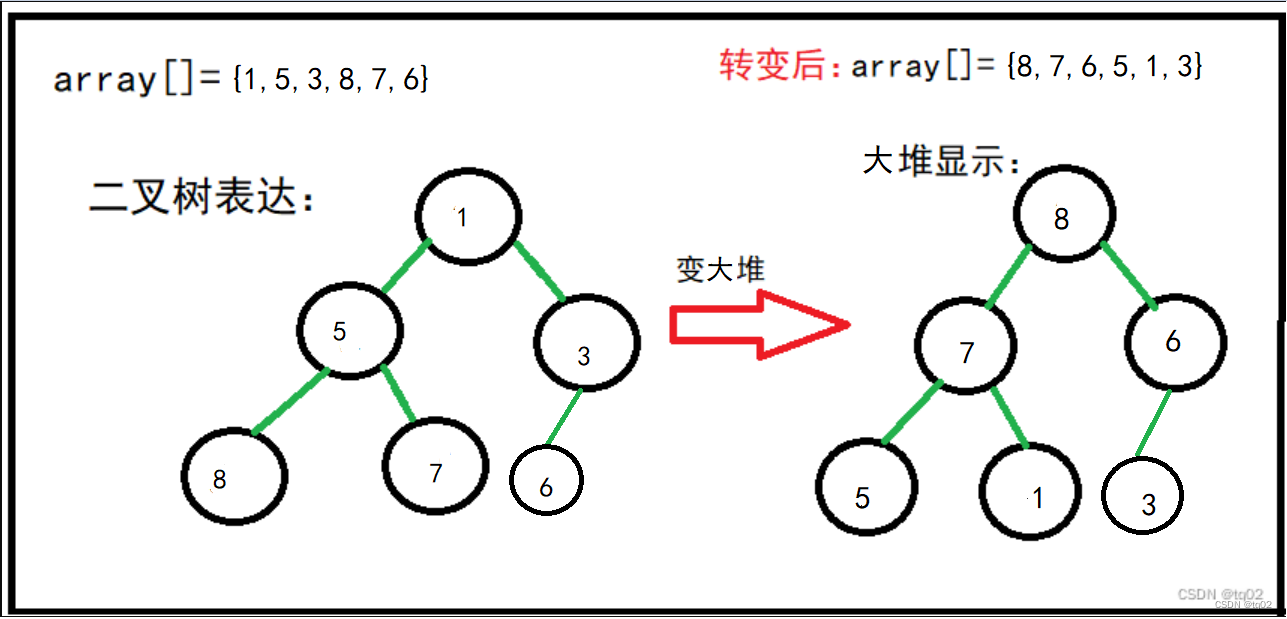
此刻我们展开一下变大堆的过程:
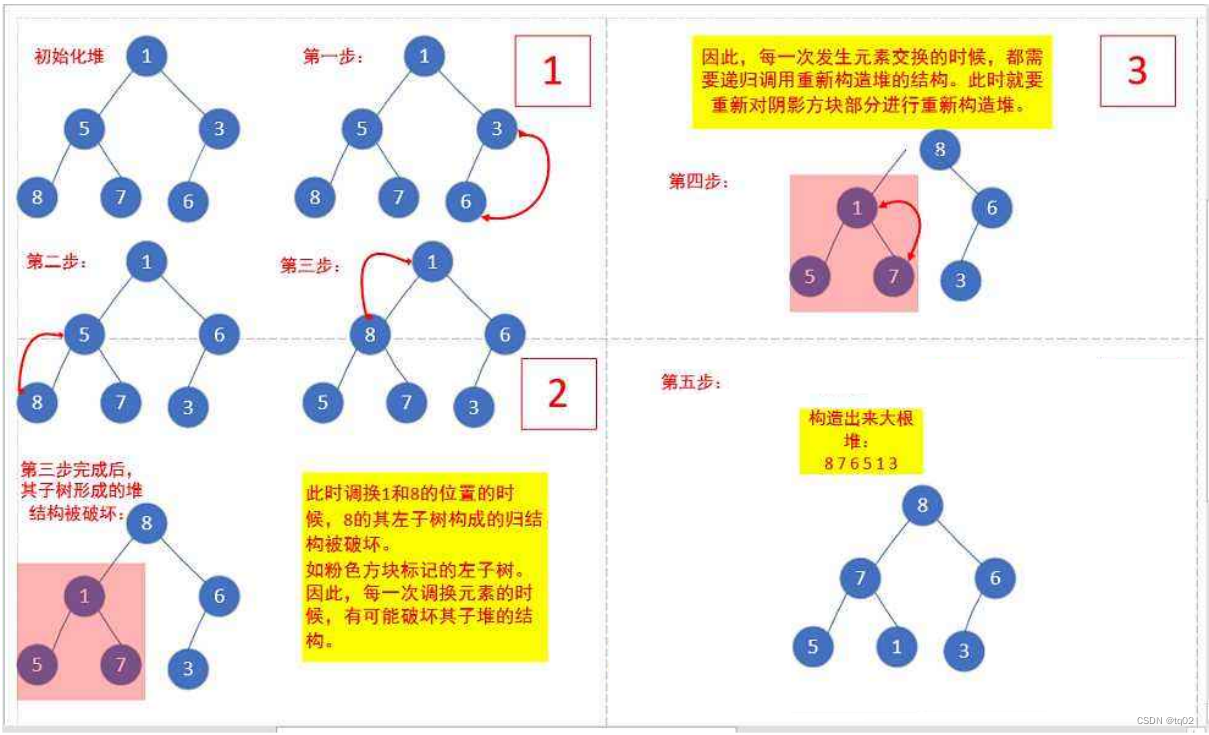
解析:创建大堆,方法:每个子树变成大堆。
1. 让parent标记最后一个结点的父结点,child标记parent的左孩子(注意:parent如果有孩子一定先是有左孩子)
2. 如果parent的左孩子存在,即:child < size(数组长度),进行以下操作,直到parent的左孩子不存在
- parent右孩子是否存在,存在找到左右孩子中最大的孩子,让child进行标记
- 将parent与较大的孩子child比较,如果:
parent小于较大的孩子child,调整结束
否则:交换parent与较大的孩子child,交换完成之后,parent中大的元素向下移动,可能 导致子树不满足对的性质,因此需要继续向下调整,即parent = child;child = parent*2+1; 然后继续2.
1.3.2代码的实现:
//向下调整结点方法
public void shiftDown(int[] array, int parent) {
// child先标记parent的左孩子,因为parent可能右左没有右
int child = 2 * parent + 1;
int size = array.length;
while (child < size) {
// 如果右孩子存在,找到左右孩子中较小的孩子,用child进行标记
if(child+1 < size && array[child+1] > array[child]){
child += 1;
}
// 如果双亲比其最大的孩子小,说明该结构已经满足堆的特性了
if (array[parent] >= array[child]) {
break;
}else{
int t = array[parent]; //将双亲与较大的孩子交换
array[parent] = array[child];
array[child] = t;
// parent中大的元素往下移动,可能会造成子树不满足堆的性质,因此需要继续向下调整
parent = child;
child = parent * 2 + 1;
}
}
}
public void heapJust(int[] array)
{
for(int i=(array.length-1-1)/2;i>=0;i--)
{
shiftDown(array,i);
}
}堆的插入元素
1. 先将元素放入到数组的最后一位中(二叉树的末端)(注意:空间不够时需要扩容)
2. 将最后新插入的节点向上调整,直到满足堆的性质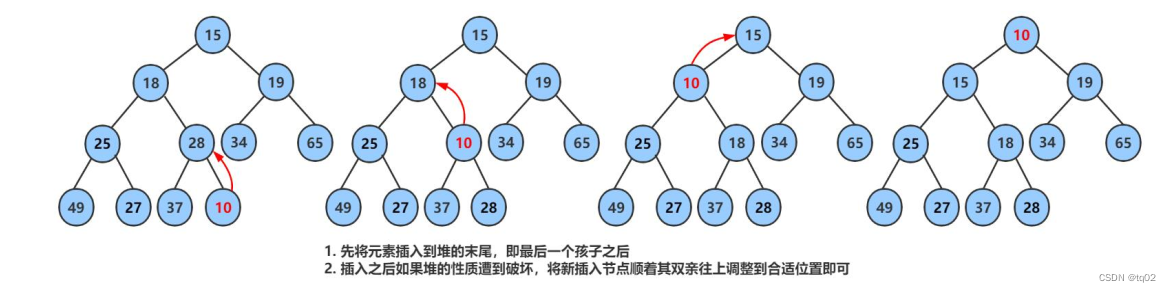 代码实现:
代码实现:
//该方法是传递已经添加了新元素的数组,以及末尾元素下标
public void shiftUp(int[]array,int child) {
// 找到child的双亲
int parent = (child - 1) / 2;
while (child > 0) {
// 如果双亲比孩子大,parent满足堆的性质,调整结束
if (array[parent] > array[child]) {
break;
}
else{
// 将双亲与孩子节点进行交换
int t = array[parent];
array[parent] = array[child];
array[child] = t;
// 小的元素向下移动,可能到值子树不满足对的性质,因此需要继续向上调增
child = parent;
parent = (child - 1) / 1;
}
}
}堆的删除
删除的是堆顶元素,将堆顶元素与最后一位交换,将堆中有效数据个数减少一位,再进行向下调整。
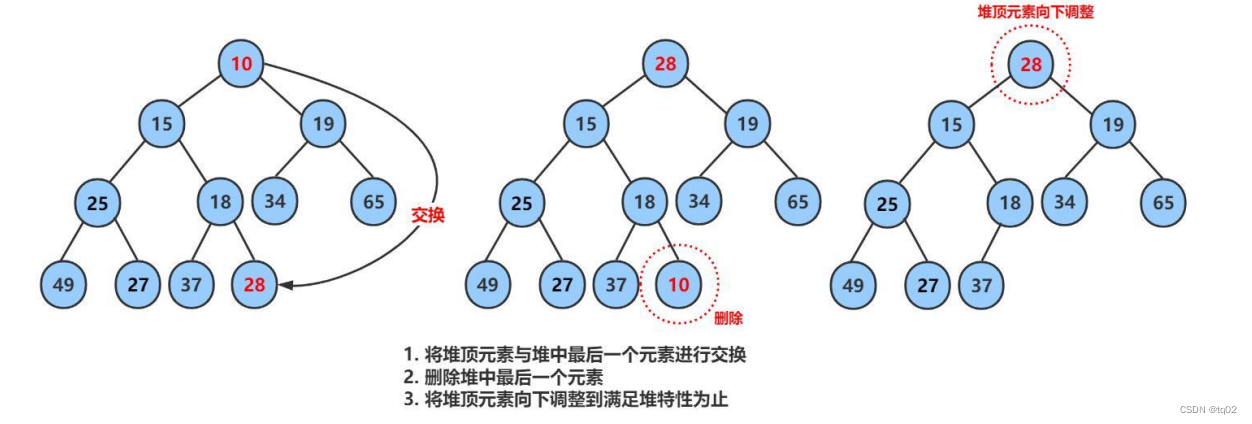
代码实现:
public void delectHeap(MyHeap t)
{
int[] array1=t.array;
int i=array1.length-1;
//swap方法,是交换数组元素
swap(array1,i,0);
//删除末尾元素
array1[index]=0;
t.index--;
//堆顶元素再向下调整
shiftDown(array1,0);
}
二、PriorityQueue
2.1概念
1、 PriorityQueue的类型是优先级队列,优先队列的作用是保证每次取出的元素都是队列中权值最小/最大的
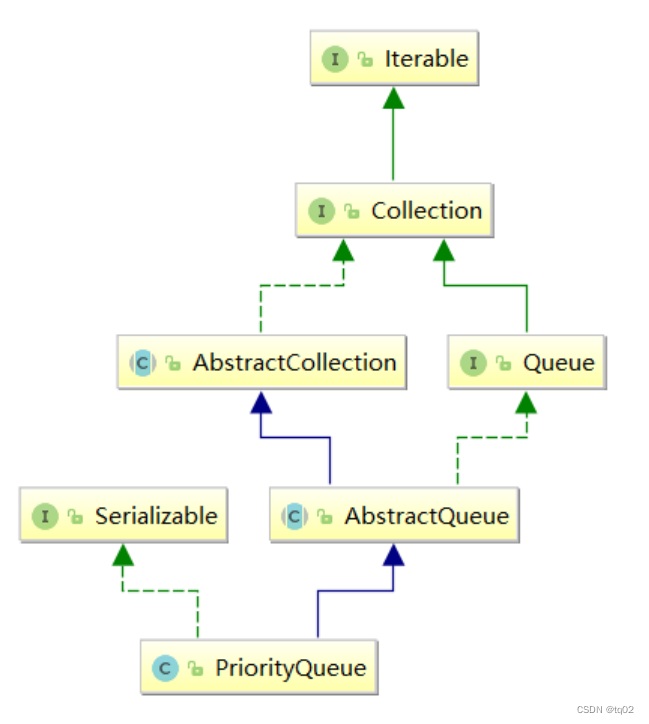
2、 PriorityQueue 是采用 树形结构 来描述元素的存储,具体说是通过完全二叉树实现一个小顶堆,在物理存储方面,PriorityQueue 底层通过 数组 来实现元素的存储。
在集合框架中的联系:
2.2性质
1、底层运用了 堆 数据结构,并且默认情况下,为小堆。
2、默认情况下容量为11,无容量限制,内部可自动扩容。
3、不可以插入无法比较的对象,会抛出异常。
4、不可以插入null对象。
注:因为默认情况为小堆,所以需要大堆时,需要用户提供比较器。
2.3PriorityQueue的创建构造
三种构造方法:
构造器 PriorityQueue() 创建一个空的优先级队列,默认容量:11 PriorityQueue( int capacity) 创建一个初始容量为capacity的优先级队列 PriorityQueue(Collection<? extends E> c) 用一个集合创建优先级队列
代码实例:
public void TestPriorityQueue(){
// 创建一个空的优先级队列,底层默认容量是11
PriorityQueue<Integer> q1 = new PriorityQueue<>();
// 创建一个空的优先级队列,底层的容量为initialCapacity
PriorityQueue<Integer> q2 = new PriorityQueue<>(100);
// 用ArrayList对象来构造一个优先级队列的对象
// q3中已经包含了三个元素
ArrayList<Integer> list = new ArrayList<>();
list.add(4);
list.add(3);
list.add(2);
list.add(1);
PriorityQueue<Integer> q3 = new PriorityQueue<>(list);
System.out.println(q3.size());
System.out.println(q3.peek());
2.4PriorityQueue的操作方法
常用的方法:插入、删除、获取优先级最高(堆顶元素)
函数名 功能介绍 boolean offer(E e) 插入元素e,插入成功返回true,如果e对象为空,抛出NullPointerException异常,时间复杂度 ,注意:空间不够时候会自主扩容 E peek() 获取优先级最高(堆顶)的元素,如果为空,返回null E pool() 移除优先级最高的元素并返回,如果为空,返回null。 int size() 获取有效元素个数 void clear() 清空 Boolean isEmpty() 检测堆是否为空,空返回true 注:如果容量小于64,按照原来的空间*2扩容
如果容量等于64,则按照原来空间*1.5扩容
如果容量超过MAX_ARRAY_SIZE,按照MAX_ARRAY_SIZE来扩容(不需要深究)
代码实现:
public void TestPriorityQueue2(){
int[] arr = {4,1,9,2,8,0,7,3,6,5};
// 一般在创建优先级队列对象时,如果知道元素个数,建议就直接将底层容量给好
// 否则在插入时需要不多的扩容
// 扩容机制:开辟更大的空间,拷贝元素,这样效率会比较低
PriorityQueue<Integer> q = new PriorityQueue<>(arr.length);
for (int e: arr) {
q.offer(e);
}
System.out.println(q.size()); // 打印优先级队列中有效元素个数
System.out.println(q.peek()); // 获取优先级最高的元素
// 从优先级队列中删除两个元素之和,再次获取优先级最高的元素
q.poll();
q.poll();
System.out.println(q.size()); // 打印优先级队列中有效元素个数
System.out.println(q.peek()); // 获取优先级最高的元素
q.offer(0);
System.out.println(q.peek()); // 获取优先级最高的元素
// 将优先级队列中的有效元素删除掉,检测其是否为空
q.clear();
if(q.isEmpty()){
System.out.println("优先级队列已经为空!!!");
}
else{
System.out.println("优先级队列不为空");
}
}总结
我们先得明白堆是什么?堆是一种优先级队列,可采用二叉树的形式来表达存储方式。在Java程序中,以及写好相关的类(PriorityQueue),可以使用。
值得一提的是:Java的集合框架中提供了2种类型的优先级队列:PriorityQueue和PriorityBlockingQueue。但由于PriorityQueue是线程不安全的,PriorityBlockingQueue是线程安全的。