Problem - B - Codeforces

思路：

显然难以讨论<的情况，正难则反，我们尝试计算>的情况
以为每次+a，他的实际贡献给b的是a%m，x也一样，所以他们先取mod
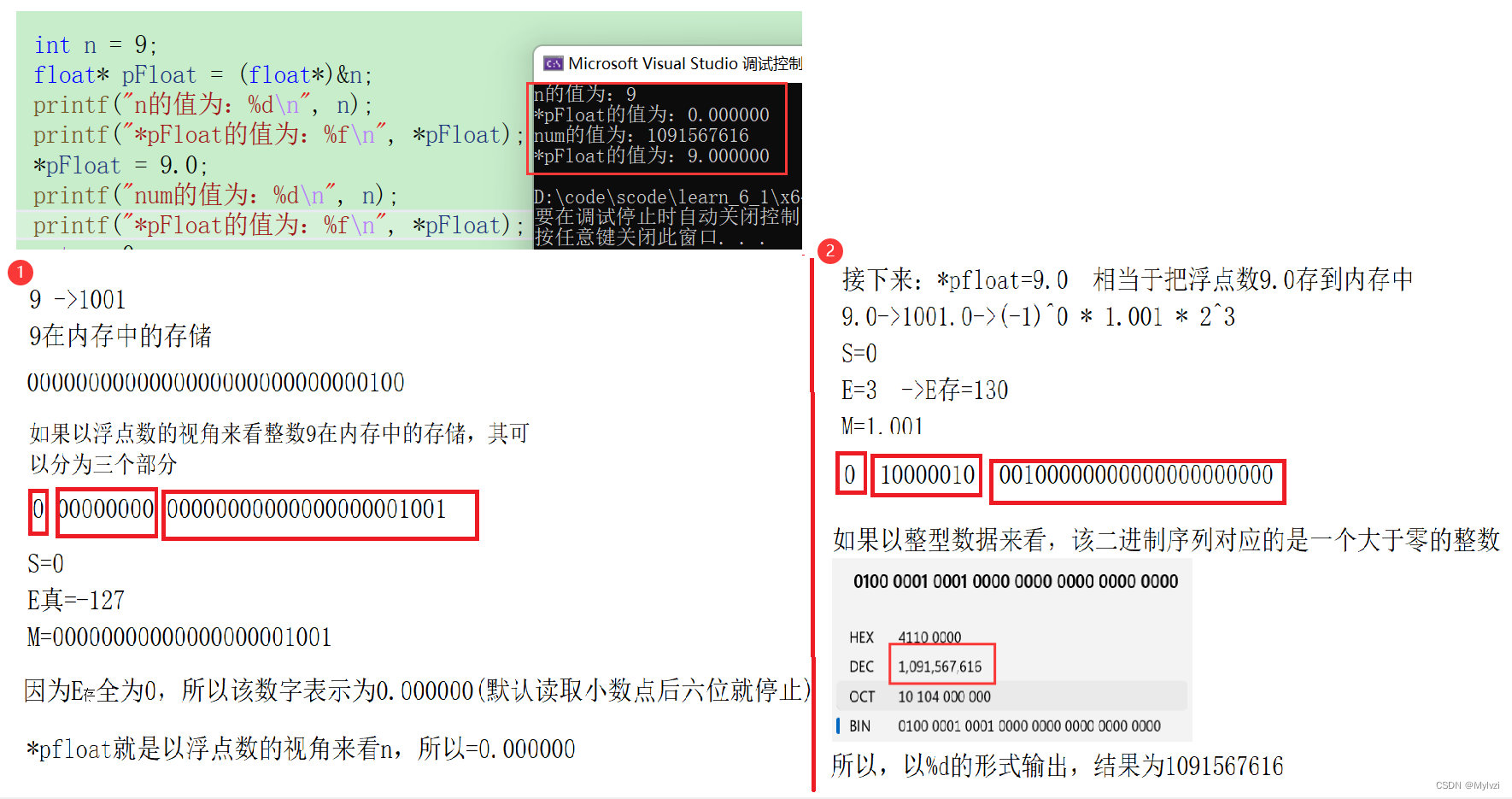
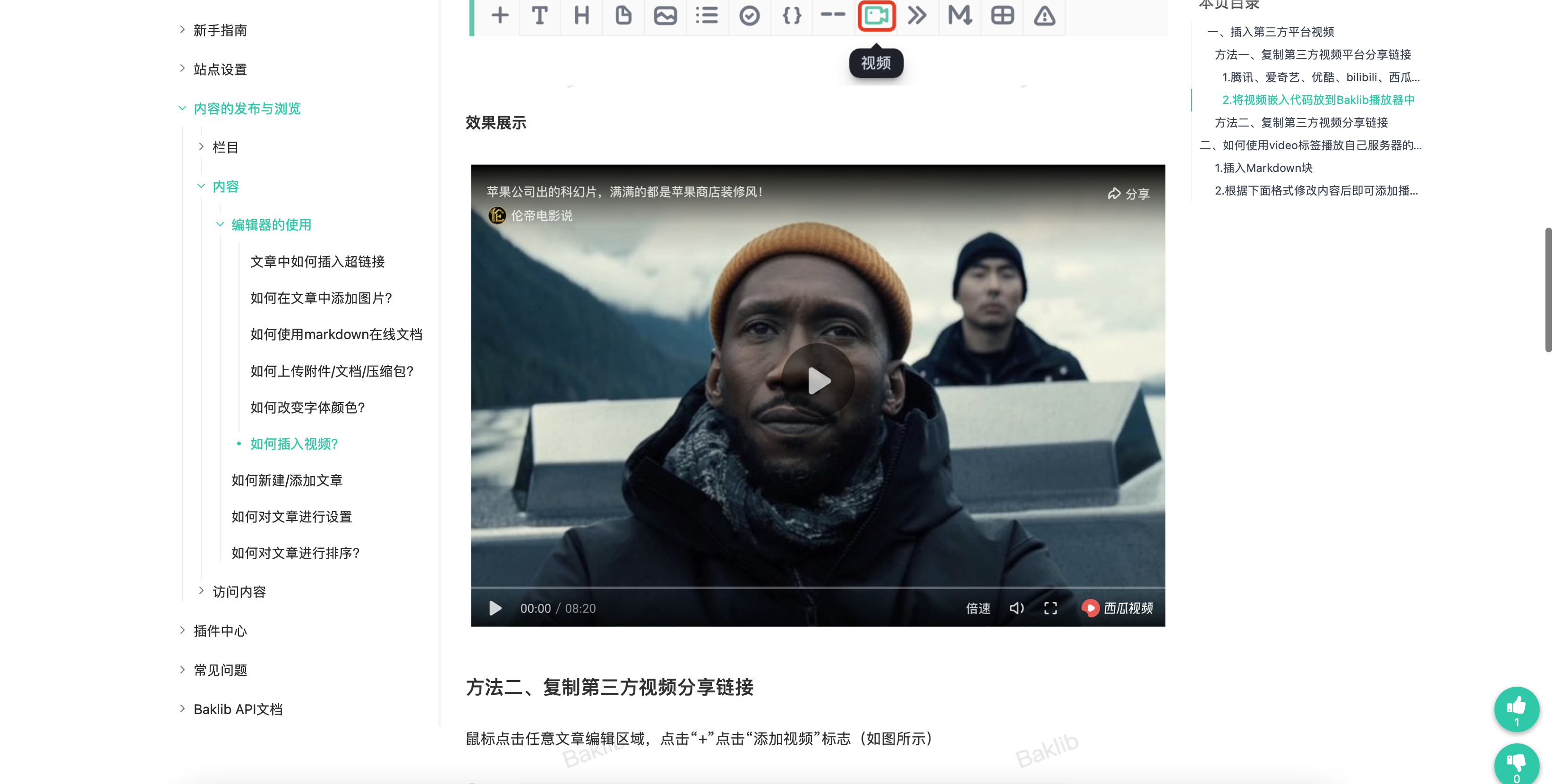
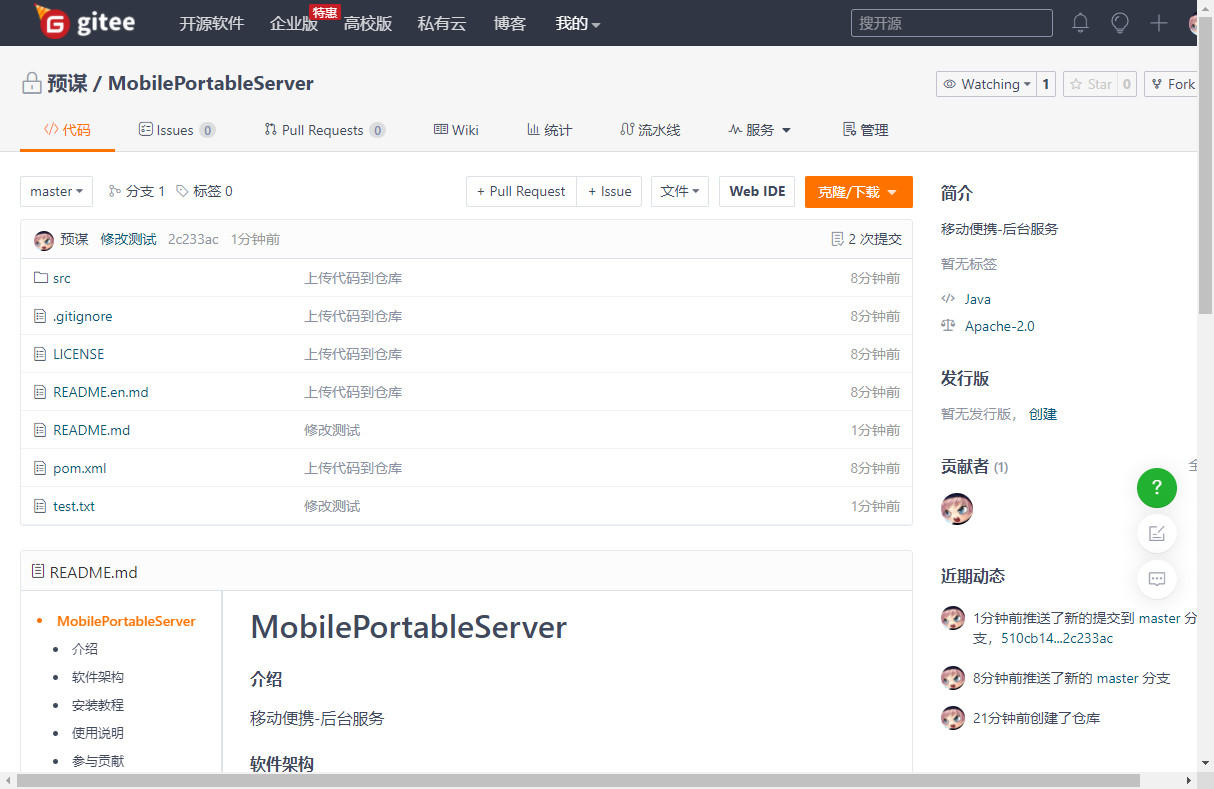
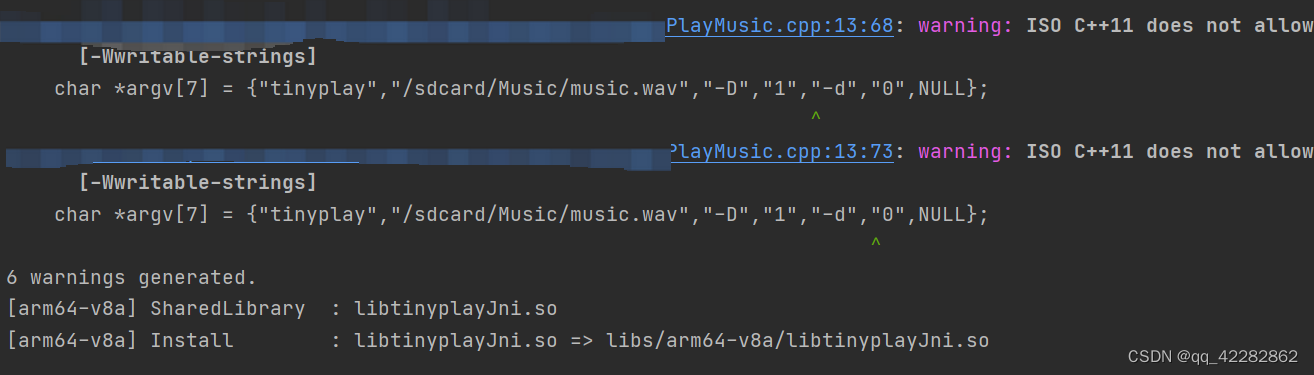
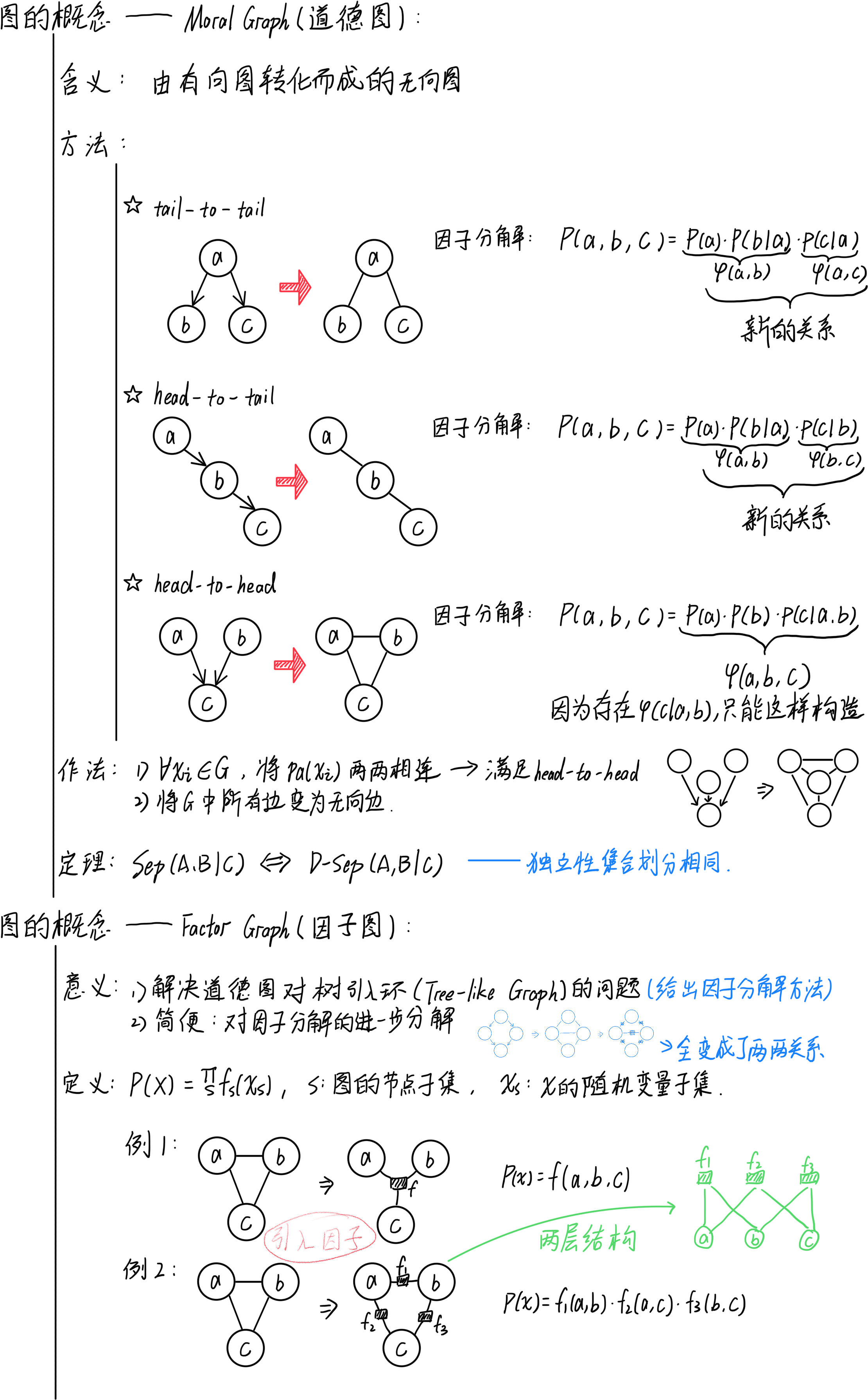
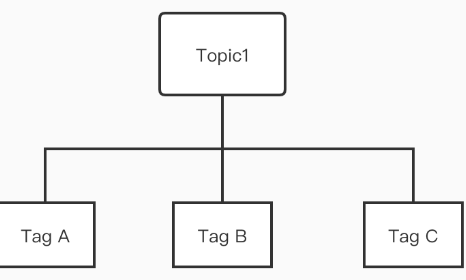
$b[i]>b[i+1]\Leftrightarrow sum>sum+a[i](mod \ m)$ 我们能够大于成立，要求a[i]+sum>mod,换句话说，取模好讨厌，看成除法就是 $\frac{sum}{mod}=\frac{sum+a[i]}{mod}-1$ ，发现所有情况的不等式满足 $\frac{sum}{mod}<=\frac{sum+a[i]}{mod}<=\frac{sum}{mod}+1 \Leftrightarrow \Leftrightarrow \frac{b[i]}{mod}<=\frac{b[i+1]}{mod}<=\frac{b[i]}{mod}+1\Leftrightarrow \Leftrightarrow \frac{b[0]}{mod}<=\frac{b[1]}{mod}<=\frac{b[2]}{mod}<=....<=\frac{b[n]}{mod}$
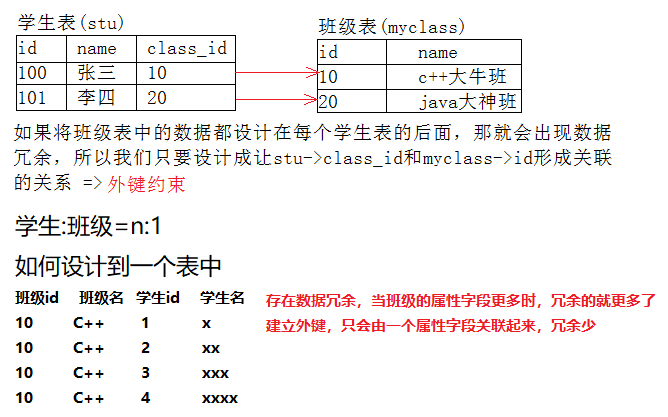
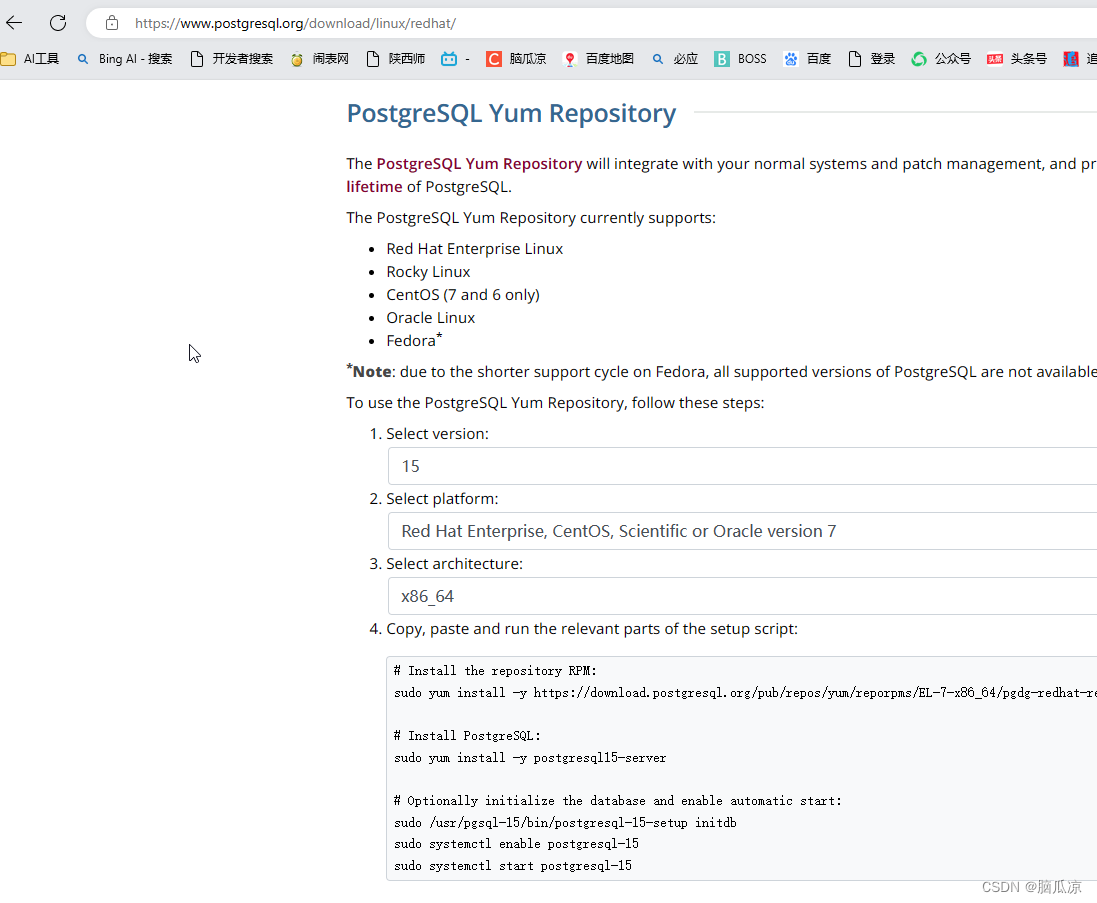
又因为相邻两项差距<=1，所以>的方案数就是 $\frac{b[n]}{mod}$ ，那么答案就是 $n-\frac{b[n]}{mod}$
a与x都要注意取模才去贡献给b

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define endl             "\n"
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define eps 1e-9
#define int              long long
typedef pair<int, int> pii;
inline int read(int &x);
//double 型memset最大127，最小128
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
const int N = 1e6 + 10;
int mod = 998244353;
int sum[N],a[N];
void mysolve()
{
	int k,n,x;
	cin>>k;
	for(int i=1; i<=k; ++i)cin>>a[i];
	cin>>n>>mod>>x;
	for(int i=1; i<=k; ++i)sum[i]=(sum[i-1]+a[i]%mod);
	int end=(x%mod+n/k*sum[k]+sum[n%k])/mod;
	cout<<n-end<<endl;
}

int32_t main()
{
	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);//使用read请把解绑注释了
	int t=1;
	//cin >> t;
	//read(t);
	while (t--)
		{
			mysolve();
		}
	system("pause");
	return 0;
}

Problem - D - Codeforces

思路：

如果dp转移维护的是恰好为k次连续pop的方案数，显然很容易重复。
那如果我维护的是连续pop次数<k，显然可以转移。
1. 我们用dp[i][j]表示处理了i个数，当前还有j个数没有pop出去。我们在转移时也就是i<-i+1，我们是在前i个处理成dp[i][j]的状态后先push进一个i+1，显然他隔断了前面的连续pop，那么我们讨论dp[i+1]的连续pop，就是在i+1push之后，pop出去的<k个。
2. 即dp[i+1][j]可以由dp[i][j-1]+dp[i][j]+..dp[i][j+k-2]得到。（原来有p个未pop，放入i+1后有p+1个未pop，变成j个未pop需要把多余的p+1-j个pop掉)
3. 记录dp前缀和即可
那么答案就是卡特兰数-dp[n][0]

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define endl             "\n"
#define inf 0x3f3f3f3f
#define INF 0x3f3f3f3f3f3f3f3f
#define eps 1e-9
#define int              long long
typedef pair<int, int> pii;
inline int read(int &x);
//double 型memset最大127，最小128
//---------------------------------------------------------------------------------------------------------------------//
//---------------------------------------------------------------------------------------------------------------------//
const int N = 3e3 + 10;
const int mod = 998244353;

int dp[N][N],sum[N][N];
ll pre[N<<2],inv[N<<2];

ll fastmi(ll base, ll power)
{
	ll ans = 1;
	while (power)
		{
			if (power & 1)ans=ans*base%mod;
			base=base*base%mod;
			power >>=1;
		}
	return ans;
}

void mysolve()
{
	int n,k;
	cin>>n>>k;
	if(k==1)
		{
			cout<<pre[2*n]*inv[n]%mod*inv[n]%mod*fastmi(n+1,mod-2)%mod<<endl;
		}
	else
		{
			dp[1][0]=dp[1][1]=1;
			sum[1][0]=1,sum[1][1]=2;
			for(int i=2; i<=n; ++i)
				{
					for(int j=0; j<=i; ++j)
						{
							int l=max(0ll,j-1),r=min(i-1,j+k-2);//dp[i][j]可以由i-1更新的范围
							dp[i][j]=(sum[i-1][r]-(l?sum[i-1][l-1]:0)+mod)%mod;
							sum[i][j]=(dp[i][j]+(j?sum[i][j-1]:0))%mod;
						}
				}
			ll ans=(pre[2*n]*inv[n]%mod*inv[n]%mod*fastmi(n+1,mod-2)%mod-dp[n][0]+mod)%mod;
			cout<<ans<<endl;
		}
}

int32_t main()
{
	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);//使用read请把解绑注释了
	int t=1;
	//cin >> t;
	//read(t);
	pre[0]=1;
	for(int i=1; i<=N<<1; ++i)pre[i]=pre[i-1]*i%mod;
	inv[N<<1]=fastmi(pre[N<<1],mod-2);
	for(int i=(N<<1)-1; ~i; --i)inv[i]=inv[i+1]*(i+1)%mod;
	while (t--)
		{
			mysolve();
		}
	system("pause");
	return 0;
}

Problem - G - Codeforces

思路：

设dp[i]表示处理到i的最小步骤，显然更新dp[i]，我们需要枚举处理到j，复制前缀长度j（下标从0开始），一直粘贴到i需要的最小步骤 $dp[i]=\min_{j=1}^{i-1}( dp[j-1]+1+i-(j-1)-cnt_{j\rightarrow i}*(j-1) )$
$cnt_{j\rightarrow i}$ 表示前缀j在0~i中能够不重叠的出现多少次（不包括开头这个前缀j）。公式理解为处理出前缀j需要的最小次数dp[j-1],复制操作+1，如果无脑从（j-1）一直加一到i，需要i-(j-1)次，如果存在cnt[j],每一个可以减少操作数j-1次
显然我们还有dp[i]<=dp[i-1]+1。
问题是如何处理好到i时所有这个cntj的大小，以及如何使用少于O(n)的时间求出上述公式的所有j中最小值。
1. 观察上述公式，如果把+i提出来，发现如果cntj已经处理出来，显然那一串就是已知值，那么维护区间最小可以线段树优化dp解决。
2. 如何处理cnt呢？
  1. 我们前缀至多有n/2个，长度为i的前缀在整个字符串的cnt<=n/i,这些cnt和起来有 $\sum_{i=1}^{n/2}\frac{n}{i}\Leftrightarrow logn$ (调和级数），显然如果我们能够每次i都不重不漏的更新这些cnt，显然只需要处理nlogn次，这是可以接受的。
  2. 而我们设字符串0~i的前缀函数值为p[i]，在i处显然只需要更新前缀长度p[i]，已经p[i]的祖先们(长度p[i]可以存在的所有前缀）,显然如果遍历这些祖先，我们枚举次数是会重复从而退化到 $O(n^{2})$
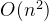
  3. 我们需要解决的是就是能不能处理到i时，在小于O(n)的操作下，询问出p[i]及其说有祖先们需要更新的个数，这样我们就能不重复的更新。发现前缀们其实是一棵以前缀长度0为根节点的树(border树)，如果我们使用树剖维护，显然可以logn查询p[i]及其所有祖先有谁需要更新(即询问p[i]这个节点到0根节点的路径上有谁需要更新)
  4. 接下来转化成的问题就是怎么知道路径上那些点需要更新呢，显然我们可以记录每个前缀上次更新cntj时尾部的下标lastj，如果lastj+j<=i，显然可以cntj++。
  5. 明显的，初始cnt为0时，last就是前缀长度(防止与初始这个前缀重叠)
  6. 因此，解决此问题，只需要树剖维护每个前缀的last+j的最小值还有区间val最小值。（val就是 $( dp[j-1]+1-(j-1)-cnt_{j\rightarrow i}*(j-1) )$ （少了个i）
  7. 更新到i，先查询出需要更新的前缀(即那些lastj+j<=i的点)进行更新。最后dp[i]=i+min[val]

#include <bits/stdc++.h>
using namespace std;
#define ll               long long
#define inf 0x3f3f3f
const int N = 1e5 + 10;

struct node
{
	int next, to;
} edge[N << 1];

int num, cnt;
int head[N << 1], sz[N], dep[N], fa[N], son[N], top[N], idx[N];
int dp[N];
void add(int u, int v)
{
	edge[++num].next = head[u];
	edge[num].to = v;
	head[u] = num;
}

//---------以下是线段树代码-------//
#define ls p<<1
#define rs p<<1|1
#define mid  (t[p].l + ((t[p].r - t[p].l) >> 1))

struct tree
{
	int l, r;
	ll val;//维护最大值
	int cnt,last,dot;//dot为前缀长度
	int len;//len为last+dot,维护最小值
} t[N<<2];

bool vis[N];
int a[N];

void pushup(int p)
{
	t[p].val=min(t[ls].val,t[rs].val);
	if(t[ls].len<t[rs].len)t[p].dot=t[ls].dot,t[p].len=t[ls].len;
	else if(t[ls].len==t[rs].len)t[p].len=t[ls].len,t[p].dot=min(t[ls].dot,t[rs].dot);
	else t[p].dot=t[rs].dot,t[p].len=t[rs].len;
}

void build(int l, int r, int p)
{
	t[p].l = l, t[p].r = r;
	t[p].val=inf,t[p].cnt=0;//初始化
	if (l == r)
		{
			t[p].dot=a[l];
			t[p].last=a[l]-1;

			if(t[p].dot==0)t[p].last=inf;
			t[p].len=t[p].last+a[l];
			return;
		}
	build(l, mid, ls),build(mid + 1, r, rs);
	pushup(p);
}

void update(int l, int r, int p, int w)
{
	if (l <= t[p].l && t[p].r <= r&&t[p].r==t[p].l)
		{
			t[p].last=w,t[p].cnt++;
			t[p].len=t[p].last+t[p].dot;
			t[p].val=dp[a[l]-1]+1-(a[l]-1)-t[p].cnt*(a[l]-1);
			return;
		}
	if (l <= mid)update(l, r, ls, w);
	if (r > mid)update(l, r,rs, w);
	pushup(p);
}

int ask(int l, int r, int p)
{
	if (l <= t[p].l && t[p].r <= r)return t[p].val;
	int ans = inf;
	if (l <= mid)ans=min(ans,ask(l,r,ls));
	if (r > mid)ans =min(ans, ask(l,r,rs));
	return ans;
}

int askpoint(int l,int r,int p,int w)
{
	if (l <= t[p].l && t[p].r <= r)
		{
			if(t[p].len<=w)return t[p].dot;
			else return 0;
		}
	if (l <= mid)
		{
			int tmp=askpoint(l,r,ls,w);
			if(tmp)return tmp;
		}
	if(r>mid)
		{
			int tmp=askpoint(l,r,rs,w);
			if(tmp)return tmp;
		}
	return 0;
}

//------以上是线段树代码------//

void dfs1(int u, int f)//建树
{
	fa[u] = f;
	vis[u]=1;
	dep[u] = dep[f] + 1;
	sz[u] = 1, son[u] = idx[u] = 0;//初始化
	int mx = -1;
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (v == f||vis[v])continue;
			dfs1(v, u);
			sz[u] =(sz[u]+sz[v]);
			if (sz[v] > mx)mx = sz[v], son[u] = v;//更新重儿子
		}
}

void dfs2(int u, int topfa)
{
	top[u] = topfa;//记录链顶点
	idx[u] = ++cnt;
	a[cnt] =u;
	if (!son[u])return;//没儿子
	dfs2(son[u], topfa);//重儿子优先编号
	for (int i = head[u]; i; i = edge[i].next)
		{
			int v = edge[i].to;
			if (!idx[v])dfs2(v, v);//v是自己轻链的顶点
		}
}

void treeadd(int x, int y, int w)
{
	update(idx[x], idx[y], 1, w);
}

int treeask(int x, int y)//询问最小val
{
	int ans = inf;
	while (top[x] != top[y])
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);
			ans = min(ans, ask(idx[top[x]], idx[x], 1));
			x = fa[top[x]];
		}
	if (dep[x] > dep[y])swap(x, y);
	ans = min(ans, ask(idx[x], idx[y], 1));
	return ans;
}

int  treeaskpoint(int x, int y,int w)//询问是否存在需要更新的点
{
	while (top[x] != top[y])
		{
			if (dep[top[x]] < dep[top[y]])swap(x, y);
			int tmp= askpoint(idx[top[x]], idx[x], 1,w);
			if(tmp!=0)return tmp;
			x = fa[top[x]];
		}
	if (dep[x] > dep[y])swap(x, y);
	int tmp= askpoint(idx[x], idx[y], 1,w);
	return tmp;
}

int p[N];
void mysolve()
{
	string s;
	cin >> s;
	int n=(int)s.size();
	p[0] = 0;//只有一个字符，当然为0
	for (int i = 1; i < n; ++i)//从2个字符以上开始（i=1开始）
		{
			int j = p[i - 1];//每次都先取上一次i-1长度的最长前缀长度，接下来判断是否s[i]==s[j],因为下标从0开始，j是长度，所以j刚好就是最长前缀的下一位，如果判断两者相同，不用走while，直接j+1
			while (j  && s[i] != s[j])j = p[j-1];//如果不相等，范围缩小为p[j-1],j-1是比原来前缀少1，p[j-1]就是在这个前缀范围找前缀，如果为0，就是没有前缀，所以为0跳出（用j>0限制）
			if (s[i] == s[j])++j;//如果出来（没进去while也一样）相等，说明下一位相同，j+1
			p[i] = j;//存储p[i+1]
			if(p[i])add(p[p[i]-1],p[i]);
		}
	dep[0]=-1;
	cnt=0;
	dfs1(0, 0);//建树
	dfs2(0, 0);//从根节点开始重新编号
	build(1,cnt, 1);
	dp[0]=1;
	for(int i=1; i<n; ++i)
		{
			dp[i]=dp[i-1]+1;
			while(1)//询问需要更新的点，这个操作最多执行nlogn次
				{
					int tmp=0;
					if(p[i])tmp=treeaskpoint(0,p[i],i);
					if(tmp)treeadd(tmp,tmp,i);
					else break;
				}
			if(p[i]>0)dp[i]=min(dp[i],i+treeask(0,p[i]));
		}
	cout<<dp[n-1]<<endl;
}

int32_t main()
{
	mysolve();
	system("pause");
	return 0;
}

Problem - H - Codeforces

思路：

不难观察出a[i]在找到右边第一个大于a[i]的数之前，中间那些数必须与a[i]放在一个字符串才行。我们把a[i]到右边第一个比他大的数中间那些数与a[i]绑在一起
所以我们可以使用单调栈处理，最后变成处理后的这堆数，能不能凑出n/2这个数——>背包问题
但是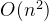必定被t啊（~~虽然我vp时强行n^2优化ac了~~）。
1. 但是观察到这些数和为n，求的是n/2，本质这些数实际最多只有 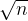$\sqrt{n}$ 个 $(1+2+3+....+ \sqrt{n})=n^{2}$ ，所以我们把相同的数凑一起，等于跑个多重背包（再用二进制优化一下)就跑得很快，可以 $O(n\sqrt{n})$ 解决。

#include<bits/stdc++.h>
#define ll long long
#define endl '\n'
using namespace std;
const int N=5e5+5;
typedef pair<int,int> pii;

int a[N],mn[N];
void mysolve()
{
	int n;
	cin>>n;
	for(int i=1; i<=n; ++i)cin>>a[i],mn[i]=0;
	stack<pii>s;
	s.push({a[1],1});
	for(int i=2; i<=n; ++i)
		{
			if(!s.empty())
				{
					while(!s.empty()&&s.top().first<a[i])
						{
							pii u=s.top();
							s.pop();
							mn[u.second]=i;
						}
				}
			s.push({a[i],i});
		}
	unordered_map<int,int>mp;
	for(int i=1; i<=n; ++i)
		{
			if(mn[i])
				{
					mp[mn[i]-i]++;
					i=mn[i]-1;
				}
			else
				{
					mp[n-i+1]++;
					break;
				}
		}
	vector<int>v;
	for(pii u:mp)//二进制背包
		{
			int cnt=u.second;
			int t=1;
			while(t<=cnt)
				{
					v.push_back(u.first*t);
					cnt-=t,t<<=1;
				}
			if(cnt)v.push_back(u.first*cnt);
		}
	bitset<N/2>dp;
	dp.reset();
	dp.set(0);
	for(auto k:v)
		{
			dp=dp|(dp<<k);
			if(dp[n/2])
				{
					cout<<"Yes"<<endl;
					return;
				}
		}
	cout<<"No"<<endl;
}

signed main()
{
	std::ios::sync_with_stdio(0), cin.tie(0), cout.tie(0);//使用read请把解绑注释了
	int t;
	cin>>t;
	while(t--)
		{
			mysolve();
		}
}