Additive Models

to avoid the curse of dimensionality and for better interpretability we assume
$$m(\mathbf{x})=E(Y|\mathbf{X}=\mathbf{x})=c+\sum _{j=1}^d{g}_j(x_j)$$
$⟹$ the additive functions $g_j$ can be estimated with the optimal one-dimensional rate

two possible methods for estimating an additive model:

• backfitting estimator
• marginal integration estimator
  indentification conditions for both methods

E X j { g ( X j ) } = 0 , ∀ j = 1 , … , d ⟹ E ( Y ) = e \begin{aligned} E_{X_j}\{ g(X&_j) \}=0, \forall j=1,\dots,d\\ & \Longrightarrow E(Y)=e \end{aligned} EXj​​{g(X​j​)}=0,∀j=1,…,d⟹E(Y)=e​

formulation Hibert space framework:

• let ${\mathcal{H}}_{Y\mathbf{X}}$ be the Hilbert space of random variables which are functions of $Y,\mathbf{X}$
• let $⟨U,V⟩=E(UV)$ the scalar product
• define ${\mathcal{H}}_{\mathbf{X}}$ and ${\mathcal{H}}_X,j=1,\dots ,d$ the corresponding subspaces

$⟹$ we aim to find the element of ${\mathcal{H}}_{X_1}\oplus \cdots \oplus {\mathcal{H}}_{X_d}$ closest to $Y\in {\mathcal{H}}_{Y\mathbf{X}}$ or $m\in {\mathcal{H}}_{\mathbf{X}}$
by the projection theorem, there exists a unique solution with
E [ { Y − m ( X ) } ∣ X α ] = 0    ⟺    g α ( X α ) = E [ { Y − ∑ j ≠ α g j ( X j ) } ∣ X α ] , α = 1 , … , d E[\{ Y-m(\boldsymbol{X}) \}|X_{\alpha}]=0\\ \iff g_{\alpha}(X_{\alpha})=E[\{ Y-\sum_{j\neq\alpha}g_j(X_j) \}|X_{\alpha}], \quad\alpha=1,\dots,d E[{Y−m(X)}∣Xα​]=0⟺gα​(Xα​)=E[{Y−j=α∑​gj​(Xj​)}∣Xα​],α=1,…,d
denote projection $P_{\alpha }(\bullet )=E(\bullet |X_{\alpha })$
$$⟹\left(\begin{array}{cccc}I& P_1& \cdots & P_1\\ P_2& I& \cdots & P_2\\ ⋮& & \ddots & ⋮\\ P_d& \cdots & P_d& I\end{array}\right)\left(\begin{array}{c}{g}_1\left(X_1\right)\\ g_2\left(X_2\right)\\ ⋮\\ g_d\left(X_d\right)\end{array}\right)=\left(\begin{array}{c}{P}_{1}Y\\ P_{2}Y\\ ⋮\\ P_{d}Y\end{array}\right)$$
denote by
$${\mathbf{S}}_{\alpha }\text{the}(n\times n)\text{smoother matrix}$$
such that ${\mathbf{S}}_{\alpha }\mathbf{Y}$ is an estimate of the vector { E ( Y 1 ∣ X α 1 ) , … , E ( Y n ∣ X α n ) } ⊤ \{ E(Y_1|X_{\alpha1}),\dots,E(Y_n|X_{\alpha n}) \}^{\top} {E(Y1​∣Xα1​),…,E(Yn​∣Xαn​)}⊤
$$⟹\underset{nd\times nd}{\underbrace{\left(\begin{array}{cccc}\mathbf{I}& {\mathbf{S}}_1& \cdots & {\mathbf{S}}_1\\ {\mathbf{S}}_2& \mathbf{I}& \cdots & {\mathbf{S}}_2\\ ⋮& & \ddots & ⋮\\ {\mathbf{S}}_d& \cdots & {\mathbf{S}}_d& \mathbf{I}\end{array}\right)}}\left(\begin{array}{c}{\mathbf{g}}_1\\ {\mathbf{g}}_2\\ ⋮\\ {\mathbf{g}}_d\end{array}\right)=\left(\begin{array}{c}{\mathbf{S}}_1\mathbf{Y}\\ {\mathbf{S}}_2\mathbf{Y}\\ ⋮\\ {\mathbf{S}}_d\mathbf{Y}\end{array}\right)$$
note: infinite samples the matrix on the left side can be singular

Bacfitting algorithm

in practice, the following backfitting algorithm (a simplification of the Gauss-Seidel procedure) is used:

---

• initialize ${\hat{\mathbf{g}}}^{(0)}\equiv 0\forall \alpha ,\hat{c}=\bar{Y}$
• repeat for $\alpha =1,\dots ,d$
  $$\begin{array}{rl}{\mathbf{r}}_{\alpha }& =\mathbf{Y}-\hat{c}-\sum _{j=1}^{\alpha -1}{\hat{\mathbf{g}}}_j^{(\ell +1)}-\sum _{j=\alpha +1}^d{\hat{\mathbf{g}}}_j^{(\ell )}\\ {\hat{\mathbf{g}}}_{\alpha }^{(\ell +1)}(\bullet )& ={\mathbf{S}}_{\alpha }\left({\mathbf{r}}_{\alpha }\right)\end{array}$$
• proceed until convergence is reached

---

Example: smoother performance in additive models

simulated sample of $n=75$ regression observations with regressors $X_j$ i.i.d.
uniform on $[-2.5,2.5]$, generated from
$$Y=\sum _{j=1}^4{g}_j(X_j)+\epsilon ,\epsilon \sim N(0,1)$$
where
g 1 ( X 1 ) = − sin ⁡ ( 2 X 1 ) g 2 ( X 2 ) = X 2 2 − E ( X 2 2 ) g 3 ( X 3 ) = X 3 g 4 ( X 4 ) = exp ⁡ ( − X 4 ) − E { exp ⁡ ( − X 4 ) } \begin{array}{ll} g_1\left(X_1\right)=-\sin \left(2 X_1\right) & g_2\left(X_2\right)=X_2^2-E\left(X_2^2\right) \\ g_3\left(X_3\right)=X_3 & g_4\left(X_4\right)=\exp \left(-X_4\right)-E\left\{\exp \left(-X_4\right)\right\} \end{array} g1​(X1​)=−sin(2X1​)g3​(X3​)=X3​​g2​(X2​)=X22​−E(X22​)g4​(X4​)=exp(−X4​)−E{exp(−X4​)}​
Plotting results in this example:

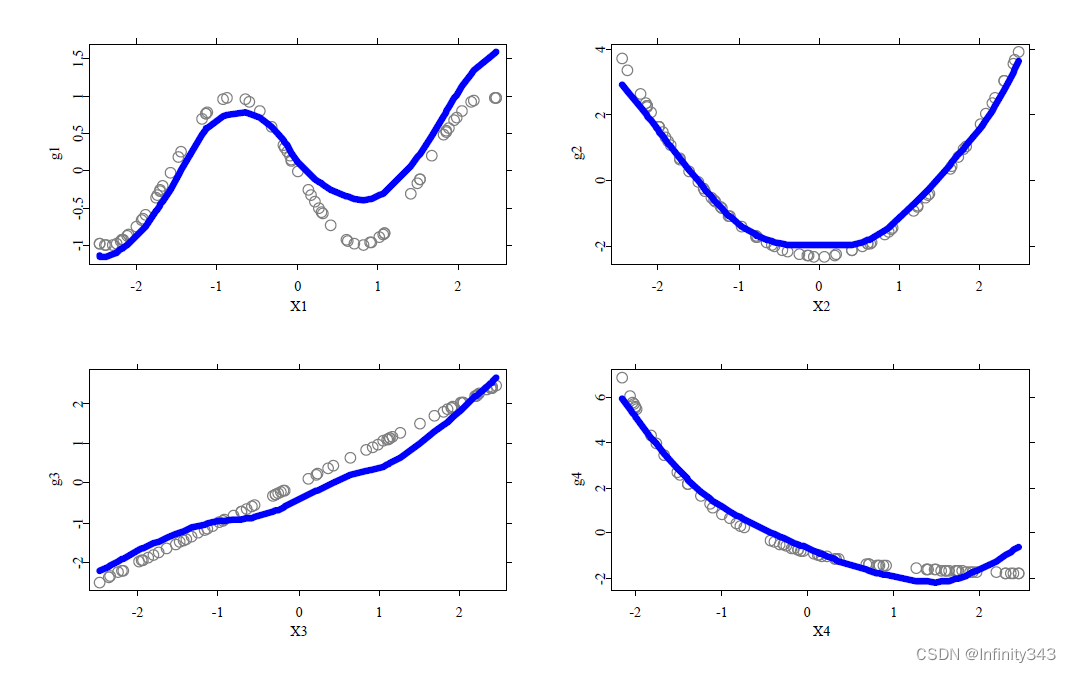
Code:

n = 75
X = matrix(NA, n, 4)
for (i in 1:4) {
  X[, i] = runif(n, min = -2.5, max = 2.5)
}

g1 = function(x) {
  return(-sin(2 * x))
}

g2 = function(x) {
  return(x ^ 2 - mean(x ^ 2))
}

g3 = function(x) {
  return(x)
}

g4 = function(x) {
  return(exp(-x) - mean(exp(-x)))
}
eps = rnorm(n)

###indicator function
I = function(x, index) {
  if (index == 1) {
    return(x)
  }
  if (index == 0) {
    return(0)
  }
}

x <- seq(-2.5, 2.5, l = 100)
Y = I(g1(X[, 1]), 1) + I(g2(X[, 2]), 0) + I(g3(X[, 3]), 0) + I(g4(X[, 4]), 0) + eps
fit_g1 <- loess(
  Y ~ x,
  family = 'symmetric',
  degree = 2,
  span = 0.7,
  data = data.frame(x = X[, 1], Y = Y),
  surface = "direct"
)
out_g1 <- predict(fit_g1,
                  newdata = data.frame(newx = x),
                  se = TRUE)
low_g1 <- out_g1$fit - qnorm(0.975) * out_g1$se.fit
high_g1 <- out_g1$fit + qnorm(0.975) * out_g1$se.fit
df.low_g1 <- data.frame(x = x, y = low_g1)
df.high_g1 <- data.frame(x = x, y = high_g1)
P1 = ggplot(data = data.frame(X1 = X[, 1], g1 = Y),
            aes(X1, g1)) +
  geom_point() +
  geom_smooth(method = "loess", show.legend = TRUE) +
  geom_line(data = df.low_g1, aes(x, y), color = "red") +
  geom_line(data = df.high_g1, aes(x, y), color = "red")

Y = I(g1(X[, 1]), 0) + I(g2(X[, 2]), 1) + I(g3(X[, 3]), 0) + I(g4(X[, 4]), 0) + eps
fit_g2 <- loess(
  Y ~ x,
  family = 'symmetric',
  degree = 2,
  span = 0.9,
  data = data.frame(
    x = X[, 2],
    Y = (Y - fit_g1$fitted),
    surface = "direct"
  )
)
out_g2 <- predict(fit_g2,
                  newdata = data.frame(newx = x),
                  se = TRUE)
low_g2 <- out_g2$fit - qnorm(0.975) * out_g2$se.fit
high_g2 <- out_g2$fit + qnorm(0.975) * out_g2$se.fit
df.low_g2 <- data.frame(x = x, y = low_g2)
df.high_g2 <- data.frame(x = x, y = high_g2)
P2 = ggplot(data = data.frame(X2 = X[, 2], g2 = (Y - fit_g1$fitted)),
            aes(X2, g2)) +
  geom_point() +
  geom_smooth(method = "loess", show.legend = TRUE) +
  geom_line(data = df.low_g2, aes(x, y), color = "red") +
  geom_line(data = df.high_g2, aes(x, y), color = "red")

Y = I(g1(X[, 1]), 0) + I(g2(X[, 2]), 0) + I(g3(X[, 3]), 1) + I(g4(X[, 4]), 0) + eps
fit_g3 <- loess(
  Y ~ x,
  family = 'symmetric',
  degree = 2,
  span = 0.9,
  data = data.frame(
    x = X[, 3],
    Y = (Y - fit_g1$fitted - fit_g2$fitted),
    surface = "direct"
  )
)
out_g3 <- predict(fit_g3,
                  newdata = data.frame(newx = x),
                  se = TRUE)
low_g3 <- out_g3$fit - qnorm(0.975) * out_g3$se.fit
high_g3 <- out_g3$fit + qnorm(0.975) * out_g3$se.fit
df.low_g3 <- data.frame(x = x, y = low_g3)
df.high_g3 <- data.frame(x = x, y = high_g3)
P3 = ggplot(data = data.frame(X3 = X[, 3], g3 = (Y - fit_g1$fitted - fit_g2$fitted)),
            aes(X3, g3)) +
  geom_point() +
  geom_smooth(method = "loess", show.legend = TRUE) +
  geom_line(data = df.low_g3, aes(x, y), color = "red") +
  geom_line(data = df.high_g3, aes(x, y), color = "red")

Y = I(g1(X[, 1]), 0) + I(g2(X[, 2]), 0) + I(g3(X[, 3]), 0) + I(g4(X[, 4]), 1) + eps
fit_g4 <- loess(
  Y ~ x,
  family = 'symmetric',
  degree = 2,
  span = 0.9,
  data = data.frame(
    x = X[, 4],
    Y = (Y - fit_g1$fitted - fit_g2$fitted - fit_g3$fitted),
    surface = "direct"
  )
)
out_g4 <- predict(fit_g4,
                  newdata = data.frame(newx = x),
                  se = TRUE)
low_g4 <- out_g4$fit - qnorm(0.975) * out_g4$se.fit
high_g4 <- out_g4$fit + qnorm(0.975) * out_g4$se.fit
df.low_g4 <- data.frame(x = x, y = low_g4)
df.high_g4 <- data.frame(x = x, y = high_g4)
P4 = ggplot(data = data.frame(
  X4 = X[, 4],
  g4 = (Y - fit_g1$fitted - fit_g2$fitted - fit_g3$fitted)
),
aes(X4, g4)) +
  geom_point() +
  geom_smooth(method = "loess", show.legend = TRUE) +
  geom_line(data = df.low_g4, aes(x, y), color = "red") +
  geom_line(data = df.high_g4, aes(x, y), color = "red")

cowplot::plot_grid(P1, P2, P3, P4, align = "vh")

result:

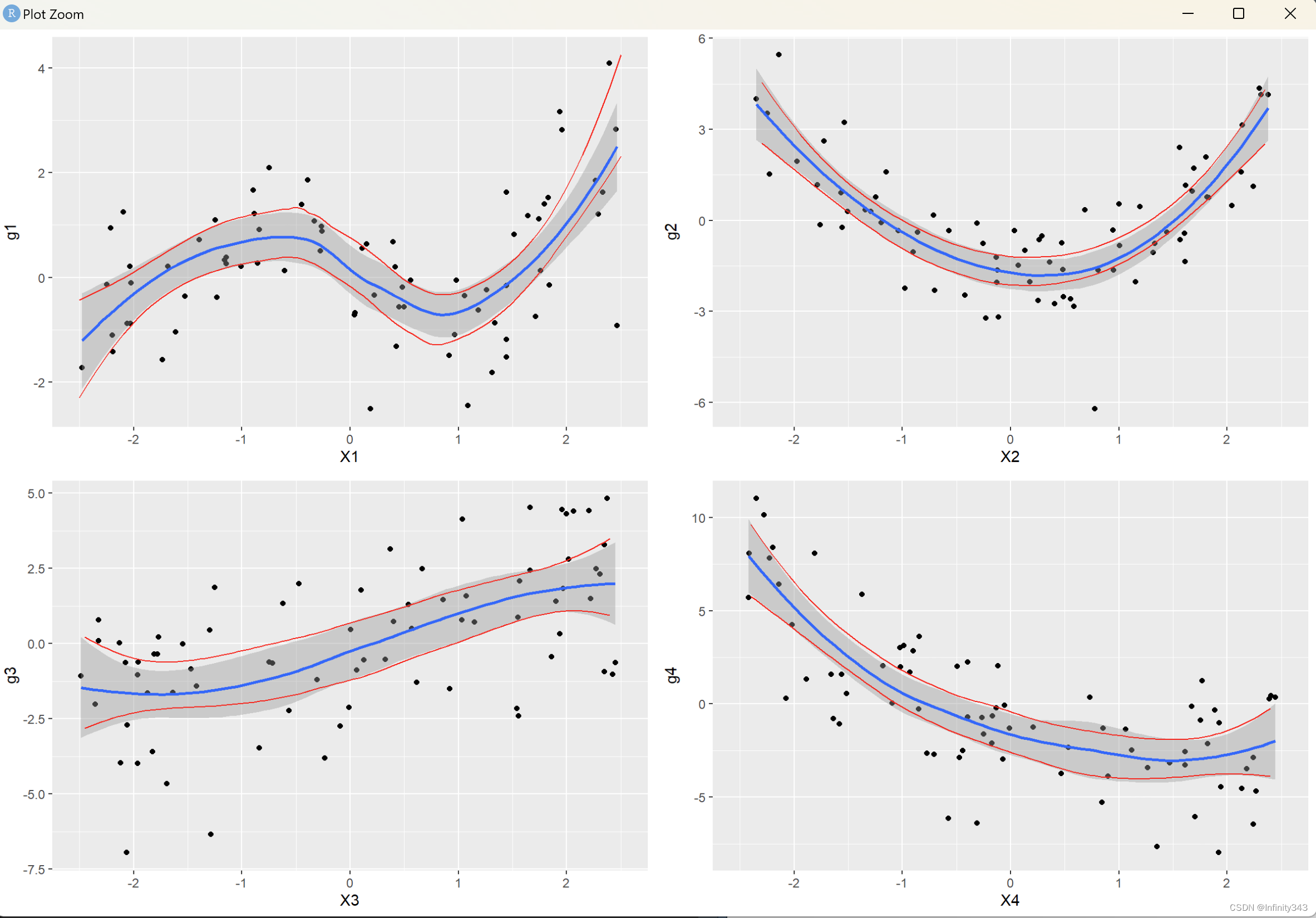
参考文献

https://academic.uprm.edu/wrolke/esma6836/smooth.html

Hastie, T. J. and Tibshirani, R. J. (1990). Generalized Additive Models, Vol. 43 of Monographs on Statistics and Applied Probability, Chapman and Hall, London.

Opsomer, J. and Ruppert, D. (1997). Fitting a bivariate additive model by local polynomial regression, Annals of Statistics 25: 186-211.

Mammen, E., Linton, O. and Nielsen, J. P. (1999). The existence and asymptotic properties of a backfitting projection algorithm under weak conditions, Annals of Statistics 27: 1443-1490.