线性规划中，我们介绍了三种求解算法——单纯形法、对偶理论和内点法。

传送门：线性规划之单纯形法 线性规划的对偶理论 线性规划之内点法

其中单纯形法要建立在标准型上，并且开始迭代要求有一个基本可行解。如果系数矩阵A规模较大，有时候比较难找到初始可行解。这时候需要用人工手段增加变量，来找到初始可行解。具体方法为：

通过从每个约束行中选取系数在对应列向量中唯一非零，而且系数符号与右边项一致的变量作为基变量，可以构造单纯形法的初始基。如果标准型中没有满足条件的变量，可以引入人工变量。此时目标函数为求人工变量之和最小化的问题，即目标函数除人工变量系数为1外，其余变量系数均为0.

我们举一个例子，对于下面的标准型LP问题，引入人工变量找到初始可行集：

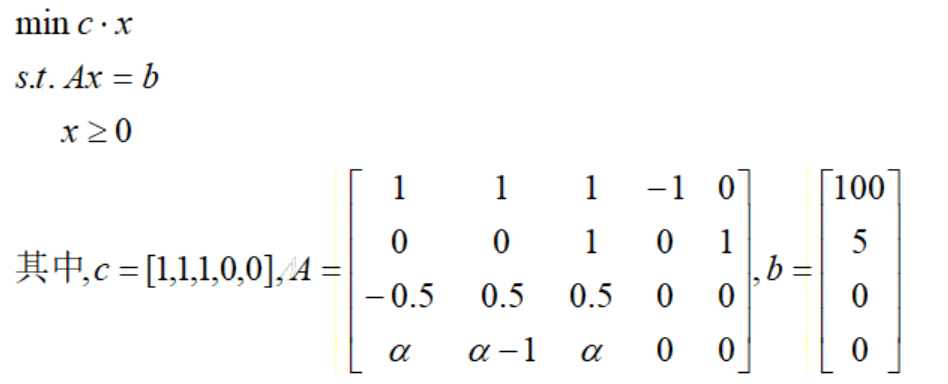
首先看第一个约束，变量x4系数在列向量中唯一非零，但其系数为负，而对应的右边项系数为正，因此需要引入人工变量x6；第二个约束，变量x5系数在列向量中唯一非零，且符号与右边项一致，因此x5可作为初始基。第三第四个约束均没有满足条件的向量，引入人工变量x7和x8。

此时要求解的目标函数变为：

最后四列即可新LP问题的初始可行解，通过单纯形法可以求解最优解。最后还需要检验该问题最优解是否为原模型的可行解。判断标准为：

如果人工变量之和最小值大于0，则原模型无可行解，计算到此为止，否则人工模型最后的基作为求解原模型的初始可行基

我们用python开发完整的单纯形法代码，包含人工模型的（阶段一）以及求解原模型（阶段二）的过程。考虑到有些场景可以直接找到原模型初始可行解，因此阶段一不一定用得上，因此用python的装饰器实现。

import numpy as np
import pandas as pd
from numpy.linalg import det,inv #求解矩阵的秩和逆矩阵


class Simplex(object):
    '''
    单纯形法求解最值问题,这里固化为求最小值，要是遇到求最大值，将目标系数向量取负号即可
    '''


    def __init__(self, A, b, c, B_x):


        '''


        :param A: 系数矩阵
        :param b: 常数向量
        :param c: 目标函数系数向量
        :param B_x: 初始基变量索引列表
        '''
        self.A = A
        self.b = b
        self.c = c
        self.B_x = B_x


    def __call__(self, *args, **kwargs):


        print('单纯形法第二阶段...')
        x = self.phaseII(self.A, self.b, self.c, self.B_x)
        return x


    @classmethod
    def phaseI(cls, manual_n, A_, b, c, B_x_):


        '''
        单纯形法第一阶段，确定初始可行基
        这里人工变量排在矩阵后面
        :param manual_n: 人工变量的个数
        :param A_: 添加人工变量后的系数矩阵
        :param b: 常数向量
        :param c: 目标函数系数向量
        :param B_x_: 初始可行基
        :return:
        '''


        print('单纯形法第一阶段......')
        c_ = [0 for i in range(len(c))] + [1 for i in range(manual_n)]  # 添加人工变量后的目标函数系数向量, 人工变量系数为1，其余均为0
        c_ = np.array(c_)
        x_ = cls.phaseII(A_, b, c_, B_x_)
        a = np.dot(c_, np.array(x_))


        if a > 0:
            print('原模型无可行解')
        else:
            B_x = []
            for n, i in enumerate(x_):
                if i != 0:
                    B_x.append(n)


            return cls(A_[:, :-manual_n], b, c, B_x)


    @staticmethod
    def phaseII(A, b, c, B_x):
        '''


        :param n: 列向量个数
        :param B_x: 初始基变量索引列表
        :return:
        '''


        n = A.shape[1]  # 列向量个数
        N_x = list(filter(lambda x: 0 if x in B_x else 1, [i for i in range(n)]))  # 初始非基变量索引
        init_B = A[:, B_x]  # 基矩阵
        x_0 = np.dot(inv(init_B), b)  # t=0的解
        for i in N_x:
            x_0 = np.insert(x_0, i, 0)


        t, dim = 0, n - len(N_x)
        while True:


            if t >= 100:
                break


            # print('t={}时刻**********'.format(t))
            print('t={}时刻目标函数取值{}:'.format(t, np.dot(c, x_0)))
            # print('入基变量索引：', B_x)
            # print('出基变量索引：', N_x)
            # print('基矩阵：', init_B)
            # print('唯一解：', x_0)


            v = np.dot(c[B_x], inv(init_B))  # 定价向量
            # print('定价向量：', v)
            delta_c = dict(zip([c[i] - np.dot(v, A[:, i]) for i in N_x], N_x))
            # print('非基变量目标函数变化值：', delta_c)


            if min(delta_c) < 0:
                p = delta_c[min(delta_c)]
            else:
                p = -1
                print('计算结束,最优解为：', x_0)
                break


            delta_x = np.dot(-inv(init_B), A[:, p])
            # print('入基变量索引p={}，此时单纯性方向为：{}'.format(p, delta_x))


            if min(delta_x) < 0:
                di = {}
                for i in range(dim):
                    if delta_x[i] < 0:
                        di[B_x[i]] = -x_0[B_x[i]] / delta_x[i]
                lam = min(di.values())
                r = min(di, key=di.get)
            else:
                r = -1
                print('单纯性方向所有元素非负,模型无界')
                break
            # print('出基变量索引r={},此时lamda取值为{}'.format(r,lam))


            E = np.identity(dim)
            E[:, B_x.index(r)] = [
                -1 / delta_x[B_x.index(r)] if i == B_x.index(r) else -delta_x[i] / delta_x[B_x.index(r)]
                for i in range(dim)]
            init_B = inv(np.dot(E, inv(init_B)))


            d = dict(zip(B_x, delta_x))
            delta_x = np.array(list(dict(sorted(d.items(), key=lambda x: x[0])).values()))
            for i in N_x:
                delta_x = np.insert(delta_x, i, 0)
            delta_x[p] = 1


            B_x[B_x.index(r)] = p  # 更新入基变量索引
            N_x = list(filter(lambda x: 0 if x in B_x else 1, [i for i in range(n)]))  # 更新出基变量索引
            x_0 = [x_0[i] + lam * delta_x[i] for i in range(n)]  # 更新解
            t += 1
        #print('###########################################')


        return x_0

下面是应用单纯形法求灵敏度分析的过程：

import itertools as it
import matplotlib.pyplot as plt
plt.rcParams['font.sans-serif']=['SimHei']
plt.rcParams['axes.unicode_minus']=False


def plot(di):


    li1 = list(di.keys())
    li2 = list(di.values())
    plt.scatter([li1[i] for i in [0,80,84,100,199,291,318,355]],[li2[i] for i in [0,80,84,100,199,291,318,355]],c='r')
    # plt.text(5, 9900, s='斜率8.57', verticalalignment='bottom')
    # plt.text(11, 9970, s='斜率36.73', verticalalignment='bottom')
    # plt.text(10, 10020, s='斜率50.11', verticalalignment='bottom')
    plt.plot(di.keys(),di.values())
    # plt.xlim(-1,13)
    plt.xlabel('目标函数系数')
    plt.ylabel('最优值')
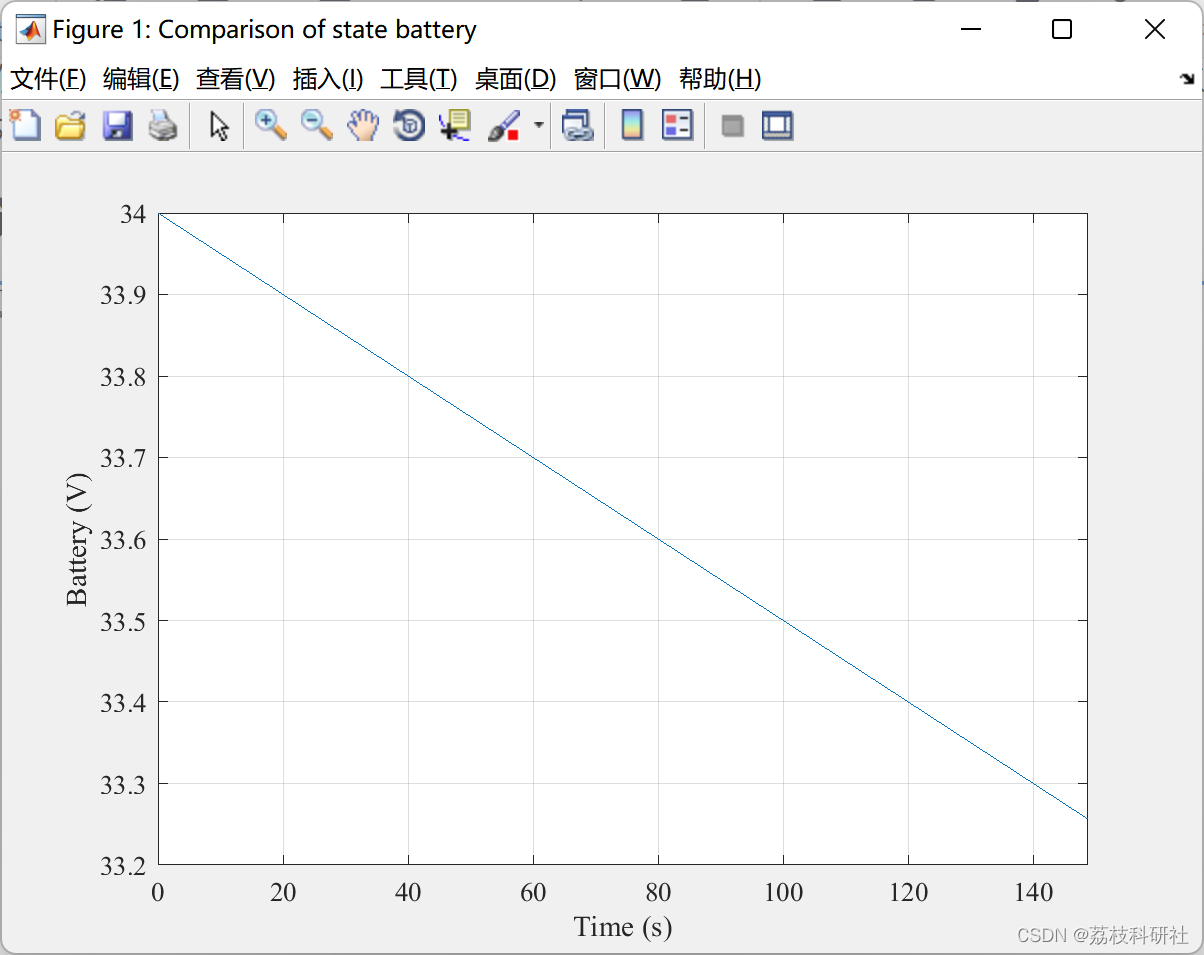
    plt.title('废料4成本对目标最优值影响')
    plt.show()




if __name__ == '__main__':
    # 系数矩阵
    A = np.array(
        [[1.000, 1.000, 1.0000, 1.000, 1, 1, 1,  0, 0,  0, 0,  0, 0,  0, 0, 0, 0],
         [0.008, 0.007, 0.0085, 0.004, 0, 0, 0, -1, 0,  0, 0,  0, 0,  0, 0, 0, 0],
         [0.008, 0.007, 0.0085, 0.004, 0, 0, 0,  0, 1,  0, 0,  0, 0,  0, 0, 0, 0],
         [0.180, 0.032, 0.0000, 0.000, 1, 0, 0,  0, 0, -1, 0,  0, 0,  0, 0, 0, 0],
         [0.180, 0.032, 0.0000, 0.000, 1, 0, 0,  0, 0,  0, 1,  0, 0,  0, 0, 0, 0],
         [0.120, 0.011, 0.0000, 0.000, 0, 1, 0,  0, 0,  0, 0, -1, 0,  0, 0, 0, 0],
         [0.120, 0.011, 0.0000, 0.000, 0, 1, 0,  0, 0,  0, 0,  0, 1,  0, 0, 0, 0],
         [0.000, 0.001, 0.0000, 0.000, 0, 0, 1,  0, 0,  0, 0,  0, 0, -1, 0, 0, 0],
         [0.000, 0.001, 0.0000, 0.000, 0, 0, 1,  0, 0,  0, 0,  0, 0,  0, 1, 0, 0],
         [1.000, 0.000, 0.0000, 0.000, 0, 0, 0,  0, 0,  0, 0,  0, 0,  0, 0, 1, 0],
         [0.000, 1.000, 0.0000, 0.000, 0, 0, 0,  0, 0,  0, 0,  0, 0,  0, 0, 0, 1],
         ])


    di = dict()
    for coef in np.linspace(0, 50, 501):
        b = np.array([1000, 6.5, 7.5, 30, 35, 10, 12, 11, 13, 75, 250])  # 常数项
        c = np.array([16, 10, 8, coef, 48, 60, 53, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0])  # 目标函数系数
        B_x = [2, 3, 4, 5, 6, 7, 10, 12, 14, 15, 16]
        # B_x = [1,7,8,9,10,11,12,13,14,15,16]
        # print(det(A[:,B_x]))
        # print(A.shape,b.shape,c.shape)
        model = Simplex(A,b,c,B_x)
        x_0 = model()
        di[coef] = np.dot(c,np.array(x_0))


    pd.DataFrame([di.keys(),di.values()]).to_csv(r'RHS.csv',index=False)
    plot(di)